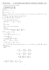Théorème (formule du binôme de Newton

Théorème (formule du binôme de Newton) :
Soit
(a; b) ∈ R2
n ∈ N.
et
On a
(a + b)n =
n X
n
k
k=0
ak bn−k
.
Démonstration :
1.
initialisation :
Pour
n = 0,
on a :
(a + b)0 = 1
et
0 X
0
k=0
2.
k
ak bn−k =
0 0 0−0
a b
= 1.
0
hérédité :
On suppose que pour un rang
n∈N
quelconque, la formule est vraie.
Montrons qu'alors elle est également vraie au rang
(a + b)n+1 =
n+1
X
k=0
n + 1,
ie que :
n + 1 k n+1−k
a b
.
k
On a :
(a + b)n+1
= (a + b)(a + b)n
n X
n k n−k
= (a + b)
a b
(par hypothèse de récurrence)
k
k=0
n n X
X
n k n−k
n k n−k
=a
a b
+b
a b
k
k
k=0
k=0
X
n n X
n
n k
k n−k
n−k
=
a×a b
+
a ×b×b
k
k
k=0
k=0
X
n n X
n k+1 n−k
n k n+1−k
=
a
b
+
a b
k
k
k=0
k=0
j = k + 1 dans la première somme, pour obtenir
X
n+1
n X n n k n+1−k
j n−(j−1)
=
a b
+
a b
j−1
k
On pose ensuite
(a + b)n+1
j=1
=
k=0
n+1
X j=1
:
n
aj bn+1−j +
j−1
n+1
X n X
n
k
k n+1−k
a b
k=0
n X
n
n k n+1−k
ak bn+1−k +
a b
(retour à l'indice k )
k−1
k
k=1
k=0
n X
n
n
=
ak bn+1−k +
an+1 bn+1−(n+1)
k−1
n+1−1
k=1
n X
n k n+1−k
n 0 n+1−0
+
a b
+
a b
(on fait en sorte que les indices
k
0
k=1
n n X
X
n
n k n+1−k
k n+1−k
n+1
n+1
=
a b
+a
+b
+
a b
k−1
k
k=1
k=1
X
n n X
n
n k n+1−k
k n+1−k
n+1
=b
+
a b
+
a b
+ an+1
k−1
k
k=1
k=1
n X
n
n
k n+1−k
n+1
=b
+
+
a b
+ an+1
k−1
k
k=1
n X
n + 1 k n+1−k
n+1
=b
+
a b
+ an+1 (triangle de Pascal)
k
k=1
n n + 1 0 n+1 X n + 1 k n+1−k
n + 1 n+1 n+1−(n+1)
a b
+
a b
+
a
b
=
0
k
n+1
k=1
n+1
X n + 1
=
ak bn+1−k
k
=
k=0
3.
conclusion :
Donc, par récurrence sur
n ∈ N,
on a le résultat.
soient les mêmes)