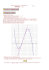EXERCICE 1 (4 points ) Commun à tous les candidats On considère

EXERCICE 1 (4 points )
Commun à tous les candidats
On considère la fonction f définie sur l’intervalle [0; +∞[ par
2
f (x) = 1 − x2 e1−x .
Son tableau de variations est le suivant :
x
0
1
1
+∞
1
f (x)
0
Sa courbe représentative C et son asymptote ∆, d’équation y = 1, sont tracées en annexe, à rendre
avec la copie.
A - Lecture graphique
1) k est un nombre réel donné. En utilisant la représentation graphique, préciser en fonction de k le
nombre de solutions dans l’intervalle [0; +∞[ de l’équation f (x) = k.
1
2) n étant un entier naturel non nul, déterminer les valeurs de n pour lesquelles l’équation f (x) =
n
admet deux solutions distinctes.
B - Définition et étude de deux suites
1)
Soit n un entier supérieur ou égal à 2. Montrer que l’équation f (x) =
un et vn respectivement comprises dans les intervalles [0; 1] et [1; +∞[.
1
admet deux solutions
n
2) Sur la feuille en annexe, construire sur l’axe des abscisses les réels un et vn pour n appartenant à
l’ensemble {2; 3; 4}.
3)
Déterminer le sens de variation des suites (un ) et (vn ).
4) Montrer que la suite (un ) est convergente et déterminer sa limite. Procéder de même pour la suite
(vn ). En déduire que les suites (un ) et (vn ) sont adjacentes.
2
ANNEXE DE L’EXERCICE 1
O
1
y
∆
1
2
C
x
A compléter et à rendre avec la copie
7
BACCALAUREAT GENERAL
Session 2004
MATHEMATIQUES
- Série S Enseignement Obligatoire
Réunion
EXERCICE 1
A - Lecture graphique
1.
Soit k un réel. Une lecture graphique nous apprend que
• si k < 0 ou k > 1, l’équation f(x) = k n’admet pas de solution dans [0, +∞[,
• si 0 < k < 1, l’équation f(x) = k admet exactement deux solutions dans [0, +∞[,
• Si k = 0 ou si k = 1, l’équation f(x) = k admet exactement une solution dans [0, +∞[.
1
1
< 1 équivaut à n > 1 ou encore n ≥ 2. Donc, l’équation f(x) =
admet deux
2. Soit n un entier naturel. 0 <
n
n
solutions distinctes si et seulement si n ≥ 2.
B - Définition et étude de deux suites
1. Soit n un entier naturel supérieur ou égal à 2.
La fonction f est continue et strictement décroissante sur l’intervalle [0, 1]. On sait alors que pour tout réel k de l’intervalle
[f(1), f(0)], l’équation f(x) = k admet une solution et une seule dans l’intervalle [0, 1]. Maintenant, f(0) = 1, f(1) = 0 et
1
1
1
puisque n est supérieur ou égal à 2, on a 0 ≤
≤ 1 ou encore f(1) ≤
≤ f(0). On en déduit que l’équation f(x) =
n
n
n
admet une et une seule solution notée un dans l’intervalle [0, 1].
De même, la fonction f est continue et strictement croissante sur [1, +∞[ et donc pour tout réel k de l’intervalle
[f(1), lim f(x)[ c’est-à-dire l’intervalle [0, 1[, l’équation f(x) = k admet une solution et une seule dans l’intervalle [1, +∞[.
x→ +∞
Comme 0 ≤
2.
1
1
< 1, l’équation f(x) =
admet une et une seule solution notée vn dans l’intervalle [1, +∞[.
n
n
Voir graphique à la fin de l’exercice.
1
1
1
1
et f(un+1 ) =
. Comme
< , on a
n
n+1
n+1
n
f(un+1 ) < f(un ). Comme f est strictement décroissante sur l’intervalle [0, 1] et que un et un+1 sont éléments de [0, 1], on
en déduit que un+1 > un .
Ainsi, pour tout entier naturel n supérieur ou égal à 2, on a un < un+1 et donc
3.
Soit n un entier naturel supérieur ou égal à 2. On a f(un ) =
la suite (un ) est strictement croissante.
De même, pour n entier naturel supérieur ou égal à 2 donné, f(vn+1 ) < f(vn ) et puisque f est strictement croissante sur
l’intervalle [1, +∞[ et que les réels vn et vn+1 sont éléments de cet intervalle, on a vn+1 < vn .
La suite (vn ) est strictement décroissante.
http ://www.maths-france.fr
1
c Jean-Louis Rouget, 2007. Tous droits réservés.
4. La suite (un ) est croissante et majorée par 1. Donc la suite (un ) est convergente. On note ℓ sa limite. Puisque, pour
tout entier naturel n, on a 0 ≤ un ≤ 1, quand n tend vers +∞, on obtient 0 ≤ ℓ ≤ 1.
1
(∗). La fonction f est continue sur [0, 1] et en particulier
Pour tout entier naturel supérieur ou égal à 2, on a f(un ) =
n
en ℓ. Par suite, quand n tend vers +∞, f(un ) tend vers f(ℓ). En faisant tendre n vers +∞ dans l’égalité (∗), on obtient
alors f(ℓ) = 0. Mais l’équation f(x) = 0 admet une solution et une seule dans [0, 1] à savoir x = 1. Par suite, ℓ = 1.
La suite (un ) est convergente et lim un = 1.
n→ +∞
De même, la suite (vn ) est décroissante et minorée par 1. Donc la suite (vn ) converge vers un réel ℓ ′ de [1, +∞[. En faisant
1
tendre n vers +∞ dans l’égalité f(vn ) = , on obtient f(ℓ ′ ) = 0 et donc ℓ ′ = 1.
n
La suite (vn ) est convergente et lim vn = 1.
n→ +∞
Ainsi,
• la suite (un ) est croissante,
• la suite (vn ) est décroissante,
• lim (vn − un ) = 1 − 1 = 0.
n→ +∞
On en déduit que
les suites (un ) et (vn ) sont adjacentes.
∆
1
C
1
2
1
3
1
4
0
0
u2 u3 u4
http ://www.maths-france.fr
1
v4
v3
2
v2
2
c Jean-Louis Rouget, 2007. Tous droits réservés.