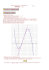Correction TES. Bac blanc .09

CORRECTION BAC BLANC DE MATHEMATIQUES
TES 2009
L’usage de la calculatrice est autorisé.
Exercice n°1 : ( 5 points ) (Commun à tous les candidats)
Questionnaire à choix multiples
Chaque question comporte trois affirmations, une seule des trois est exacte.
Une bonne réponse rapporte 1 point; une mauvaise réponse retire 0,5 point ;
l'absence de réponse donne 0 point. Si le total des points est négatif, la note globale attribuée à l’exercice est 0.
Indiquez sur votre copie le numéro de la question et recopier l’affirmation exacte sans justifier votre choix.
On considère la fonction f définie et dérivable sur ℝ .
La figure ci-dessous montre une partie de sa courbe représentative (Cf ) dans un repère orthonormal.
On dispose des renseignements suivants sur la fonction f et la courbe (Cf ) :
−
la fonction f est strictement croissante sur l’intervalle [−2 ; 2],
elle est strictement décroissante sur l’intervalle ]−∞; −2] et sur l’intervalle [2 ; +∞[ ;
−
la droite d’équation y = 0,5 est asymptote à la courbe (Cf ) en − ∞ et en + ∞ ;
−
la tangente en A  0;  à la courbe (Cf ) passe par le point de coordonnées 1;  .


1
2
 3
 2
y
Cf
1
A
O•
x
1
1) Sur ℝ , l’équation f ( x) = 0, 49 admet :
Réponse b.
a. une seule solution
b. deux solutions
c. trois solutions
2) La tangente en A à la courbe (Cf ) a pour équation :
Réponse b.
a. y = 0,5 x + 1
b. y = x + 0,5
c. y = 1,5 x + 0,5
3) Si F est une primitive de la fonction f sur ℝ alors :
Réponse a.
a. F ' ( 0 ) = 0,5
b. F est croissante sur ]−2; 0]
c. F ' ( 2 ) = 0
4) On note g la fonction définie sur [0 ; + ∞[ par g ( x ) = ln ( f ( x ) ) :
Réponse c.
a. lim g ( x) = +∞
x →+∞
b. lim g ( x) = −∞
x →+∞
c. lim g ( x) = − ln 2
x →+∞
5) On note g ' la dérivée de la fonction g sur [0 ; + ∞[ :
Réponse b.
a. g ' ( x ) =
1
f ( x)
b. g ' ( x ) =
f '( x)
f ( x)
c. g ' ( x ) =
1
f ( x ) + ln  f ' ( x ) 
x
Exercice n°2 : ( 5 points ) (Commun à tous les candidats)
La courbe C ci-contre représente une fonction f
définie et dérivable sur l’intervalle I = ]0 ; +∞[
A
•
On note f ' la fonction dérivée de f sur l’intervalle I
Les axes ( Ox ) et ( Oy ) sont asymptotes à C .
•
B
•
e
La courbe C passe par les points
1

A (1 ; 1) et B  ; 0 
e

et admet une tangente parallèle à ( Ox ) au point A.
1) En utilisant les données ci-dessus, déterminer sans justification :
f ( 1) = 1 en effet la courbe C passe par les points A (1 ; 1)
a.
et f ' ( 1) = 0 en effet au point A la tangente à la courbe C est parallèle à ( Ox ) .
b. lim f ( x ) = −∞ en effet l’axe ( Oy ) est asymptotes à C .
x→0
et lim f ( x ) = 0
x→ + ∞
en effet l’axe ( Ox ) est asymptotes à C .
1

c. L’ensemble des solutions de l’inéquation f ( x ) > 0 est  ; + ∞  C est au-dessus de ( Ox ) à partir du point B
e

l’ensemble des solutions de l’inéquation f ' ( x ) > 0 est
et
]0 ; 1[
C est strictement croissante sur
]0 ; 1[
d. Quelle est parmi les trois courbes tracées ci-dessous celle qui représente la fonction f ' ?
1,5
•
0
–0,2
3
Courbe 1
•
•
3
Courbe 2
Courbe 3
1

la Courbe 2 représente la fonction f ' car c’est la seule strictement positive uniquement sur  ; + ∞  .
e

2)
a. Quelle est parmi les trois courbes tracées ci-dessus celle qui représente une primitive F de la fonction f ?
la Courbe 3 représente la fonction F car c’est la seule croissante uniquement sur ]0 ; 1[ .
b. En déduire l’aire du domaine hachuré exprimée en unité d’aire.
e
aire = ∫ f ( x ) .dx =  F ( x )  = F ( e ) − F (1) = 1,5 − 0 = 1, 5 u.a
e
1
1
Exercice n°3 : ( 5 points ) (Commun à tous les candidats)
1
3
x + 4 + ln ( 4 x + 10 ) − 3ln x .
2
4
On appelle C la courbe ci-dessous représentative de f dans le plan muni d’un repère orthogonal.
Soit f la fonction définie sur l’intervalle ]0 ; 20] par f ( x) =
y
16
12
8
C
4
0
0
5
10
15
20
x
PARTIE A
1) Déterminer la limite de f en 0. Quelle interprétation graphique peut-on en donner ?
 1
3
3

x + 4 + ln ( 4 x + 10 )  = 4 + ln10
lim
3
1

x →0  2
4
4


lim f ( x ) = lim  x + 4 + ln ( 4 x + 10 ) − 3ln x  = +∞ par somme car 
x →0
x →0 2
4


lim ( −3 × ln x ) = +∞ car lim ln x = −∞
x →0
 x →0
alors l'axe des ordonnées est asymptote à la courbe C .
2) Montrer que pour tout x de l’intervalle ]0 ; 20], f '( x) =
x 2 − 2 x − 15
.
x ( 2 x + 5)
3
1
f = u + v − 3w
avec u ( x ) = x + 4 et v ( x ) = ln ( 4 x + 10 )
4
2
3
1
4
2
f ' = u '+ v '− 3w '
avec u ' ( x ) =
et v ' ( x ) =
=
4
2
4 x + 10 2 x + 5
x
2
x
+
5
3
4
x
+
10
(
) + 3x − (
)
1 3
2
3
f '( x ) = + ×
− =
2 4 2 x + 5 x x ( 4 x + 10 ) x ( 4 x + 10 ) x ( 4 x + 10 )
et
w ( x ) = ln x
et
w '( x) =
2 x 2 + 5 x + 3 x − 12 x − 30 2 x 2 − 4 x − 30 x 2 − 2 x − 15
=
=
=
x ( 2 x + 5)
x ( 4 x + 10 )
2 x ( 2 x + 5)
3) Déterminer les variations de la fonction f sur l’intervalle ]0 ; 20] et dresser son tableau de variations.
Sur l’intervalle ]0 ; 20] , f ' ( x ) est du signe du trinôme au numérateur : x 2 − 2 x − 15
donc f ' ( x ) est positif à l’extérieur des racines x1 =
d’où le tableau des variations de f :
2 − 64
= −3
2
et
x2 =
2 + 64
=5
2
1
x
x
0
f '( x )
α
5
–
0
β
+
f ( 20 )
+∞
f ( x)
20
6
6
f ( 5)
On admet que l’équation f (x) = 6 possède exactement deux solutions α et β dans l’intervalle ]0 ; 20]
telles que α ≈ 1,242 et β ≈ 13,311.
PARTIE B
Une entreprise produit au maximum 20 000 objets par jour.
On note x le nombre de milliers d’objets produits chaque jour travaillé : x ∈]0 ; 20].
On admet que le coût moyen de fabrication, exprimé en euros, d’un objet, lorsqu’on en a produit x milliers,
est égal à f (x), où f est la fonction définie ci-dessus.
1)
a. Pour combien d’objets produits le coût moyen de fabrication est-il minimal ?
D'après le tableau des variations, le minimum de la fonction f est atteint pour x = 5
Le coût moyen de fabrication est donc minimal pour une production de 5000 objets.
b. Déterminer ce coût moyen minimal, arrondi au centime.
1
3
13 3
f ( 5 ) = = × 5 + 4 + ln ( 4 × 5 + 10 ) − 3ln 5 = + ln 30 − 3ln 5 ≃ 4, 22
2
4
2 4
Le coût moyen minimal de fabrication est 4,22 €.
2) Le prix de vente d’un objet est 6 €. Pour quelles productions journalières l’entreprise réalise-t-elle un bénéfice ?
L’entreprise réalise un bénéfice quand le coût moyen de fabrication est inférieur au prix de vente d'un objet.
Par hypothèse, l’équation f ( x ) = 6 possède exactement deux solutions α et β dans l’intervalle ]0 ; 20]
telles que α ≈ 1,242 et β ≈ 13,311.
Sur ]0 ; 5] la fonction f est strictement décroissante donc si α < x ≤ 5 alors f ( x ) < 6
Sur [5 ; 2] la fonction f est strictement croissante
donc si 5 ≤ x < β alors f ( x ) < 6
L’entreprise réalise donc un bénéfice pour une production x appartenant à l’intervalle ]α ; β [
D'autre part, f (1, 242 ) > 6 et
f (13,311) < 6
Donc l’entreprise réalise un bénéfice pour toute production comprise entre 1 243 et 13 311 objets par jour.
3) Déterminer le bénéfice journalier, arrondi à la centaine d’euros, pour une production de 5 000 objets par jour.
Le montant du bénéfice pour une production de 5 000 objets par jour est : 5000 × ( 6 − 4, 22 ) = 8900
En admettant, que toute la production est vendue, le bénéfice journalier de l'entreprise est de 8900 €.
4) L’année suivante, le coût moyen augmente de 2%. Le prix de vente est alors augmenté de 2%.
Le bénéfice journalier reste-t-il identique ? Justifier.
Dans cette question, toute trace de recherche, même incomplète, sera prise en compte dans l’évaluation.
Le coefficient multiplicateur associé à une augmentation de 2% est 1,02.
La fonction g définie sur l’intervalle ]0 ; 20] par g ( x ) = 1, 02 × f ( x ) a les mêmes variations que la fonction f .
En particulier, le minimum de la fonction g est atteint pour x = 5 et g ( 5 ) = 1, 02 × f ( 5 )
Le montant du bénéfice pour une production de 5 000 objets par jour est alors :
5000 × (1, 02 × 6 − 1, 02 × 4, 22 ) = 5000 × 1, 02 × ( 6 − 4, 22 ) = 1, 02 × 8900
En admettant, que toute la production est vendue, le bénéfice journalier de l'entreprise augmente de 2%.
Exercice n°4 : ( 5 points ) (Réservé aux candidats n’ayant pas suivi l’enseignement de spécialité)
PARTIE A
Soit g la fonction définie par :
g : [ 2 ; 20] → ℝ
x
֏ g ( x ) = x − 2 − 2ln ( x )
1) Etudier les variations de la fonction g puis dresser son tableau de variation.
g = u − 2v
avec u ( x ) = x − 2
et
v ( x ) = ln x
g ' = u '− 2v '
avec u ' ( x ) = 1
et
v '( x) =
1
x
2 x−2
=
sur l’intervalle [ 2 ; 20] comme x ≥ 2 , on a g ' ( x ) ≥ 0
x
x
d’où le tableau des variations de g :
g '( x ) = 1 −
x
g '( x)
α
2
20
+
18 − 2 ln 20 ≃ 12
g ( x)
0
−2 ln 2
2) Montrer que la fonction g s’annule exactement une fois sur l’intervalle [ 2 ; 20] .
Indiquer la valeur arrondie à une décimale de ce nombre.
D’après le tableau de variation de g comme g ( 2 ) < 0 et g ( 20 ) > 0 la fonction g s’annule exactement une
fois sur l’intervalle [ 2 ; 20] , à la calculatrice je trouve :
5,35 < α < 5,36 ainsi α ≃ 5, 4 .
3) En déduire le signe de la fonction g sur l’intervalle [ 2 ; 20] et récapituler ces résultats dans un tableau.
D’après le tableau de variation, on a :
x
2
α
0
–
g ( x)
20
+
PARTIE B
Soit G la fonction définie par :
G : [ 2 ; 20] → ℝ
x
֏ G ( x) =
1 2
x − 2 x ln ( x )
2
1) Montrer que G est une primitive de g sur [ 2 ; 20] .
1
G = u − 2v.w
avec u ( x ) = x 2
et v ( x ) = x
et w ( x ) = ln x
2
1
1
G ' = u '− 2 ( v '.w + v.w ' )
avec u ' ( x ) = 2 x
et v ' ( x ) = 1
et w ' ( x ) =
2
x
1
1

G ' ( x ) = × 2 x − 2  ln x + x ×  = x − 2 ( ln x + 1) = x − 2 − 2 ln x = g ( x ) donc G est une primitive de g .
2
x

2) Soit I le nombre défini par : I = ∫ g ( x ) dx
20
16
a. Exprimer le nombre I uniquement à l’aide de nombres entiers et des deux nombres ln 2 et ln 5 .
20
1
1

I = ∫ g ( x ) dx = G ( x ) 16 = G ( 20 ) − G (16 ) = × 20 2 − 40 ln 20 −  × 16 2 − 32 ln16  = 72 − 40 ln ( 2 2 × 5 ) + 32 ln ( 24 )
16
2
2

I = 72 − 40 ( 2 ln 2 + ln 5 ) + 32 ( 4 ln 2 ) = 72 − 80ln 2 − 40 ln 5 + 128ln 2 ≃ 72 + 48 ln 2 − 40 ln 5 u.a
20
b. Donner la valeur de I arrondie à deux décimales.
I ≃ 40, 89 u.a