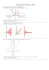a = 1 a = 1 1 u

Solution – Arithmétique – Congruences – Suites Numériques – s5067
On considère la fonction f définie sur IR – {4} par f(x) =
x2 – 7x + 14
.
x–4

→

→
On note Cf sa courbe représentative dans un repère (O ; i ; j ) du plan.
1/ Déterminer les réels a , b , c tels que, pour tout x de IR – {4} , f(x) = ax + b +
a)
c
.
x–4
c
(ax + b)(x – 4) + c ax2 + (b – 4a)x + (c – 4b)
=
=
.
x–4
x–4
x–4
Procédons par identification : f(x) = ax + b +
On identifie les deux écritures de f(x) (même coefficient pour chaque puissance de x ).
a=1
a=1
2
b
–
4a
=
-7
⇒  b = -3 , soit f(x) = x – 3 +
.

x
–
4
 c – 4b = 14
c=2
b) Autre méthode (en forçant la factorisation du dénominateur x – 4 ) :
f(x) =
2
x2 – 7x + 14 x(x – 4) – 3x + 14 x(x – 4) – 3(x – 4) + 2
=
=
=x–3+
.
x–4
x–4
x–4
x–4
2/ Etudier les limites de f aux bornes de son domaine de définition.
Si x → 4- , alors x – 3 → 1 (inutile de préciser 1- ou 1+ , car non nul) et x – 4 → 0- , soit
2
→ -∞ .
x–4
On déduit, après addition : lim – f(x) = -∞ .
x →4
Si x → 4+ , alors x – 3 → 1 et x – 4 → 0+ , soit
2
→ +∞ . On déduit : lim + f(x) = +∞ .
x–4
x →4
Existence d’une asymptote verticale.
Si x → -∞ , x – 3 → -∞ et
Si x → +∞ , x – 3 → +∞ et
2
→ 0 , soit, après addition : lim f(x) = -∞ .
x–4
x → -∞
2
→ 0 , soit
x–4
lim f(x) = +∞ .
x → +∞
3/ En déduire l’existence d’une asymptote verticale (d1) à la courbe Cf , et donner son équation.
On a vu l’existence de d’une asymptote verticale d’abscisse x = + 4 , soit d1 : x = 4 .
4/ Etudier les variations de f .
f , somme et rapport de polynômes, est définie, continue et dérivable sur IR – {4} .
On sait que
2
1' = - u’2 , d’où : f(x) = x – 3 + 2 ⇒ f’(x) = 1 – 2 2 = (x – 4) –2 2 = (x – 4 – 2)(x –2 4 + 2) .
x–4
(x – 4)
(x – 4)
(x – 4)
u u
On peut aussi utiliser
f’(x) =
2
2
u' = u’v –2 v’u , soit f(x) = x – 7x + 14 ⇒ f’(x) = (2x – 7)(x – 4) – 1(x2 – 7x + 14) ,
v
x–4
(x – 4)
v 
x2 – 8x + 14
, de racines x1 = 4 – 2 et x2 = 4 + 2 .
(x – 4)2
Les extrema sont :
E1 d’abscisse x1 = 4 – 2 , d’ordonnée y1 = f(x1) = (4 – 2) – 3 +
2
2
=1– 2–
=1–2 2,
(4 – 2) – 4
2
E2 d’abscisse x1 = 4 + 2 , d’ordonnée y1 = f(x1) = (4 + 2) – 3 +
2
2
=1+ 2+
=1+2 2.
(4 + 2) – 4
2
1
La dérivée f’(x) est du signe de (x – 4 – 2)(x – 4 + 2) = x2 – 8x + 14 .
Tableau de variation :
x
-∞
f '(x)
f (x)
+
0
-∞
–
x → -∞
∞
2
= 0 et
x
–
4
→ -∞
lim [f(x) – (x – 3)] = lim
x
||
+∞
-4 + 2
||
-∞
-1 – 2 2
5/ Démontrer que lim [f(x) – (x – 3)] = 0 et
x → -∞
-4
-4 – 2
–
+∞
0
+
+∞
-1 + 2 2
lim [f(x) – (x – 3)] = 0 . Comment interpréter ces résultats.
x → +∞
∞
2
=0.
x
–
4
→ +∞
lim [f(x) – (x – 3)] = lim
x → +∞
x
L’écart algébrique entre Cf et d2 : y = x – 3 devient nul aux infinis, donc (d2) est asymptote oblique à Cf .
6/ Etudier les positions relatives de la courbe Cf et de la droite (d2) d’équation y = x – 3 .
On étudie le signe de l’écart algébrique vertical entre Cf et (d2) , soit E(x) = f(x) – (x – 3) =
2
.
x–4
 x < 4 : E(x) < 0 ⇔ f(x) – (x – 3) < 0 ⇔ Cf sous (d2)
E(x) est du signe de x – 4 , soit :  x > 4 : E(x) > 0 ⇔ f(x) – (x – 3) > 0 ⇔ C au dessus de (d ) .

f
2
7/ Tracer les courbes Cf , (d1) et (d2) dans le repère précédent.
On pourrait montrer que I(4 ; 1) , intersection des asymptotes, est centre de symétrie de Cf .
y
6
5
4
Cf
3
2
d2 : y = x - 3
1
-4
-3
-2
-1
0
1
2
3
4
5
-1
d1 : x = 4
-2
-3
-4
-5
-6
2
6
7
8
9
10x