f ( ) = f x k (avec ∈» ( ) ′ = f x 0 ( ) = + f x mx p (avec ≠ ( ) ′ = f x m
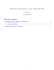
Transcription
f ( ) = f x k (avec ∈» ( ) ′ = f x 0 ( ) = + f x mx p (avec ≠ ( ) ′ = f x m
Site : http://francois.schulhof.perso.neuf.fr/cours_maths/ Page 1 _FICHE : Chapitre DERIVATION d’une fonction__ I) Taux de variation d’une fonction f sur un intervalle I Le taux de variation d’une fonction f entre a et b=a+h est le nombre T tel que f (b) - f (a ) f (a + h) - f (a) = avec h ¹ 0 b-a h T = ( Remarque : si h < 0 alors a+h < a ) Interprétation graphique de ce nombre T : c’est la pente de la droite (AB) qui est appelée une sécante à la courbe C f avec le point A de coordonnées : ( a ; f(a) ) et B :( b ; f(b) ) ou ( a+h ; f(a+h) ) II) Nombre dérivé d’une fonction f en a SI lim h®0 f ( a + h) - f ( a ) h existe (Î ¡ ) ALORS on POSE lim h ®0 f (a + h) - f (a) = f ¢(a) h ET on dit que la fonction f est dérivable en a Et si pour tout nombre a appartenant à un intervalle I la fonction f est dérivable en a on dit que la fonction f est dérivable sur l’intervalle I et on définit sur cet intervalle I une nouvelle fonction qui s’appelle « fonction dérivée de f » et qui est notée f’ III) Equation de la tangente à une courbe en un point si f est dérivable en a : L’équation de la tangente à la courbe C f au point d’abscisse a est : y = f ¢(a) ( x - a) + f (a) ( la tangente est la limite des sécantes (AB) à la courbe quand B tend vers A ) IV) Fonctions dérivées des fonctions usuelles D f est le domaine de définition de la fonction f et D f ¢ est le de dérivabilité de la fonction f fonction f définie par Df fonction dérivée f’ définie par Df ¢ f ( x) = x 2 ¡ ¡ ¡ f ¢( x ) = 0 f ¢( x) = m f ¢( x) = 2x ¡ ¡ ¡ f ( x) = x 3 ¡ f ¢( x ) = 3x 2 ¡ f ( x) = x n (avec n Î N ) ¡ f ¢( x) = nx n-1 ¡ 1 = x -1 x 1 f ( x) = = x -2 2 x ¡* f ¢( x) = ( -1) x -2 = f ( x ) = k (avec k Î ¡ ) f ( x) = mx + p (avec m ¹ 0 ) f ( x) = f ( x) = x = f ( x) = 1 x = ¡* 1 x2 ¡+ -1 x2 ¡ +* f ( x) = x q (avec q Î ¤ ) ¡ +* -1 f ¢( x) = ( -2) x -3 = f ¢( x) = f ¢( x) = 1 2 1 -1 x2 f ¢( x) = qx q -1 x -2 x ¡* 3 -1 = -1 -1 2 -1 x 2 ¡* 2 1 2 1 x = 2 2 x = -3 -x 2 2 = -1 ¡ +* ¡ +* 3 2x 2 ¡ +* Site : http://francois.schulhof.perso.neuf.fr/cours_maths/ Page 2 V) Opérations sur les fonctions dérivables Soit u et v 2 fonctions dérivables en x0 Î ¡ alors la fonction u + v est dérivable en x0 ET les fonctions ku et u ´ v sont dérivables en x0 . ET la fonction Valeur de la fonction f en x0 1 u est dérivable en x0 si u ( x0 ) ¹ 0 Valeur de la fonction dérivée de f en x0 Opération f ( x0 ) = (u + v )( x0 ) = u ( x0 ) + v ( x0 ) f ¢( x0 ) = ku ¢( x0 ) f ¢( x0 ) = u¢( x0 ) + v '( x0 ) (ku )¢ = ku ¢ (u + v )¢ = u ¢ + v ' f ( x0 ) = (u ´ v)( x0 ) = u ( x0 ) ´ v( x0 ) f ¢( x0 ) = u¢( x0 )v( x0 ) + u ( x0 )v '( x0 ) (uv)¢ = u ¢v + uv ' u ( x0 ) æuö f ( x0 ) = ç ÷ ( x0 ) = avec v( x0 ) ¹ 0 v ( x0 ) èvø f ¢( x0 ) = f ( x0 ) = ku ( x0 ) f ( x0 ) = (avec k Î ¡ ) 1 avec u ( x0 ) ¹ 0 u ( x0 ) f ¢( x0 ) = æ u ö¢ u ¢v - uv ' ç ÷ = v2 èvø u ¢( x0 )v( x0 ) - u ( x0 )v '( x0 ) v 2 ( x0 ) -u ¢( x0 ) u 2 æ 1 ö¢ -u ¢ ç ÷ = 2 èuø u ( x0 ) VI) Dérivation d’une fonction « composée » de 2 fonctions Soit u une fonction dérivable en x0 Î Du et f une fonction dérivable en u ( x0 ) Î D f alors la fonction « composée » définie par g = f o u est dérivable en x0 On a : g ( x ) = ( f o u )( x ) = f éë u ( x ) ùû ( et ) g¢ ( x ) = ( f o u )¢ ( x ) = f éë u ( x ) ùû ¢ = f ¢ éë u ( x )ùû ´ u¢ ( x ) fonctions f ou g définies par D f ou Dg fonctions dérivées f’ ou g’ définies par D f ¢ ou Dg ¢ ¡ f ¢( x) = 2x ¡ Du g ¢( x ) = 2 ´ u ( x ) ´ u¢ ( x ) Du f ( x) = x n (avec n Î N ) n g ( x) = ( u ( x ) ) ¡ f ¢( x) = nx n-1 ¡ Du g ¢( x ) = n ( u ( x ) )n-1 ´ u¢ ( x ) Du g ( x) = u q ( x ) Du et ??? g ¢( x ) = q ( u ( x ) )q -1 ´ u¢ ( x ) Du et ??? Du g ¢( x ) = 3 ´ u3-1 ( x ) ´ u ¢ ( x ) = 3 ´ u 2 ( x ) ´ u ¢ ( x ) Du et g ¢( x ) = ( -1) ´ u -1-1 ( x ) ´ u ¢ ( x ) = f ( x) = x 2 g ( x ) = éëu ( x ) ùû 2 avec q Τ g ( x) = u 3 ( x ) g ( x) = 1 = u -1 ( x ) u ( x) g ( x) = u ( x ) = u æ1ö ç ÷ è2ø u (x ) ¹ 0 Du et ( x) u (x ) ³ 0 -u ¢ ( x ) u2 x ( ) æ1 ö -1÷ u¢( x ) 1 ç g ¢( x ) = uè 2 ø ( x ) ´ u ¢ ( x ) = 2 2 u ( x) Du Du et u (x ) ¹ 0 Du et u (x ) > 0 Site : http://francois.schulhof.perso.neuf.fr/cours_maths/ Page VII) Tableau de variation de la fonction f en fonction du signe de f ¢ L’étude du signe de la fonction f ¢ permet une étude des variations (croissance ou décroissance) de la fonction f sur des intervalles I définis sur ¡ Ì D f et permet de tracer le TABLEAU DE VARIATION de la fonction f Propriétés : Ø Si f '( x0 ) > 0 alors f est strictement croissante sur un voisinage de x0 Ø Si f '( x0 ) < 0 alors f est strictement décroissante sur un voisinage de x0 Ø Si f '( x0 ) = 0 alors C f admet une tangente horizontale au point d’abscisse x0 VIII) Autres notions à comprendre et à retenir : 1 ) Recherche des points appelés des « extremum locaux » à une courbe Cf Définition : Le point A de coordonnées ( a ; f(a) ) est appelé « minimum local » si et seulement si f ( a) £ f ( x ) sur un voisinage de a Le point A de coordonnées ( a ; f(a) ) est appelé « maximum local » si et seulement si f ( a) ³ f ( x ) sur un voisinage de a Propriété : Si la fonction f est une fonction dérivable et « est définie autour de a » alors : le point A de coordonnées ( a ; f(a) ) est un « extremum local » si et seulement si f ¢(a) = 0 (. tangente horizontale ) et si f ¢( x ) change de signe en a ( changement de monotonie )__ Remarque n° 1 : si a Î ¡ est une borne de D f alors on considère que le point A de coordonnées ( a ; f(a) ) est un « extremum local » à la courbe C f quel que soit f ¢ Remarque n° 2 : si f ¢( a) = 0 et si f ¢( x ) ne change pas de signe en a alors le point A de coordonnées ( a ; f(a) ) est appelé un « point d’inflexion » ( la tangente traverse la courbe C f ) 2 ) Notion de « convexité ou de concavité » d’une fonction f sur un intervalle I Soit une fonction f 2 FOIS DERIVABLES sur un intervalle I donné Ì D f Propriété : ( propriété étudiée en classe de Terminale ) Ø Si f ¢¢( x) ³ 0 sur I alors la fonction f est une fonction convexe sur l’intervalle I La courbe C f est « au-dessus » de toutes les tangentes à C f sur l’intervalle I Commentaire : On dit que la courbe C f est orientée vers « le haut » Ø Si f ¢¢( x) £ 0 sur I alors la fonction f est une fonction concave sur l’intervalle I La courbe C f est « au-dessous » de toutes les tangentes à C f sur l’intervalle I Commentaire : On dit que la courbe C f est orientée vers « le bas » 3