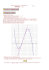DS derivation

1S1 : DEVOIR SURVEILLÉ N°4 (1 heure)
Exercice 1 (3 points)
y
Ci-contre est donnée la courbe C¦ représentant
une fonction ¦ définie et dérivable sur
9
l'intervalle [1 ; 8].
1. Par
lecture
graphique,
donner,
sans
C¦
justifier, la valeur de : ¦(3) ; ¦'(3) ; ¦(6)
2
et ¦'(6).
O
2. Le graphique ne permet pas la lecture de
¦'(4). Préciser
néanmoins son
3
1
6
signe.
(Expliquer)
Exercice 2 (9 points)
On considère la fonction ¦ définie sur  par : ¦(x) = x 3 - 3x - 3. On note C¦ sa représentation graphique.
1. Étudier les limites de ¦ en -¥ et en +¥.
2. Calculer la dérivée ¦' de ¦.
3. Dresser le tableau de variations de la fonction ¦.
4. Déterminer une équation de la tangente T à C¦ au point d'abscisse 0.
5. Tracer T et C¦ (dans un même repère). (On se limitera à l'intervalle [-2 ; 2,5] et on choisira 2 cm par unité sur chaque axe)
6. Démontrer que l'équation ¦(x) = 0 admet une unique solution a dans l'intervalle [2 ; 3].
Donner une valeur approchée de a, par défaut, à 10-1 près.
Exercice 3 (6 points)
Un fermier décide de réaliser un poulailler (en forme rectangulaire) le long du mur de sa maison. Ce poulailler
devra avoir une aire de 392 m2. Où doit-on placer les piquets A et B pour que la longueur de la clôture soit
minimale ?
mur de la ferme
x
A
x
B
y
La figure ci-dessus représente le poulailler accolé à la ferme en vue de dessus. On appelle x la distance séparant
chaque piquet au mur et y la distance entre les 2 piquets A et B. (On a donc x > 0 et y > 0)
DS 4 - 1S - Dérivation
Page 1
G. COSTANTINI http://bacamaths.net/
8
x
1. Sachant que l'aire du poulailler est 392 m2, exprimer y en fonction de x.
392
.
x
3. Calculer la dérivée l' de l. En déduire le tableau de variation de l.
2. Démontrer que la longueur l(x) du grillage est : l(x) = 2x +
4. En déduire les dimensions x et y pour lesquelles la clôture a une longueur minimale. Préciser cette longueur.
Exercice 4 (2 points)
Soient ¦ et g deux fonctions dérivables sur l'intervalle I = [0 ; 1] telles que : ¦(0) = g(0) et ¦' g' sur I.
Démontrer que ¦  g sur I. (On pourra étudier les variations de g - ¦)
DS 4 - 1S - Dérivation
Page 2
G. COSTANTINI http://bacamaths.net/
1S1 : DEVOIR SURVEILLÉ N°4 : CORRIGÉ
Exercice 1 (3 points)
y
1. ¦(3) = 9 (Image de 3)
¦(6) = 2 (Image de 2)
9
¦'(3) = 0 (Tangente horizontale)
¦'(6) = 0 (Idem)
C¦
2. La fonction ¦ est strictement décroissante sur
2
l'intervalle [3 ; 6] donc ¦'(4) < 0.
O
3
1
6
x
8
Exercice 2 (9 points)
On considère la fonction ¦ définie sur  par : ¦(x) = x 3 - 3x - 3. On note C¦ sa représentation graphique.
1. ¦ est une fonction polynôme de degré 3. Sa limite en -¥ (et en +¥) est donnée par la limite de son terme de
plus haut degré : lim ¦(x) = lim x 3 = -¥ et
x ® -¥
x ® -¥
lim ¦(x) = lim x 3 = +¥.
x ® +¥
x ® +¥
¦'(x) = 3 x 2 - 3 = 3( x 2 - 1) = 3(x - 1)(x + 1)
2. On a immédiatement :
3. La dérivée ¦' est une fonction polynôme de degré 2. Son signe est celui de a (coefficient de x 2 ) sauf entre
les racines. Ici, a = 3 et les racines sont -1 et 1. Donc ¦' est positive sauf entre -1 et 1. On en déduit le
tableau de variation de ¦ :
x
–¥
–1
Signe de la
dérivée ¦ '
+
0
1
-
0
+¥
+
-1
+¥
Variations de ¦
-¥
-5
y
Maximum local (ou relatif) en -1 : ¦(-1) = (-1)3 - 3´(-1) - 3 = -1
Minimum local (ou relatif) en 1 :
2
T
C¦
¦(1) = 13 - 3 - 3 = -5
1
4. Une équation de la tangente T à C¦ au point d'abscisse x0 est donnée par la formule :
y = ¦(x0) + ¦'(x0)(x - x0)
-2
Lorsque x0 = 0, la formule devient :
-1
O
1
-1
y = ¦' (0) x + ¦(0)
Et comme ¦(0) = -3 et ¦' (0) = -3, on obtient :
T : y = -3x - 3
5. Représentation graphique de T et C¦ (dans un même repère) :
6. La fonction ¦ est continue (puisque dérivable) sur  donc a fortiori sur [2 ; 3].
La fonction ¦ est strictement croissante sur [2 ; 3].
¦(2) = -1 < 0 et ¦(3) = 15 > 0. (Signes contraires)
DS 4 - 1S - Dérivation
Page 3
-5
G. COSTANTINI http://bacamaths.net/
2
a
x
L'équation ¦(x) = 0 admet donc une unique solution a dans l'intervalle [2 ; 3].
Localisation de a :
x
2,1
2,2
2,3
2,4
¦(x)
-0,039
1,048
2,267
...
Comme ¦(2,1) < 0 et ¦(2,2) > 0, on a :
2,5
2,6
2,7
2,8
2,9
2,1 < a < 2,2.
Une valeur approchée de a, par défaut, à 10-1 près est donc : a  2,1.
Exercice 3 (6 points)
mur de la ferme
x
392 m2
A
y
x
B
1. Puisque l'aire du poulailler est 392 m2 on a : xy = 392 d'où : y =
2. La longueur l(x) du grillage est :
3. La fonction l est du type l = u +
l'(x) = 2 -
l(x) = 2x + y = 2x +
392
.
x
392
x
ìu ( x ) = 2 x
392
v¢
avec í
. Donc l' = u' - 2 , ce qui donne :
v
v
î v( x ) = x
392
x
2
=
2 x 2 - 392
x
2
=
2( x 2 - 196)
x
2
=
2( x - 14)( x + 14)
x2
Comme x > 0, le signe de l' ne dépend que de celui de x - 14 :
x
0
14
+¥
Signe de x - 14
-
Signe de x + 14
+
+
+
+
Signe de x2
0
Signe de la dérivée l '
-
0
0
+¥
+
+
+¥
Variations de l
56
Minimum local (ou relatif) de l en 14 :
l(14) = 56
4. La clôture a une longueur minimale lorsque x = 14 et y =
Cette longueur minimale est l(14) = 56.
DS 4 - 1S - Dérivation
Page 4
392
= 28.
14
G. COSTANTINI http://bacamaths.net/
Exercice 4 (2 points)
Calculons la dérivée de la fonction g - ¦ : (g - ¦)' = g' - ¦'.
Comme ¦' g' sur I, on a : g' - ¦'  0 sur I. La fonction g - ¦ est donc croissante sur I. Ce qui signifie :
pour tous réels u et v de I : u < v Þ (g - ¦)(u)  (g - ¦)(v)
C'est-à-dire :
pour tous réels u et v de I : u < v Þ g(u) - ¦(u)  g(v) - ¦(v)
En particulier avec u = 0, on a :
pour tout v de I : g(0) - ¦(0)  g(v) - ¦(v)
Et comme ¦(0) = g(0) :
pour tout v de I : 0  g(v) - ¦(v)
C'est-à-dire :
pour tout v de I : 0  g(v) - ¦(v)
Ce qui signifie :
DS 4 - 1S - Dérivation
¦  g sur I
Page 5
G. COSTANTINI http://bacamaths.net/