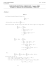Fonctions continues et uniformement continues

Transcription

FONCTIONS NUMÉRIQUES DÉFINIES SUR UN INTERVALLE
CONTINUITÉ, CONTINUITÉ UNIFORME. APPLICATIONS
SOMMAIRE
SOMMAIRE
1. Continuité
2
1.1. Définition de la continuité en un point
2
1.2. Caractérisation de la continuité par les suites. Exemple : x a sin 1
x
ne peut pas se prolonger par continuité en 0
2
1.3. Définition de la continuité sur un intervalle
3
1.4. Théorème des valeurs intermédiaires
3
1.5. Corollaire : image d'un intervalle par une application continue
5
2. Continuité uniforme
5
2.1. Définition de la continuité uniforme sur un intervalle. Exercice : si ¦ est u-continue, elle admet une limite finie 5
2.2. Théorème : les fonctions lipschitziennes sont uniformément continues
6
2.3. CNS pour qu'une fonction dérivable soit lipschitzienne.
8
2.4. Théorème de Heine. Exercice : si ¦ continue sur [a, +¥[ admet une limite finie en +¥, alors ¦ est u-continue
8
3. Applications
10
3.1. Une fonction continue sur un segment est bornée et atteint ses bornes
10
3.2. Théorème du point fixe
11
3.3. Sommes de Riemann
14
3.4. Approximation d'une fonction continue sur un segment par des fonctions en escalier
17
4. Annexe : étude de quelques fonctions usuelles
Continuité, u-continuité. Applications
18
Page 1
G. COSTANTINI http://bacamaths.net/
1. Continuité
1.1. Définition
Soient ¦ une fonction définie sur un intervalle I et a Î I.
On dit que ¦ est continue en a lorsque :
"e Î  *+ , $h Î  *+ , "x Î I, (|x - a|  h Þ |¦(x) - ¦(a)|  e)
Cette définition revient à dire :
¦ continue en a Û ¦ admet une limite en a égale à ¦(a)
1.2. Théorème Caractérisation de la continuité par les suites
Soient ¦ une fonction définie sur un intervalle I et a Î I.
Les deux assertions suivantes sont équivalentes :
(i) ¦ continue en a
(ii) Pour toute suite (xn) d'éléments de I : lim xn = a Þ
n ® +¥
lim ¦(xn) = ¦(a)
n ® +¥
Démonstration
(i) Þ (ii)
Supposons ¦ continue en a. Soit (xn) une suite d'éléments de I. Soit e Î  *+ .
Comme ¦ est continue en a, on a:
$h Î *+ tel que : (|x - a|  h Þ |¦(x) - ¦(a)|  e)
Mais la suite (xn) converge vers a. Donc pour ce réel h ci-dessus, on peut trouver N Î  tel que :
n  N Þ |xn - a|  h
On a donc, par transitivité des implications :
n  N Þ |¦(xn) - ¦(a)|  e
Ceci prouve que la suite (¦(xn)) converge vers ¦(a).
(ii) Þ (i)
Raisonnons par contraposition et montrons : non (i) Þ non (ii).
Supposons ¦ non continue en a.
Construisons une suite (xn) d'éléments de I qui converge vers a sans que la suite (¦(xn)) converge vers ¦(a).
Puisque ¦ n'est pas continue en a :
$e Î  *+ , "h Î  *+ , $x Î I, (|x - a|  h et |¦(x) - ¦(a)| > e)
En particulier avec h =
1
(n Î *), il existe xn dans I tel que :
n
1
|xn - a| 
et |¦(xn) -¦(a)| > e
n
La suite (xn) ainsi définie converge vers a (par encadrement) et la suite (¦(xn)) ne converge pas vers ¦(a)
(puisque l'écart |¦(xn) -¦(a)| est minoré par un réel strictement positif)
Par contraposition, on obtient l'implication souhaitée.
D'où le théorème.
Page 2
Remarque : ce théorème est faux si a Î I \ I. Considérer, par exemple, la fonction "partie entière" sur I = [0, 1[
1
avec a = 1 et la suite (xn) définie par xn = 1 - . Cette suite tend vers 1, mais la suite (E(xn)) étant nulle sa
n
limite est 0 ¹ E(1).
1
1
Il se peut même que la suite (¦(xn)) diverge : prendre ¦ : x Î ]0 ; 1] a
et la suite (xn) : n Î * a
.
x
n
Cependant, nous verrons plus loin que si ¦ est uniformément continue, la convergence de (xn) vers une borne de
I entraîne celle de (¦(xn)).
Exemple :
Soit l Î [-1, 1].
ì 1
ïsin si x ¹ 0
¦(x) = í x
ï l si x = 0
î
Soit ¦ la fonction définie sur  par :
Démontrer que ¦ n'est pas continue en 0.
On considère les deux suites (un) et (vn) définies par :
un =
1
et vn =
p
+ 2np
2
1
-
p
+ 2np
2
lim un = lim vn = 0
On a :
n ® +¥
Or, ¦(un) = 1 et ¦(vn) = -1 donc lim ¦(un) = 1 et
n ® +¥
n ® +¥
lim ¦(vn) = - 1
n ® +¥
Si ¦ était continue en 0, on devrait avoir :
lim ¦(un) = ¦(0)
n ® +¥
1=l
C'est-à-dire :
De même, on devrait avoir :
C'est-à-dire :
lim ¦(vn) = ¦(0)
n ® +¥
-1 = l
D'où une contradiction.
Donc ¦ n'est pas continue en 0.
1.3. Définition
Soit ¦ une fonction définie sur un intervalle I. On dit que ¦ est continue sur I lorsque :
"a Î I, ¦ est continue en a
Notons que la continuité (simple) est une notion locale (chaque h de la définition 1.1. est dépendant de a)
1.4. Théorème des valeurs intermédiaires
Soit I un intervalle. Soient a et b dans I.
Soit ¦ une application continue sur l'intervalle I et à valeurs dans .
Soit l un réel compris entre ¦(a) et ¦(b).
Il existe c dans [a, b] tel que : ¦(c) = l.
Page 3
Démonstration :
Déjà, si ¦(a) = ¦(b) alors nécessairement l = ¦(a) = ¦(b) et le théorème est vrai en choisissant c = a ou c = b.
Dans toute la suite, on peut donc supposer : ¦(a) < ¦(b). (Quitte à poser g = -¦ si ¦(a) > ¦(b)).
Notons :
X = {x Î [a, b] tels que ¦(x)  l}
Cet ensemble X est non vide. En effet, ¦(a)  l, donc a Î X.
Cet ensemble X est majoré par b (puisque X est un sous ensemble de [a, b]).
Donc X admet une borne supérieure c. (Et c Î [a, b])
Montrons que ¦(c)  l :
Comme c = sup X, il existe une suite (xn) d'éléments de X qui converge vers c.
¦(xn)  l
Comme les xn sont dans X, on a :
Or, ¦ est continue en c, donc par passage à la limite :
¦(c)  l
Montrons que ¦(c)  l :
Déjà, si c = b alors ¦(c) = ¦(b)  l auquel cas la démonstration s'achève.
Supposons désormais que c < b.
Comme c = sup X, on a :
"x Î ]c, b], x Ï X, c'est-à-dire ¦(x) > l
Soit (yn) une suite d'éléments de ]c, b] qui converge vers c. On a donc :
¦(yn) > l
Or, ¦ est continue en c, donc par passage à la limite :
¦(c)  l
Bilan : on a donc ¦(c) = l, ce qui achève la démonstration.
Autre démonstration à l'aide du théorème des segments emboîtés :
Supposons ¦(a) < ¦(b). (Quitte à poser g = -¦ sinon)
Soit u le milieu de [a, b].
Notons a1 = a et b1 = u si ¦(u)  l.
Notons a1 = u et b1 = b si ¦(u) < l.
Ainsi, on a toujours : ¦(a1)  l  ¦(b1)
En réitérant ce procédé, on construit, par récurrence, une suite de segments emboîtés :
[a, b] É [a1, b1] É ... É [an, bn] É ...
De plus, par construction, la longueur de [an, bn] est
b-a
.
2n
Les segments [an, bn] ont donc des longueurs qui tendent vers 0. Les suites (an) et (bn) sont donc adjacentes.
Notons c leur limite commune. Montrons que ¦(c) = l.
On a, pour tout n Î * :
Par passage à la limite :
Or, ¦ est continue, donc :
¦(an)  l  ¦(bn)
lim ¦(an)  l  lim ¦(bn)
n ® +¥
n ® +¥
¦(c)  l  ¦(c)
Donc ¦(c) = l.
Page 4
Attention : le théorème ne s'applique pas si a et b Î I (dans le cas où I n'est pas fermé). Considérer, par
exemple, la fonction "partie entière" E qui est continue sur [0, 1[. On a E(0) = 0 et E(1) = 1. Mais il n'existe pas
de réel c tel que E(c) =
1
...
2
Application : toute fonction polynomiale (à coefficients réels) de degré impair admet une racine réelle.
1.5. Corollaire
Soit ¦ une application continue sur un intervalle I et à valeurs dans .
Alors ¦(I) est un intervalle.
Démonstration : on utilise ici le fait que les intervalles de  sont les convexes de .
Soient y1 et y2 dans ¦(I) avec y1  y2. Il s'agit de montrer tout élément l de [y1, y2] est élément de ¦(I).
Comme y1 et y2 sont dans ¦(I), il existe a et b dans I tels que ¦(a) = y1 et ¦(b) = y2.
Comme I est un intervalle, on a [a, b] Ì I.
Comme ¦ est continue sur [a, b] (puisque [a, b] Ì I), on a, d'après le théorème des valeurs intermédiaires :
"l Î [y1, y2], $c Î [a, b] tel que ¦(c) = l.
l Î ¦(I)
D'où :
Donc ¦(I) est bien un intervalle.
2. Continuité uniforme
2.1. Définition
Soit ¦ une fonction définie sur un intervalle I.
On dit que ¦ est uniformément continue (ou ¦ est u-continue) sur I lorsque :
"e Î  *+ , $h Î  *+ , "(x, y) Î I 2 : (|x - y|  h Þ |¦(x) - ¦(y)|  e)
La notion de continuité uniforme est globale (h ne dépend que e)
Il est clair que la continuité uniforme sur I entraîne la continuité sur I.
Par contre, la réciproque est fausse : l'application x a x 2 n'est pas uniformément continue sur . (Voir
annexe)
Exercice : comportement d'une fonction uniformément continue au voisinage d'un point
Soit ¦ une fonction u-continue sur un intervalle I du type ]a, b[ (b étant fini ou non)
1. Soit (xn) une suite d'éléments de I qui converge vers a. Alors la suite (¦(xn)) converge.
2. En déduire que ¦ admet une limite finie à droite en a.
Solution :
1. Fixons e Î  *+ . Comme ¦ est uniformément continue sur I, on a :
$h Î  *+ , "(p, q) Î 2, (|xp - xq|  h Þ |¦(xp) - ¦(xq)|  e)
Mais puisque (xn) converge, elle est de Cauchy. Donc :
$N Î , "(p, q) Î 2, (p > q  N Þ |xp - xq|  h)
Page 5
On a alors par transitivité des implications :
$N Î , "(p, q) Î 2, (p > q  N Þ |¦(xp) - ¦(xq)|  e)
Ce qui montre que la suite (¦(xn)) est de Cauchy dans  complet donc converge vers un certain réel l.
2. Fixons e Î  *+ . Comme ¦ est uniformément continue sur I, on a :
$h Î  *+ , "x Î I, "n Î , (|x - xn|  h Þ |¦(x) - ¦(xn)|  e)
Comme la suite (xn) converge vers a :
$N0 Î , "n Î , (n  N0 Þ |xn - a| 
h
)
2
Comme la suite (¦(xn)) converge vers l :
$N1 Î , "n Î , (n  N1 Þ |¦(xn) - l|  e)
Pour n  N0 , on a alors :
0 < |x - a| 
h
h
h
Þ |x - xn|  |x - a| + |a - xn| 
+
h
2
2
2
h
. Ainsi, pour n  max{N0, N1}, on a :
2
h
Þ |x - xn|  h Þ |¦(x) - l|  |¦(x) - ¦(xn)| + |¦(xn) - l|  2e
0 < |x - a| 
2
Ce qui prouve que ¦(x) tend vers l lorsque x tend vers a par valeurs supérieures.
Posons h' =
Un des intérêts de cet exercice réside dans la contraposée de la question 2 :
Si ¦ est définie sur I = ]a, b[ (b Î ¡ ) et n'admet pas de limite finie en a, alors ¦ n'est pas u-continue sur I.
Ainsi, des fonctions telles que x a
1
1
, x a ln x et x a sin
ne sont pas uniformément continues sur  *+ .
x
x
Le théorème suivant donne une condition suffisante pour qu'une fonction soit uniformément continue :
2.2. Théorème Application lipschitzienne
Soit ¦ une fonction lipschitzienne sur un intervalle I ($k Î +, "(x, y) Î I2 : |¦(x) - ¦(y)|  k|x - y|).
Alors ¦ est uniformément continue sur I.
Démonstration
Soit ¦ une fonction lipschitzienne sur I.
Soit e Î  *+ . Posons h =
e
. Soient x et y dans I tels que |x - y|  h. On a alors :
k
|¦(x) - ¦(y)|  k|x - y|  e
Ceci prouve que ¦ est uniformément continue sur I.
Exemple : ¦ : x a
x
. La fonction ¦ est impaire et pour tout (x, y) Î +, on a :
1+ x
|¦(y) - ¦(x)| =
y
x
| y-x|
=
 |y - x|
1+ y 1+ x
(1 + x)(1 + y )
Donc ¦ est 1-lipschitzienne sur + donc elle l'est aussi sur  (puisque ¦ impaire).
On donnera d'autres exemples en annexe.
Page 6
Remarques :
· la réciproque du théorème 2.2. est fausse. L'application x a
x est uniformément continue sur + mais
non lipschitzienne. (Voir annexe)
· par contraposition, on a :
¦ non u-continue sur I Þ ¦ non lipschitzienne sur I
Exercice : Comportement global d'une fonction uniformément continue.
Soit ¦ : + ®  une application uniformément continue.
Alors, il existe des réels a et b tels que :
"x Î +, ¦(x)  ax + b
Preuve :
Fixons e = 1.
Par hypothèse :
$h Î  *+ , "(x, y) Î ¡ 2+ , |x - y|  h Þ |¦(x) - ¦(y)|  1
Soit x Î +.
Idée : on subdivise l'intervalle
x
h
n
Soit n un entier naturel non nul tel que :
[0, x] en n tranches de largeurs
æxö
Remarque : cet entier n existe toujours, il suffit de choisir par exemple n = E ç ÷ + 1.
è hø
inférieures à h.
Pour tout k Î 0, n - 1, l'hypothèse d'uniforme continuité nous permet d'écrire :
¦ æç
è
(k + 1) x ö
æ kx ö
÷ - ¦ç ÷  1
n ø
è nø
En sommant ces inégalités pour k allant de 0 à n - 1, nous obtenons :
n -1
å ¦ æçè
k =0
(k + 1) x ö
æ kx ö
÷ - ¦ç ÷  n
n ø
è nø
Mais d'après l'inégalité triangulaire :
|¦(x) - ¦(0)| 
n -1
å ¦ æçè
k =0
(k + 1) x ö
æ kx ö
÷ - ¦ç ÷
n ø
è nø
On a donc :
x
æxö
|¦(x) - ¦(0)|  n  E ç ÷ + 1 
+2
h
è hø
¦(x) 
En particulier :
Il suffit de poser a =
x
+ 2 + ¦(0)
h
1
et b = 2 + ¦(0) pour achever la démonstration.
h
Remarque : on peut rechercher des majorations affines plus précises en choisissant un e plus petit.
Application : par contraposition, on a :
Si ¦ : + ®  n'est pas majorée par une fonction affine sur +, alors elle n'est pas u-continue sur +.
Par exemple, les fonctions polynômes de degré supérieur ou égal à 2 ne sont pas u-continues sur +.
Page 7
Remarque : on a un résultat analogue sur -. Mais pas d'extension possible à  tout entier. En effet la fonction
valeurs absolue est uniformément continue sur  (puisque 1-lipschitzienne) et pourtant elle n'est majorée par
aucune fonction affine sur .
2.3. CNS pour qu'une fonction dérivable soit lipschitzienne :
Soit ¦ dérivable sur un intervalle I. Alors :
¦ est lipschitzienne sur I Û ¦' est bornée sur I
Démonstration :
Þ Supposons ¦ lipschitzienne sur I : $k Î +, "(x, y) Î I2 : |¦(x) - ¦(y)|  k|x - y|
-k 
Soit x Î I. Comme : "y Î I
¦( y ) - ¦ ( x )
k
y-x
On déduit, par passage à la limite lorsque y tend vers x :
k  ¦'(x)  k
Ceci, quelque soit x Î I. Donc ¦' est bornée sur I.
$M Î  *+ , "t Î I, |¦'(t)|  M.
Ü Supposons ¦' bornée :
Soit (x, y) Î I2. D'après l'inégalité des accroissements finis appliquée à ¦ sur le segment [x, y] :
|¦(y) - ¦(x)|  M|x - y|
Donc ¦ est M-lipschitzienne.
Évidemment, par contraposition, on a pour ¦ dérivable sur I :
¦ est non lipschitzienne sur I Û ¦' n'est pas bornée sur I
Exemple : x a argch x est non lipschitzienne sur ]1, +¥[.
En effet, pour x > 1, argch' x =
1
x -1
2
qui n'est pas bornée sur ]1, +¥[.
2.4. Théorème de Heine
Toute fonction numérique continue sur un segment I est uniformément continue sur ce segment I.
On rappelle qu'un segment est un intervalle fermé borné.
Démonstration :
Soit ¦ une fonction continue sur I.
Supposons ¦ non uniformément continue sur I.
Alors : $e Î  *+ tel que :
"h Î  *+ , $(x ; y) Î I2 tel que : (|x - y|  h et |¦(x) -¦(y)| > e)
En particulier, en choisissant h =
1
(n Î *),
n
Page 8
1
et |¦(xn) -¦(yn)| > e)
n
"n Î *, $(xn ; yn) Î I2 tel que : (|xn - yn| 
(1)
Comme I est borné, les suites (xn) et (yn) ainsi définies le sont également.
D'après le théorème de Bolzano-Weierstrass, on peut donc en extraire des sous-suites qui convergent.
Soit s : * ® * une application strictement croissante telle que la suite ( xs ( n ) ) converge.
Notons l sa limite. (On a nécessairement l Î I puisque I est fermé).
Fixons e' Î  *+ . On a donc :
$N1 Î , "n Î , (n  N1 Þ |xs(n) - l| 
e¢
)
2
Mais, d'autre part, pour tout n Î*, on a d'après (1) :
| xs ( n ) - ys ( n ) | 
Comme
1
s (n )
1
tend vers 0, on a :
s (n )
$N2 Î , "n Î , (n  N2 Þ
1
e¢
 )
s(n)
2
Pour tout n  max(N1, N2) , on a alors :
|ys(n) - l|  |ys(n) - xs(n)| + |xs(n) - l| 
e¢
e¢
+
 e'
2
2
Ceci prouve que la suite ( ys( n ) ) converge également vers l.
Or, ¦ étant continue sur I, on peut affirmer (d'après le théorème 1.2) que les suites
( ¦ ( xs( n) ) )
et ( ¦ ( ys ( n ) ) )
convergent vers ¦(l). Donc :
$N Î , "n Î , (n  N Þ ¦( ys ( n ) ) - ¦ ( xs( n ) )  e)
Ce qui contredit (1).
Conclusion : ¦ est uniformément continue sur le segment I.
Exercice :
Soient a un réel et ¦ une application continue sur [a, +¥[ admettant une limite finie en +¥.
Alors ¦ est uniformément continue sur [a, +¥[.
Solution :
Soit e Î  *+ .
Notons l la limite de ¦ en +¥. On a donc, par hypothèse :
$A Î  *+ , "x Î [a, +¥[, (x  A Þ |¦(x) - l|  e)
Par ailleurs, d'après le théorème de Heine, ¦ est uniformément continue sur le segment [a, A] :
$h Î  *+ , "(x, y) Î [a, A]2, (|x - y|  h Þ |¦(x) - ¦(y)|  e)
Page 9
Montrons que ¦ est uniformément continue sur [a, +¥[.
Soit (x, y) Î [a, +¥[2. Supposons x  y (ce n'est pas une perte de généralité) et |x - y|  h (pour le h ci-dessus)
Distinguons trois cas :
xyA
Dans ce cas, comme ¦ est uniformément continue sur [a, A], il vient :
|¦(x) - ¦(y)|  e  2e
Axy
Dans ce cas, comme ¦ admet une limite finie l en +¥, on a par l'inégalité triangulaire
|¦(x) - ¦(y)|  |¦(x) - l| + |¦(y) - l|  2e
xAy
Alors |x - A|  |x - y|  h
Coupons en ¦(A) :
|¦(x) - ¦(y)|  |¦(x) - ¦(A)| + |¦(y) - ¦(A)|  2e
Bilan : on a prouvé :
"e Î  *+ , $h Î  *+ , "(x, y) Î [a, +¥[2, (|x - y|  h Þ |¦(x) - ¦(y)|  2e)
D'où l'uniforme continuité de ¦ sur [a, +¥[.
3. Applications
3.1. Théorème Fonction continue sur un segment
Soit I = [a, b] un segment de  et ¦ : I ®  une application continue.
Alors ¦ est bornée sur I et ¦ atteint ses bornes.
C'est une application du théorème des segments emboîtés et du théorème de Bolzano-Weierstrass.
Démonstration :
1. Montrons : ¦ bornée sur I
Supposons ¦ non bornée sur I.
Soit c le milieu de I.
Posons a1 = a et b1 = c si ¦ non bornée sur [a, c].
Posons a1 = c et b1 = b sinon.
En réitérant ce procédé, on construit, par récurrence, une suite de segments emboîtés :
[a, b] É [a1, b1] É ... É [an, bn] É ...
Sur chacun de ces intervalles, ¦ est, par construction, non bornée.
De plus, par construction, la longueur de [an, bn] est
b-a
.
2n
Les segments [an, bn] ont donc des longueurs qui tendent vers 0. Les suites (an) et (bn) sont donc adjacentes.
Notons x0 leur limite commune.
Page 10
Comme ¦ est continue en x0, on a (avec e = 1) :
$h Î  *+ , "x Î I : (|x - x0|  h Þ |¦(x) - ¦(x0)|  1)
C'est-à-dire :
$h Î  *+ , "x Î I : (|x - x0|  h Þ ¦(x0) - 1  ¦(x)  ¦(x0) + 1)
Donc ¦ est bornée sur ]x0 - h, x0 + h[.
Comme les segments [an, bn] ont des longueurs qui tendent vers 0, on a :
"e Î  *+ , $N Î * : (n  N Þ bn - an  e)
Donc, pour un certain N, les segments [an, bn], n  N, sont contenus dans ]x0 - h, x0 + h[.
Or, ¦ n'est pas bornée sur [an, bn] d'où une contradiction.
Donc ¦ est bornée sur I.
2. Montrons : ¦ atteint ses bornes
On vient de voir que ¦ est bornée sur I. Notons M = sup ¦ et m = inf ¦.
I
I
Montrons qu'il existe x0 dans I tel que ¦(x0) = M.
Comme M est la borne supérieure de ¦ sur I :
"e Î  *+ , $x Î I : M - e < ¦(x)  M
En particulier, avec e =
1
:
n
$xn Î I : M -
1
< ¦(xn)  M
n
La suite (¦(xn)) converge donc vers M.
En outre, la suite (xn) est bornée. D'après le théorème de Bolzano-Weierstrass, on peut donc en extraire une
sous suite qui converge vers un certain réel x0. Notons s : * ® * une application strictement croissante telle
que ( xs ( n ) ) converge vers x0.
La fonction ¦ étant continue en x0, on a : M = lim ¦ ( xs ( n ) ) = ¦(x0).
n ® +¥
Donc ¦ atteint son maximum.
On démontre, de même, que ¦ atteint son minimum.
3.2. Théorème Point fixe
On peut remplacer l'hypothèse "¦ : I
Soit I un intervalle fermé non vide.
par "¦ : I
Soit ¦ : I ® I une application contractante sur I.
®
I contractante"
®  contractante et telle que ¦(I) Ì I "
On rappelle que "¦ contractante sur I " signifie :
Alors :
$k Î [0, 1[, "(x, y) Î I2, |¦(y) - ¦(x)|  k|y - x|
1) ¦ admet un unique point fixe l dans I.
u ÎI
converge vers l.
2) "u0 Î I, la suite u :  ®  définie par ìí 0
î"n Î ¥, un +1 = ¦ (un )
Démonstration
Remarquons au préalable que, u0 étant dans I et I étant stable par ¦, la suite (un) est bien définie et :
"n Î , un Î I
Page 11
Existence d'un point fixe :
Montrons, par récurrence sur n Î , la propriété :
Ã(n) : |un+1 - un|  kn|u1 - u0|
· On a évidemment Ã(0).
· Montrons que pour tout n Î , Ã(n) Þ Ã(n + 1) :
Soit n Î . Supposons Ã(n). Alors :
|un+2 - un+1| = |¦(un+1) - ¦(un)|
¦ contractante

¦(I ) Ì I
Ã( n )
k|un+1 - un|  kn+1|u1 - u0|
D'où Ã(n + 1).
Du principe de raisonnement par récurrence, on déduit :
"n Î , Ã(n) : |un+1 - un|  kn|u1 - u0|
Déduisons-en que (un) est de Cauchy :
Soit e Î  *+ .
Soit (p, q) Î 2 avec q > p  0.
Notons r = q - p.
On a :
p + r -1
å
|uq - up| = |up+r - up| =
p + r -1
ui +1 - ui 
i= p
å
p + r -1
| ui +1 - ui | 
i= p
å
i
| u1 - u0 |
i= p
p + r -1
Or :
åk
k i | u1 - u0 | = kp |u1 - u0|
i= p
r -1
åk
i
i =0
Et comme k Î [0, 1[, la série géométrique de terme général ki converge et est majorée par
|uq - up| 
D'où :
kp
1- k
Et enfin, toujours parce que k Î [0, 1[ :
1
.
1- k
kp
|u1 - u0|
1- k
¾¾¾¾
®
p ®¥
0
En conséquence :
$N Î , "p Î , (p  N Þ
kp
|u1 - u0|  e Þ |uq - up|  e)
1- k
Ce qui prouve que la suite (un) est de Cauchy.
Et comme  est complet, (un) converge.
Notons l sa limite. Comme I est fermé, on a l Î I.
Or, ¦ est continue en l (puisque contractante sur I) donc, d’après le théorème 1.2. :
l = ¦(l)
On a donc prouvé que ¦ admet un point fixe l dans I et que (un) converge vers l.
Unicité du point fixe :
Supposons :
$l, l' Î I, ¦(l) = l et ¦(l') = l'
Page 12
Comme ¦ est contractante sur I :
|¦(l) - ¦(l')|  k|l - l'|
|l - l'|  k|l - l'|
(1 - k)|l - l'|  0
|l - l'|  0
Or, k Î [0, 1[, donc :
l = l'
Remarques :
· L'hypothèse "I fermé" n'est là que pour assurer l Î I. Si on sait déjà, par ailleurs, que l Î I (en pratique, on
a parfois déjà calculé l en résolvant l'équation ¦(l) = l), cette hypothèse devient inutile.
· Le théorème du point fixe ne s'applique pas si l'on remplace l'hypothèse "¦ contractante sur I " par
l'hypothèse "¦ 1-lipschitzienne sur I ". Voici un contre-exemple :
¦:I ® I
I = [1, +¥[
x a x+
1
x
Soient x et y dans I avec x < y.
Comme ¦ est croissante sur [1, +¥[, on a :
|¦(y) - ¦(x)|  ¦(y) - ¦(x)  y - x +
x- y
 y - x  |y - x|
xy
Ce qui prouve que ¦ est 1-lipschitzienne sur I.
Cependant ¦ n'a pas de point fixe sur I. (L'équation ¦(x) = x n'a pas de solution)
y
D
Exemple :
C¦
Étudier la convergence de la suite définie par :
ìu0 Î [-1, +¥[
í
îun +1 = 1 + un
1
On introduit l’application ¦ définie sur [-1, +¥[ par :
"x Î , ¦(x) = 1 + x
O
u0
1
f
Point fixe de ¦ :
¦(x) = x Û
1 + x = x Û x  0 et x 2 - x - 1 = 0 Û x = f =
1+ 5
2
On montre facilement que ¦ est dérivable sur ]-1, +¥[, croissante sur [-1, +¥[, puis que :
¦([-1, +¥[) = [0, +¥[ Ì [-1, +¥[
L’intervalle I = [-1, +¥[ est donc stable et la suite (un) est bien définie.
Page 13
x
"x Î +, |¦’(x)| =
De plus :
1
1

2
2 1+ x
D’après l’inégalité des accroissements finis :
"(a, b) Î + ´ +, |¦(b) - ¦(a)| 
Donc ¦ est
1
1
|b - a|
2
-lipschitzienne sur I, donc contractante sur I.
2
¦(+) = [1, +¥[ Ì +
En outre :
Donc + est stable par ¦.
ìu0 Î ¡ +
D’après le théorème du point fixe, la suite (un) définie par í
converge donc vers f.
îun +1 = 1 + un
Enfin, si u0 Î [-1, 0] alors u1 Î + et d’après ce qui précède, (un) converge encore vers f.
3.3. Sommes de Riemann
Contexte :
· ¦ est une application continue définie sur un segment [a, b] et à valeurs dans .
· s = (ai )0i n est une subdivision de [a, b]. (Cela signifie : a = a0 < a1 < ... < an = b)
· h est le pas de la subdivision s. (C'est-à-dire : h = max(ai +1 - ai ) )
i
· "i Î 0, n - 1, xi Î [ai , ai + 1].
On appelle alors somme de Riemann associée à (¦, s, (xi ) 0i n) le réel :
n -1
å (a
i +1
- ai ) ¦ (x i )
i =0
Théorème
n -1
lim
h ®0
å (a
i +1
- ai ) ¦ (x i ) =
i =0
ò
b
¦ ( x) dx
a
Démonstration :
Montrons que la différence suivante peut être rendue aussi petite que voulue :
ò
b
¦ ( x) dx -
a
n -1
å
(ai +1 - ai ) ¦ (x i ) =
i =0
n -1
æ
ç
i =0 è
åò
ai +1
ai
ö
¦ ( x ) dx - (ai +1 - ai ) ¦ (x i ) ÷ =
ø
n -1
æ
å çè ò
i =0
ai +1
ai
(¦( x) - ¦(xi ) )dx ö÷
ø
En passant aux valeurs absolues, on a la majoration suivante :
ò
b
¦ ( x) dx -
a
n -1
å
(ai +1 - ai ) ¦(xi ) 
i =0
n -1
æ
å çè ò
i =0
ai +1
ai
ö
¦ ( x ) - ¦ (x i ) dx ÷
ø
Or, du théorème de Heine appliqué à ¦ continue sur le segment [a, b], on déduit :
¦ uniformément continue sur [a, b] (et donc aussi sur chaque [ai , ai+1])
C'est-à-dire :
"e Î  *+ , $h Î  *+ , "(x, y) Î [a, b]2 : (|x - y| < h Þ |¦(x) - ¦(y)| < e)
Pour une subdivision s de pas h tel que : 0 < h < h, on aura :
Page 14
"x Î [ai+1, ai ], |x - xi |  ai+1 - ai  h < h
|¦(x) - ¦(xi )| < e
Ce qui entraînera :
Dans ces conditions, on peut écrire :
ò
b
¦ ( x) dx -
a
n -1
å
( ai + 1 - ai ) ¦ ( x i ) 
i =0
n -1
Ceci prouve bien que :
å (a
lim
i +1
h ®0
n -1
æ
ç
i =0 è
åò
ai +1
ai
n -1
ö
e dx ÷ =
e(ai +1 - ai ) = e(b - a)
ø i =0
å
ò
- ai ) ¦ (x i ) =
i =0
b
¦ ( x) dx
a
Toute intégrale d'une fonction continue sur un segment est donc une limite de somme de Riemann.
Remarque : le résultat ci-dessus reste valable si ¦ est continue par morceaux. Il suffit de refaire la même
démonstration avec des subdivisions adaptées à ¦.
Cas particulier d'une subdivision régulière :
Pour n Î *, on particularise : ai = a + i
b-a
b-a
et xi = ai . (Donc h =
)
n
n
ai+1 - ai =
On a alors :
D'où :
lim
n ® +¥
b-a
n
n -1
å ¦æçè a + i
i =0
b-a
n
b-aö
÷=
n ø
ò
b
¦ ( x) dx
a
Cas particulier des fonctions définies sur [0, 1] :
La formule ci-dessus devient alors :
lim
n ® +¥
Remarque : en particularisant : ai = a + i
On a alors :
lim
n ® +¥
n ® +¥
n -1
å ¦æçè n ö÷ø = ò
i
i =0
b
¦ ( x) dx
a
b-a
et xi = ai+1
n
b-a
n
lim
1
n
n -1
å ¦æçè a + (i + 1)
i =0
n
b-a
n
å ¦æçè a + i
lim
1
n
i =1
b-aö
÷=
n ø
b-aö
÷=
n ø
ò
ò
b
b
¦ ( x) dx
a
¦ ( x) dx
a
D'où aussi :
n ® +¥
n
å ¦æçè n ö÷ø = ò
i
i =1
b
¦ ( x) dx
a
Exemples :
n
1. Étudier la limite de la somme :
å n+i .
1
i =1
Page 15
1
.
1+ x
On considère l'application ¦ définie sur [0, 1] par ¦(x) =
On a alors :
lim
n ® +¥
n
å
1
n
1
i
i =1 1 +
n
n
lim
n ® +¥
1
ò 1 + x dx
=
å n + i = ln 2
1
i =1
2. Étudier la limite de la suite (un) définie par : un = n
n -1
å (n + i )
1
i =0
On considère l'application ¦ définie sur [0 ; 1] par ¦(x) =
On a alors :
lim
n ® +¥
1
n
n -1
åæ
i =0
1
iö
ç1 + ÷
n
è
ø
2
=
n -1
lim n
n ® +¥
1
0
1
.
(1 + x) 2
ò
1
0
å (n + i )
1
i =0
2
2
1
dx
(1 + x) 2
=
1
2
1
æ (2n)! ö n
lim ç
÷
n ® +¥ è n! n n ø
3. Déterminer la limite suivante :
Pour tout n Î *, on a :
1
2n
n
n
ö 1 æ 2n
ö 1 æ 2n
k ö÷ 1 æç
k + n ö÷
æ (2n)! ö n 1 æç
÷= ç
÷= ç
ln ç
=
ln
k
ln
k
n
ln
n
ln
k
n
ln
n
ln
=
ln
÷
n
÷ n ç
÷ n ç
÷
ç
n çè k =1
n ÷ø
è n!n ø
k =1
ø
è k = n +1
ø
è k = n +1 n ø n è k =1
å
å
å
1
å
å
n
(2n)! ö n 1 æç
æ k ö ö÷
ln
ln æç
=
ç1 + ÷
÷
n çè k =1 è n ø ÷ø
è n!nn ø
D'où
å
On considère maintenant l'application ¦ définie sur [0, 1] par ¦(x) = ln(1 + x)
On a alors : lim
n ® +¥
1
n
n
å lnæçè1 + n ö÷ø = ò ln(1 + x) dx = [(1 + x) ln(1 + x) - (1 + x)]
i =1
i
1
0
1
0=
2 ln 2 - 1 = ln 4 - 1
1
D'où :
æ (2n)! ö n = 4
lim ç
÷
n ® +¥ è n ! n n ø
e
Page 16
3.4. Approximation d'une fonction continue sur un segment par des fonctions en escalier
Théorème
Soit ¦ une application continue sur un segment [a, b].
Soit e Î +.
Il existe des applications en escaliers j et y telles que :
j  ¦  y sur [a, b] et y - j  e sur [a, b]
Démonstration
Pour tout n Î *, on définit une subdivision régulière {a0, a1, ..., an} du segment [a, b] par :
"k Î 0, n, ak = a + k
b-a
n
Comme ¦ est continue sur [a, b], elle l'est aussi sur chacun des segments [ak, ak+1] (0  k  n - 1), donc y est
bornée, ce qui permet de définir :
Mk =
sup
t Î[ ak , ak +1 ]
¦ (t )
et
mk =
inf
t Î[ ak , ak +1 ]
¦ (t )
On définit alors des applications en escalier j et y sur [a, b] par :
"k Î 0, n - 1, "t Î [ak, ak+1[, j(t) = mk et y(t) = Mk
j(b) = mn-1 et y(b) = Mn-1
et :
j  ¦  y sur [a, b]
Ainsi, on a bien :
Par ailleurs, ¦ étant continue sur le segment [a, b], elle y est uniformément continue (théorème de Heine) :
"e Î  *+ , $h Î  *+ , "(x, y) Î [a, b]2, (|x - y|  h Þ |¦(x) - ¦(y)|  e)
Soit h le réel obtenu pour le réel e fixé dans les hypothèses.
On sait que le pas de la subdivision est :
Soit k Î 0, n - 1 et (x, y) Î [ak, ak+1]. On a donc :
b-a
n
|x - y|  ak+1 - ak 
b-a
n
Choisissons un pas plus fin que h, obtenu pour les entiers n qui vérifient :
æb-aö
n  Eç
÷+1
è h ø
|x - y|  h
Ainsi :
De la continuité uniforme de ¦, on déduit alors :
|¦(x) - ¦(y)|  e
Cette dernière inégalité étant valable pour tous x et y de [ak, ak+1].
En particulier pour un x tel que ¦(x) = Mk et un y tel que ¦(y) = mk (existent bien car ¦ atteint ses bornes) :
Mk - mk  e
D'où
y - j  e sur chaque [ak, ak+1] et donc sur [a, b]
Remarque : cette démonstration peut être adaptée aux fonctions continues par morceaux sur le segment [a, b].
Page 17
4. Annexe : étude de quelques fonctions usuelles
On a vu que :
¦ lipschitzienne Þ ¦ uniformément continue Þ ¦ continue
Par contraposition :
¦ non continue Þ ¦ non uniformément continue Þ ¦ non lipschtienne
Fonction ¦
¦ continue ?
x a x 2 sur 
oui
x a
x sur +
oui
x a ln x sur  *+
oui
1
sur  *+
x
oui
x
sur 
1+ x
oui
1
sur *
x
oui
x a
xa
x a sin
x a sin x sur 
¦ uniformément continue ?
¦ lipschitzienne ?
non
non
(voir démonstration ci-dessous)
oui
non
non
non
(voir démonstration en exercice section 2.1.)
non
non
oui
oui
(voir démonstration en section 2.2.)
non
non
oui
oui
oui
Quelques preuves
Non continuité uniforme de x a x 2 sur 
1
h
et y = x + :
h
2
Prenons e = 1. Pour tout h Î  *+ , on a en choisissant un réel x >
y-x=
h2
h
> xh > 1
et y 2 - x 2  xh +
4
2
|y - x|  h et y 2 - x 2 > e
C'est-à-dire :
On a bien prouvé :
$e Î  *+ , "h Î  *+ , $(x, y) Î 2, (|x - y|  h et | x 2 - y 2 | > e)
Donc la fonction x a x 2 n'est pas uniformément continue sur .
Uniforme continuité de x a
x sur +
Une inégalité bien pratique :
Pour tout (x, y) Î + avec x  y, on a :
y-
x  y-x
Preuve :
(
Par croissance de t a
x+ y-x
)
2
= y + 2 x( y - x  y  0
t sur +, il vient :
x+
y-x 
y
D'où le résultat.
Page 18
Soit e Î  *+ . Pour h < e2, on a :
Soit (x, y) Î + tel que |x - y|  h. Alors
| y- x |
D'où la continuité uniforme de x a
x a
y-x e
x sur +.
x n'est pas lipschitzienne sur +
Si elle l'était, il existerait un réel K Î + tel que pour tout (x, y) Î + ´ +, on ait :
| y - x |  K |y - x|
Si K = 0, cela entraînerait
y = x pour tout (x, y) Î + ´ +, ce qui est absurde.
Si K Î  *+ , il suffit de choisir x = 0 et y =
1
pour avoir une contradiction.
4K 2
Page 19

Fonctions continues et uniformement continues

Transcription

Documents pareils

Feuille d`exercices 2 Fonctions : continuité-dérivation

I) Auto-test : Continuité

CONCOURS NATIONAL MAROCAIN - Session 2016

Le théorème de Cauchy-Péano par la méthode d`Euler explicite

Comment organiser son travail et bien travailler les maths en prépa ?

3ème Activité – Théorème de Thalès 2011/2012

3ème Révisions brevet blanc de mathématiques

Intégration TD1 Intégrale de Lebesgue : théorèmes de convergence

Test 3 EXERCICE 1 : (2 points) f est de la forme u × v3 où u : x ↦→ x

Première S2. Corrigé du DS de Mathématiques du janvier-2010