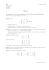Série d`exercices: Matrice

Série d’exercices: Matrice
Exercice 1 Effectuer le produit des matrices :


−1 −1 0
1 −1
1 2 0
2 1
4 −1 
×
× 1
3 2
1 1
3 1 4
2
1
2
Exercice 2 On considère la matrice suivante

0
 0
M =
 0
0

 

a b c
1 a c
 c b a × 1 b b 
1 1 1
1 c a
:
a
0
0
0
b
d
0
0

c
e 

f 
0
Calculer M 2 , M 3 , M 4 , M 5 .
Exercice 3 On considère les trois matrices suivantes :




7 2
2 −3 1 0
 −5 2 


5 4
1 3 
A=
B=
 3 1 
6 −2 −1 7
6 0
et C =
−1 2 6
3 5 7
1. Calculer AB puis (AB)C.
2. Calculer BC puid A(BC).
3. Que remarque-t-on ?
Exercice 4 On considère les

2
 5
A=
 3
2
deux matrices suivantes :


3 −4 1

2 1 0 
,
B=


1 −6 7
4 0 1

3 −1 −3 7
4 0
2
1 

2 3
0 −5 
1 6
6
1
1. Calculer AB.
2. Calculer BA.
3. Que remarque-t-on ?


1 0 0
Exercice 5 Trouver les matrices qui commutent avec A =  0 1 1  . De même avec A =
3 1 2
a b
.
0 a
1


0 1 1
Exercice 6 Soit A =  1 0 1  . Calculer A2 et vérifier que A2 = A + 2I3 , où I3 est la
1 1 0
matrice identité 3 × 3. En déduire que A est inversible et calculer son inverse.


1 1 0
Exercice 7
1. Soit A =  0 1 1  et soit B = A − I3 .
0 0 1
(a) Calculer B 2 , B 3 en déduire une formule de récurrence que l’on démontrera pour B n ,
pour tout entier n.
(b) Développer (B + I3 )n par la formule du binôme et simplifier.
(c) En déduire An Pour tout entier n.


1 1 1 1
 0 1 1 1 
n

2. Soit A = 
 0 0 1 1  . Pour tout entier n, calculer A en utilisant A − I4 .
0 0 0 1


1 0 0
Exercice 8
1. On considère la matrice A =  0 1 1  .
3 1 1




1 1 1
1 1
1
1 
(a) Soient B =  0 1 0  et C =  1 2
1 0 0
0 −1 −1
Montrer que AB = AC, a-t-on A = C ? A peut-elle être inversible ?
(b) Déterminer toutes les matrices F telles que A × F = O (O étant la matrice dont
tous les coefficients sont nuls).


1 2
2. Soit A =  3 4 . Déterminer toutes les matrices B telles que BA = I2 .
−1 4
3. Soient A et B deux matrices carrées n × n telles que AB = A + In .
Montrer que A est inversible et déterminer son inverse (en fonction de B).
Exercice 9 Soit A une matrice carrée d’ordre n ; on suppose que A2 est une combinaison
linéaire de A et In : A2 = αA + βIn .
1. Montrer que An est également une combinaison linéaire de A et In pour tout n ∈ N∗ .
2. Montrer que si β est non nul, alors A est inversible et que A−1 est encore combinaison
linéaire de A et In .
3. Application 1 : soit A = Jn − In , où Jn est la matrice Attila (envahie par les uns...),
avec n > 1. Montrer que A2 = (n − 2) A + (n − 1) In ; en déduire que A est inversible, et
déterminer son inverse.
4. Application 2 : montrer que si n = 2, A2 est toujours une combinaison linéaire de A et
I2 , et retrouver la formule donnant A−1 en utilisant 2.
2


−1 1
1
Exercice 10 Soit A =  1 −1 1 
1
1 −1
Calculer A2 et montrer que A2 = 2I − A, en déduire que A est inversible et calculer A−1 .


1 0 2
Exercice 11 Soit A = 0 −1 1 . Calculer A3 − A. En déduire que A est inversible puis
1 −2 0
−1
déterminer A .


0 0 0
Exercice 12 Soit A = −2 1 −1.
2 0 2
1. Calculer A3 − 3A2 + 2A.
2. Quel est le reste de la division euclidienne de X n par X 3 − 3X 2 + 2X ?
3. Calculer