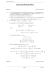Formulaire de Mathématiques

MATHÉMATIQUES
I-
COMPLEXES, EQUATIONS DIFÉRENTIELLES, FONCTIONS USUELLES
Nombres complexes
Dans le repère orthonormal (O; ~u, ~v ) le point
M (x, y), où (x, y) ∈ R2 , a pour affixe z.
y
•
M (z)
Propriétés des modules pour (z, z 0 ) ∈ C2
– z z̄ = |z|2
– |z| = |z̄|
|z |
O
x
~u
– z a pour forme algébrique : z = x + iy
z + z̄
– partie réelle de z : Re(z) = x =
2
z − z̄
– partie imaginaire de z : Im(z) = y =
2i
– le conjugué de z est : z̄ = q
x − iy
– le module de z est : |z| = x2 + y 2
Pour z 6= 0, en notant θ = arg z son argument :
– z a pour forme trigonométrique :
z = |z| (cos θ + i sin θ)
– z a pour forme exponentielle :
z = |z| eiθ
Propriétés des conjugués pour (z, z 0 ) ∈ C2
– z + z0 = z + z0
II-
1
1
– pour z 6= 0, =
z
|z|
0
0
– |zz | = |z| |z |
– |z n | = |z|n
– |z + z 0 | ≤ |z| + |z 0 |
– Si A et B ont pour affixes respectives zA et zB ,
−→
alors le vecteur AB a pour affixe zB − zA , et la
distance AB = |zB − zA |.
arg (z)
~v
– zz 0 = z · z 0
– z n = (z)n
Propriétés des arguments pour (z, z 0 ) ∈ C2
– arg(−z) = arg(z) + π
– arg (z̄) = − arg(z)
0
– arg (zz
) = arg(z) + arg(z 0 )
1
= − arg(z)
– arg
z z
– arg 0 = arg(z) − arg(z 0 )
z
−→ −−→
d−c
– AB, CD colinéaires ⇐⇒
∈R
b−a
−→ −−→
d−c
∈ iR
– AB, CD perpendiculaires ⇐⇒
b−a
Équations du second degré
Soient a, b et c trois nombres réels (a =
6 0) et
2
2
∆ = b − 4ac. L’équation (E) : az + bz + c = 0
admet :
? si ∆ > 0, deux solutions réelles :
√
√
−b + ∆
−b − ∆
z1 =
et z2 =
2a
2a
? si ∆ = 0, une solution réelle :
z0 =
−b
2a
Document sous licence BY-NC-SA 3.0
? si ∆ < 0, deux solutions complexes conjuguées :
√
√
−b + i −∆
−b − i −∆
z1 =
et z2 =
2a
2a
– si ∆ 6= 0, alors az 2 + bz + c = a(z − z1 )(z − z2 )
– si ∆ = 0, alors az 2 + bz + c = a(z − z0 )2
−b
– z1 + z2 =
a
c
– z1 z2 =
a
Si on résout l’équation (E) dans R, elle admet des
solutions (réelles) uniquement si ∆ ≥ 0.
CC
nicolabricot.com
1/2
MATHÉMATIQUES
III-
COMPLEXES, EQUATIONS DIFÉRENTIELLES, FONCTIONS USUELLES
Équations différentielles
Soient a et b deux réels, avec a 6= 0.
– Les solutions dans R de l’équation différentielle
(E0 ) : y 0 = ay sont les fonctions f définies dans R
de la forme : f (x) = keax , avec k ∈ R.
IV-
– Les solutions dans R de l’équation différentielle
(E) : y 0 = ay + b sont les fonctions f définies dans
b
R de la forme : f (x) = keax − , avec k ∈ R.
a
Fonctions usuelles
y
e
ex
•
ln x
•
1
O
1.
Fonction exponentielle
2.
La fonction f , définie et dérivable sur R, vérifiant
pour tout x ∈ R, f 0 (x) = f (x) et f (0) = 1, est appelée la fonction exponentielle.
Elle est notée : exp(x) = ex , pour x ∈ R.
Fonction logarithme
La primitive sur ]0; +∞[, qui s’annule en 1, de la
fonction x 7→ x1 , est appelée la fonction logarithme.
Z x
dt
Elle est notée : ln(x) =
, pour x > 0.
1 t
Pour tous réels x > 0, y > 0 et n ∈ Q,
Pour tous réels x et y,
– e0 = 1 et ex > 0
– ex+y = exx · ey
e
– ex−y = y
e
– (ex )y = exy
– ln (1) = 0 et ln (e1 ) = 1
– ln (xy)! = ln(x) + ln(y)
x
– ln
= ln (x) − ln (y)
y
– ln (xn ) = n ln(x)
Limites et croissances comparées pour n ∈ N∗
lim ex = 0
et
lim ex = +∞
– x→−∞
x→+∞
ex
– lim xn ex = 0
et
lim n = +∞
x→−∞
x→+∞ x
Document sous licence BY-NC-SA 3.0
x
e
1
Limites et croissances comparées pour n ∈ N∗
lim ln x = +∞
– lim+ ln x = −∞ et
x→+∞
x→0
ln x
– lim
=0
x→+∞ xn
CC
nicolabricot.com
et
lim xn ln x = 0
x→0
2/2