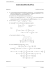Baccalauréat S Amérique du Nord 31 mai 2012 Corrigé de A. Saoud

Baccalauréat S Amérique du Nord 31 mai 2012
Corrigé de A. Saoud Manal
E XERCICE 1
PARTIE A.
5 POINTS
1. Un quart des femmes et un tiers des hommes adhère à la section tennis, donc p F (T) =
et p F (T) =
1
4
1
. 30 % des membres de cette association adhèrent à la section tennis, donc
3
3
.
10
F et F forment une partition, d’après le théorème des probabilités totales, on a : p(T) =
1
3
1
p(T ∩ F) + p(T ∩ F) = p F (T)p(F) + p F (T)p(F) = p(F) + (1 − p(F)) = . On en déduit que
4
3
10
1 3
2
1
p(F) = −
soit p(F) = .
12
3 10
5
2
1
p(T ∩ F) p(F)p F (T) 5 × 4 1
2. Il s’agit de calculer p T (F). Or p T (F) =
=
= 3 = .
p(T)
p(T)
3
10
p(T) =
PARTIE B.
1.
2.
a. C’est une répétition d’une expérience aléatoire à deux issues, identique et indépendante. La variable aléatoire X, donnant le nombre de membres adhérant à la section
tennis parmi les membres choisis, suit donc la loi binomiale de paramètres n = 4
3
. On souhaite deux succès, la probabilité est donc
(nombre d’épreuves) et p =
10¶
à ! µ ¶ µ ¶
à ! µ ¶ µ
2
3 4−2
3 2
7 4−2 1 323
3
4
4
× 1−
=
×
×
=
p(X = 2) =
×
≈ 0, 2646 .
10
10
10
10
5 000
2
2
b. Il suffit de considérer l’évènement
membre
µ ¶ncontraire qui consiste à ne choisir
¶
µ aucun
7
7 n
du club de tennis n fois, soit
. Le résultat est donc p n = 1 −
.
10
10
µ ¶n
µµ ¶n ¶
µ ¶n
7
7
7
> 0, 99,
6 0, 01, ln
6 ln(0, 01) car la fonction ln
c. p n > 0, 99, 1 −
10
10
10
est croissante.
µ ¶
µ ¶
7
ln(0, 01)
7
n ln
6 ln(0, 01), n >
< 0. n > 12, 9, i.e. n > 13.
¡ 7 ¢ car ln
10
10
ln 10
a. Les gains algébriques possibles sont -5, 15, et 35.
Y = yi
15
35
µ
¶
¶
10
10
2
1
89
2
1
p(Y = y i ) µ
=
µ
¶=
¶
¶=
110
11
110
100
100
100
2
2
2
X
¢
¡
2
1
89
+ 15 ×
+ 35 ×
= −1. Le
b. L’espérance est donc E(Y) = y i p Y = y i = −5 ×
110
11
110
i
jeu est en défaveur du joueur car l’espérance est négative ou encore qu’en moyenne,
sur un grand nombre de partie, le joueur perd 1 euro par partie.
µ
90
2
-5
¶
µ
90
1
µ
¶µ
A. P. M. E. P.
Baccalauréat S
E XERCICE 2
PARTIE A. R ESTITUTION
5 POINTS
ORGANISÉE DES CONNAISSANCES
ln(et )
ln(x)
= lim
=
x→+∞ x
t →+∞ et
On pose x = et , on a donc x > 0, ln(x) = t . On a lim et = +∞ = lim x. lim
t →∞
t
et
lim t = 0 puisque lim
= +∞.
t →+∞ e
t →+∞ t
PARTIE B.
t →∞
1
1. La fonction g est dérivable d’après les théorèmes généraux et g ′ (x) = 2x + . Pour x > 1,
x
1
2x > 0 et > 0, donc g ′ (x) > 0 donc la fonction g est strictement croissante sur [1 ; +∞[.
x
v(x)
2.
a. La fonction f (x) = u(x) −
avec u(x) = x et v(x) = ln(x). u et v sont dérivables
u(x)
1
avec u ′ (x) = 1 et v ′ (x) = . D’après les théorèmes généraux f est dérivable et on a
x
1
x 2 − 1 + ln(x) g (x)
v ′ (x)u(x) − v(x)u ′ (x)
x × x − ln(x)
′
′
=
1
−
=
= 2
f (x) = u (x) −
u(x)2
x2
x2
x
2
′
b. Pour tout x ∈ [1 ; +∞[, g (x) > 0 et x > 0, donc f (x) > 0. On en déduit que f est
strictement croissante sur [1 ; +∞[.
ln(x)
ln(x)
c. f (x) − x = −
, lim f (x) − x = − lim
= 0 donc la droite D d’équation
x→+∞
x→+∞ x
x
y = x est une asymptote à la courbe C .
ln(x)
> 0 donc la courbe C est située
d. Pour tout x ∈ [1 ; +∞[, ln(x) > 0 et x > 0, donc
x
en dessous de la droite D.
3.
a. Un graphique pour comprendre :
N5
5
M5
4
C
M3
D
3
M3
2
1
0
Amérique du Nord
1
2
2
3
4
5
31 mai 2012
A. P. M. E. P.
Baccalauréat S
La distance Mk Nk = | f (x) − x| =
Variables
Initialisation
Traitement
Sortie
ln(k)
> 0.
k
k est un entier
d est une variable réelle
ln(k)
k := 2 ; d :=
k
Tant que d > 10−2
Début du tant que
k := k + 1 ;
ln(k)
;
d :=
k
Fin du tant que
Afficher k
E XERCICE 3
5 POINTS
PARTIE A.
b.
1. Pour tout x ∈ [0 ; 1],
sante sur [0 ; 1]
1
> 0, donc f ′ (x) > 0. On en déduit que f est strictement crois1 + x2
2.
a. g est la composée des fonctions f et u : x 7−→ tan(x) qui sont dérivables, donc g est
¡
¢
1
dérivable et g ′ (x) = f ′ (u(x)) × u ′ (x) =
× 1 + tan2 (x) = 1
2
1 + tan (x)
h πi
h πi
b. Pour tout x de 0 ;
, g ′ (x) = 1, donc pour tout x de 0 ;
, g (x) = x + c avec c ∈ R
4
4
une constante. D’autre part, 0 + c = g (0)h = f (tan(0))
= f (0) =³ 0. On en
déduit que
πi ³π´ π
π ´
c = 0. On a donc g (x) = x pour tout x de 0 ;
.g
= = f tan( ) = f (1), donc
4
4
4
4
π
f (1) = .
4
π
π
3. f est croissante sur [0 ; 1]. f (0) = 0 et f (1) = donc, pour tout x ∈ [0 ; 1], 0 6 f (x) 6
4
4
PARTIE B.
1
1. On pose u(x) = x. u et f sont dérivables et leurs dérivées u ′ (x) = 1 et f ′ (x) =
1 + x2
Z1
f (x)d x =
sont continues, d’après le théorème de l’intégration par parties on a I0 =
0
Z1
Z1
Z1
Z
£
¤1
£
¤1
x
1 1 2x
′
′
u (x) f (x)d x = u(x) f (x) 0 − u(x) f (x)d x = x f (x) 0 −
d x = f (1)−
d x.
2
2 0 1 + x2
0 1+x
0
0
2
′
On pose pour tout x de [0 ; 1], v(x) = 1+x . v est dérivable avec v (x) = 2x, de plus v(x) > 0
Z1
Z1 ′
2x
v (x)
pour tout x de [0 ; 1].
d
x
=
d x = [ln (v(x))]10 = ln(2). On en déduit que
2
0 1+x
0 v(x)
π 1
I0 = − ln(2).
4 2
Amérique du Nord
3
31 mai 2012
A. P. M. E. P.
Baccalauréat S
2.
a. Pour tout x de [0 ; 1], 0 6 x n et 0 6 f (x), donc 0 6 x n f (x) d’après la positivité de
Z1
x n f (x)d x, donc 0 6 In .
l’intégrale, on a 0 6
0
π
π
b. Pour tout x de [0 ; 1], 0 6 x n et f (x) 6 , donc x n f (x) 6 x n d’après la croissance
4
4
·
Z1
Z1
n+1 ¸1
π
π
x
π
=
xn d x =
×
, donc In 6
x n f (x)d x 6
de l’intégrale, on a
4 n + 1 0 4(n + 1)
0 4
0
π
.
4(n + 1)
π
π
et lim
= 0, d’après le théorème des comparaisons
c. On a 0 6 In 6
4(n + 1) n→+∞ 4(n + 1)
des limites de suites, (In ) converge et sa limite est 0 .
E XERCICE 4
Pour les candidats n’ayant pas suivi l’enseignement de spécialité
5 POINTS
1. f (M) = M ⇐⇒ z = z 2 ⇐⇒ z 2 − z = 0 ⇐⇒ z(z − 1) = 0 ⇐⇒ z = 0 ou z = 1. On en déduit que
Γ1 = {O, Ω}.
Ãp
p !
³
³ π´
³ π ´´
p
p
π
2
2
= 2 cos − + i sin −
= 2e−i 4 .
−i
2.
a. a = 2 − i 2 = 2
2
2
4
4
³p
´
π 2
π
b. Soit M tel que f (M) = A ⇐⇒ z 2 = a ⇐⇒ z 2 − 2e−i 4 = 0 ⇐⇒ z 2 − 2e−i 8 = 0 ⇐⇒
´³
´
³
p
p
p
p
p
π
π
π
π
π
z − 2e−i 8 z + 2e−i 8 = 0 ⇐⇒ z− 2e−i 8 = 0 ou z+ 2e−i 8 = 0 ⇐⇒ z = 2e−i 8 ou z =
p
π
− 2e−i 8 .
p
p
π
π
Les affixes des deux antécédents de A par f sont 2e−i 8 et − 2e−i 8 .
3. On pose z = x + iy l écriture algébrique de z. On a z ′ = x 2 − y 2 + 2ix y est imaginaire pur
si et seulement si x 2 − y 2 = 0 ⇐⇒ (x − y)(x + y) = 0 ⇐⇒ x − y = 0 ou x + y = 0 ⇐⇒ x =
y ou x = −y.
4.
5.
Γ2 est donc la réunion des droites d’équations x = y et x = −y.
a. M distinct de Ω est tel que le triangle ΩMM′ est rectangle isocèle direct en Ω si et
seulement si z 6= 1 et M′ est l’image de M par la rotation de centre Ω et d’angle
π
π
⇐⇒ z ′ − 1 = ei 2 (z − 1) ⇐⇒ z 2 − 1 = i(z − 1) ⇐⇒ z 2 − iz − 1 + i = 0 avec z 6= 1.
2
b. (z − 1)(z + 1 − i) = z 2 + z − iz − z − 1 + i = z 2 − iz − 1 + i
c. z 2 − iz − 1 + i = 0 ⇐⇒ (z − 1)(z + 1 − i) = 0 ⇐⇒ z − 1 = 0 ou z + 1 − i = 0 ⇐⇒ z = 1 ou
z = −1 + i. Or z 6= 1, donc Γ3 contient uniquement le point d’affixe −1 + i.
µ ′¶
µ 2¶
³−−→ −−−→´
z
z
′
a. OM , OM = arg
= arg
= arg(z).
z
z
³−−→ −−−→´
b. Les points O, M et M′ sont alignés si et seulement si OM , OM′ ≡ 0[π] ⇐⇒ arg(z) ≡
0[π] ⇐⇒ z ∈ R. Γ4 est donc l’axe des abscisses privé des points O et Ω.
Amérique du Nord
4
31 mai 2012
A. P. M. E. P.
Baccalauréat S
E XERCICE 4 S PÉCIALITÉ
5 POINTS
PARTIE A.
1. Recherche de points invariants :
M est un point invariant ⇐⇒ z = 5iz + 6i + 4 ⇐⇒ z − 5iz = 6i + 4 ⇐⇒ z(1 − 5i) = 6i + 4 ⇐⇒
6i + 4
z=
= −1 + i. L’unique point invariant par S est le point Ω d’affixe ω = −1 + i.
1 − 5i
¡
¢
′
′
z −ω = z −(−1+i) = 5iz +6i+4−(−1+i) ⇐⇒ z ′ −(−1+i) = 5iz +5+5i = 5i z ′ − (−1 + i) =
π
π
5ei 2 (z −ω) ⇐⇒ z ′ −ω = 5ei 2 (z −ω). C’est l’expression complexe de la similitude de centre
π
Ω, de rapport 5 et d’angle .
2
2. z ′ = x ′ + iy ′ = 5iz + 6i + 4 = 5i(x + iy) + 6i + 4 = 5ix − 5y + 6i + 4 = −5y + 4 + i(5x + 6) ⇐⇒
(
x ′ = −5y + 4
y ′ = 5x + 6
PARTIE B.
1.
2.
a. On a 4 × 1 + 3 × (−1) = 1, en multipliant par 5, on obtient 4 × 5 + 3 × (−5) = 5. On a
ainsi une solution particulière (5 ; −5). D’où 4a + 3b = 5 ⇐⇒ 4a + 3b = 4 × 5 + 3 ×
(−5) ⇐⇒ 4a − 4 × 5 = −3b + 3 × (−5) ⇐⇒ 4(a − 5) = −3(b + 5). On en déduit que 4
divise −3(b + 5), or 4 et -3 sont premiers entre eux, d’près le théorème de Gauss,
4 divise b + 5, donc ∃k ∈ Z tel que b + 5 = 4k ⇐⇒ b = −5 + 4k, on en déduit que
4(a − 5) = −3(−5 + 4k + 5) ⇐⇒ 4(a − 5) = −3 × 4k ⇐⇒ a − 5 = −3k ⇐⇒ a = 5 − 3k.
L’ensemble des couples solutions est donc {(5 − 3k ; −5 + 4k)/k ∈ Z}.
b. −3x ′ + 4y ′ = 37 ⇐⇒ −3x ′ + 4y ′ ⇐⇒ −3(−5y + 4) + 4(5x + 6) = 37 ⇐⇒ 20x + 15y − 12 +
(
x = 5 − 3k
24 = 37 ⇐⇒ 20x + 15y = 25 ⇐⇒ 4x + 3y = 5 ⇐⇒ ∃k ∈ Z tel que
y = −5 + 4k
−3 6 5−3k 6 5 et −3 6 −5+4k 6 5, donc seuls k = 1 et k = 2 sont tels que −3 6 x 6 5
et −3 6 y 6 5. Les points de coordonnées (2 ; −1) et (−1 ; 3) répondent à la question.
a. x ′ + y ′ = −5y + 4 + 5x + 6 = 5(x − y + 2), donc x ′ + y ′ est un multiple de 5.
b. x ′ + y ′ − (x ′ − y ′ ) = 2y ′ , donc x ′ − y ′ et x ′ + y ′ sont congrus modulo 2.
Par ailleurs 2 est un nombre premier. Si 2 divise x ′2 − y ′2 = (x ′ − y ′ )(x ′ + y ′ ), alors il
divise x ′ − y ′ ou x ′ + y ′ . Supposons qu’il divise x ′ − y ′ , alors x ′ − y ′ ≡ 0 [2], or x ′ − y ′ ≡
x ′ + y ′ [2], donc x ′ + y ′ ≡ x ′ − y ′ ≡ 0 [2]. Le raisonnement est identique si on suppose
que x ′ + y ′ ≡ 0 [2].
c. x ′2 − y ′2 = 20 donc x ′2 − y ′2 est multiple de 2 donc x ′ − y ′ et x ′ + y ′ le sont également.
Par ailleurs x ′ + y ′ est un multiple de 5. Or (x ′ − y ′ )(x ′ + y ′ ) = 20, donc x ′ + y ′ est un
multiple de 2 et de 5 qui divise 20, x ′ + y ′ est donc un multiple de 10 qui divise 20.
On en déduit que x ′ + y ′ = ±10 ou x ′ + y ′ = ±20. x ′ + y ′ = ±20 est impossible car cela
donnerait x ′ − y ′ = ±1 qui ne serait pas congru à x ′ + y ′ = ±20 modulo 2. Il reste donc
l’unique possibilité x ′ + y ′ = ±10 donc x ′ − y ′ = ±2, ce qui donne x ′ = ±6 et y ′ = ±4.
2
x ′ = 6 n’est pas possible car cela donnerait 6 = −5y + 4 d’où y = − , donc y n’est
5
pas entier. On a finalement x ′ = −6 et y ′ = −4 ce qui donne x = −2 et y = 2. L’unique
point de E est donc (2 ; −2).
Amérique du Nord
5
31 mai 2012