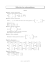1. Calcul du po

La diagonalisation sur un exemple
M0SE 1003
Dans cette fiche, on détaille les 4 étapes de la diagonalisation :
1. Calcul du polynôme caractéristique et recherche de ses racines.
2. Diagnostique : diagonalisable ou pas ?
3. Recherche de vecteurs propres associés aux valeurs propres trouvées à l’étape 1.
4. Conclusion : expression de la matrice sous la forme P × D × P −1 , et éventuellement, vérification.
sur les matrices
B=
3 0
4 −1
0 1
C=
D=
0 3
1 2
2 1
de l’exercice 12 de la feuille 2.
1. Calcul du polynôme caractéristique et recherche de ses racines.
• χ(B) = λ2 − 6λ + 9 = (λ − 3)2 . Le polynôme caractéristique de B a une racine double, λ = 3.
• χ(C) = λ2 − 6λ + 9 = (λ − 3)2 . Le polynôme caractéristique de C a une racine double, λ = 3.
• χ(D) = λ2 − λ − 2. On calcule le discriminant ∆(χ(D)) = 1 − 4 × 1 × (−2) = 9. Le polynôme
caractéristique de D a deux racines, λ1 = 1−3
= −1 et λ2 = 1+3
= 2.
2
2
2. Diagnostique : diagonalisable ou pas ?
• La matrice B est diagonale... elle est donc en particulier diagonalisable et déjà diagonalisée ! Il n’y
a plus rien à faire. (On aurait d’ailleurs bien pu se passer de calculer χ(B) mais bon, c’était pour
l’exemple).
• Le polynôme caractéristique de C n’a qu’une seule racine double, et C n’est pas une matrice
diagonale. C n’est donc pas diagonalisable (dernier théorème de votre cours, ou dernière proposition
p. 21 de mes notes de cours).
• χ(D) a deux racines distinctes. D est donc diagonalisable, et possède deux valeurs propres distinctes,
= −1 et λ2 = 1+3
= 2.
λ1 = 1−3
2
2
1
La diagonalisation sur un exemple
M0SE 1003
3. Recherche de vecteurs propres associés aux valeurs propres trouvées à l’étape 1.
On n’a donc ici plus que D à traiter.
Recherche d’un vecteur propre X1 associé à la valeur propre λ1 = −1.
Un tel vecteur est une solution du système (D − λ1 .I2 )X = 0
0 1
1 0
0 − (−1)
1
⇔
− (−1) ×
X=0 ⇔
X=0
2 1
2
1 − (−1)
0 1 1 1
x
0
x+y = 0
x = −y
⇔
=
⇔
⇔
2 2
y
0
2x + 2y = 0
0 = 0
1
Par exemple, le vecteur X1 =
convient.
−1
Recherche d’un vecteur propre X2 associé à la valeur propre λ2 = 2.
Un tel vecteur est une solution du système (D − λ2 .I2 )X = 0
0 1
1 0
0−2
1
⇔
−2×
X=0 ⇔
X=0
2 1
1−2
0 1 2
−2 1
x
0
−2x + y = 0
2x = y
⇔
=
⇔
⇔
2 −1
y
0
2x − y = 0
0 = 0
1
Par exemple, le vecteur X2 =
convient.
2
4. Conclusion
−1 0
1 1
P −1 , où la matrice P = (X1 |X2 ) =
.
0 2
−1 2
2 −1
On peut vérifier qu’on ne s’est pas trompé en calculant P −1 = 13
, d’où
1 1
1 −2 1
1 1 1
1 0 3
−1 0
−1 0
−2 1
P −1 =
et finalement P
P −1 =
=
= D.
0 2
0 2
2 2
3 2 2
3 −1 2
3 6 3
D s’écrit donc D = P
2