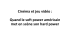Corrigé

Introduction à la Finance Quantitative
Feuille d’exercices 1 — Corrigé
Exercice 1
1. Il protège contre les risque de hausse et de baisse de l’actif (comme un call pour les hausses et
comme un put pour les baisses).
2. On obtient le même payoff en achetant un call de strike 120 et un put de strike 100. Cela
correspond à ajouter les deux payoffs correspondants, ce qui produit la figure.
3. Ce contrat donne donc le droit d’acheter le sous-jacent au prix 120 à l’échéance ou de le vendre
au prix 100 à l’échéance.
Exercice 2
1. (S1 (T ) − K)+ .
2. Il s’agit d’un call américain.
Exercice 3
On trouve qu’une probabilité risque neutre (PRN) ou une mesure de valorisation universelle
(MVU) (q1 , q2 , q3 ) est solution de
q3 = 5r + q1 ,
q2 = 1 − 5r − 2q1 ,
où q1 est un paramètre libre. Pour obtenir une PRN, il faut que q2 soit strictement positif,
donc r < 1/5, et si c’est le cas, alors on trouve une PRN en choisissant q1 > 0 suffisamment
petit. De même, il existe une MVU pour r 6 1/5. Enfin, pour la loi du prix unique, on cherche
les stratégies H telles que V1 = X pour une variable aléatoire X arbitraire, et la loi du prix
unique sera satisfaite si toutes ces stratégies ont même valeur initiale. Ici, on vérifie facilement
qu’il y a au plus une seule stratégie qui convient. Finalement
• il existe une PRN ssi 0 < r < 0.2 (et donc une MVU et la loi du prix unique est satisfaite),
• il existe une MVU mais pas de PRN ssi r = 0.2 (et la loi du prix unique est satisfaite),
• sinon, seule la loi du prix unique est satisfaite.
Exercice 4
1. Q =
1 3 7
11 , 11 , 11
2. On trouve
.
28
11 .
3. Il y en a une seule : H = (−12, 2, 1).
1
Exercice 5 : formule de parité call-put
1. La formule de parité call-put est indépendante du modèle. Elle se démontre comme suit : si le
payoff est duplicable, on obtient pour le call
X
(S1 (1) − K)+
C = EQ
= EQ
S0 (1)
S0 (1)
et pour le put
P = EQ
(K − S1 (1))+
S0 (1)
En utilisant la relation (x)+ − (−x)+ = x, on obtient
(S1 (1) − K)+ − (K − S1 (1))+
S1 (1) − K
K
C − P = EQ
= EQ
= EQ [S1∗ (1)] −
.
S0 (1)
S0 (1)
1+r
Le résultat demandé est alors une conséquence de la définition d’une probabilité risque neutre.
2. Il suffit de montrer que, lorsqu’un call (ou un put) est duplicable, alors le put (ou le call) de
même strike est forcément duplicable aussi. Soit H une stratégie duplicant le call. On pose
alors
K
, −1 .
Ĥ = H +
1+r
La richesse terminale correspondant à ce portefeuille est
V̂1 = V1 +
K
S0 (1) − S1 (1) = (S1 (1) − K)+ − (S1 (1) − K) = (K − S1 (1))+ ,
1+r
où la dernière égalité vient de la relation (x)+ − (−x)+ = x déjà utilisée. On a donc bien trouvé
une stratégie qui replique le payoff du put, et la question est résolue. De nouveau, on remarque
que ce résultat est indépendent du modèle considéré.
Exercice 6
1. On trouve Q = (q1 , 2 − 3q1 , 2q1 − 1), où q1 est un paramètre libre. Pour que ce soit une PRN,
il faut que toutes les coordonnées soient strictement positives, soit q1 ∈] 21 , 23 [. Il y a donc une
infinité de PRN.
2. Avec la formule de la question précédente, on doit avoir 8q1 + 11(2 − 3q1 ) + 14(2q1 − 1) = 10
(c’est la même équation pour les MVU). On obtient q1 = 23 , q2 = 0, q3 = 41 . Il n’y a donc pas
de PRN, mais il y a une unique MVU.
3. Il existe donc une opportunité d’arbitrage, mais pas de stratégie dominante. Ici, il est plus
difficile de donner une méthode générale pour cette question. C’est plus l’observation du tableau
de prix qui peut permettre de trouver la solution. Ici, on remarque que l’actif 1 fait +1 sur le
premier scenario et −2 sur le troisième, alors que l’actif 2 fait −2 sur le premier scenario et +4
sur le troisième. Ainsi, 2S1 + S2 est constant sur ω1 et ω3 , donc cela suggère une opportunité
d’arbitrage de la forme H = (x, 2, 1) ou H = (x, −2, −1) avec x choisi tel que V0 = 0. On
trouve finalement que H = (22, −2, −1) est une opportunité d’arbitrage.
2