Première STMG - Fonction dérivée d`une fonction

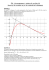
Fonction dérivée d’une fonction polynôme
de degré deux
I) Fonction dérivée d’une fonction polynome de degré
deux
Soit
une fonction polynôme de degré 2 définie sur
:
La fonction dérivée de , notée ’, est la fonction définie sur
par :
′
Exemples :
Exemple 1:
Soit
Exemple 2:
Soit
6
5
Alors
Alors
Exemple 3:
Exemple 4:
Soit
5
2
Alors
5
3
Soit
6
3
7
7
2
4
1
4
Alors
′
II) Application à l’étude des variations d’une fonction
1) Théorème
Soit
une fonction polynôme de degré 2:
pour tout d’un intervalle I, alors est croissante sur cet
• Si
intervalle.
pour tout
• Si
intervalle.
d’un intervalle I, alors
est décroissante sur cet
Exemples :
Exemple 1:
Soit
6
Alors
0 a pour solution 2
0 soit
1
∞
∞
Signe
de ′
0
1
2
0 sur ] ∞ ;
1
2
0 sur [ ;
] donc
est décroissante sur cet intervalle
∞ [ donc
est croissante sur cet intervalle
On obtient le tableau de variation suivant :
∞
∞
Signe de ′
0
6,25
1
2
6,25 (Résultat que nous pouvons obtenir à partir de la calculatrice)
Exemple 2:
Soit
Alors
5
2
0 pour
0 soit
2
=0
0 sur] ∞ ; 0 ] donc
est croissante sur cet intervalle
0 sur [0 ;
est décroissante sur cet intervalle
∞ [ donc
On obtient le tableau de variation suivant :
∞
Signe de ′
0
0
5
0
5
∞
Exemple 3:
Soit
5
3
6
Alors
0 pour
10
3
0 soit
= 0,3
0 sur] ∞ ; 0,3 ] donc
est croissante sur cet intervalle
0 sur [0,3 ;
est décroissante sur cet intervalle
∞ [ donc
On obtient le tableau de variation suivant :
∞
Signe de ′
0,3
∞
0
5,55
0,3
5,55 (Résultat que nous pouvons obtenir à partir de la calculatrice)