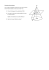Télécharger

Correction Brevet Mathématiques 2014 Pondichéry - Série
générale
Exercice 1
1. Arthur veut répartir ces dragées de façon identique dans 20 corbeilles. Pour que la
répartition soit égale entre chaque corbeille il faut faire la division avec reste de 3003 par 20 et de
3731 par 20. Or
3003 = 20 × 150 + 3,
3731 = 20 × 186 + 11.
Donc Arthur peut faire 20 corbeilles contenant chacune 150 dragées au chocolat et 186 dragées aux
amandes. Dans ce cas, il lui restera 3 dragées au chocolat et 11 dragée aux amandes.
2. (a) 90 ne divise pas 3003, ils ne peuvent donc pas faire 90 ballotins de composition identiques sans
qu’il reste des dragées au chocolat.
(b) Pour qu’il ne reste pas de dragée, il faut que le nombre de ballotins soit un diviseur de 3003 et de
3731, on cherche donc un diviseur commun à 3003 et 3731. Par ailleurs, s’ils veulent faire un
maximum de ballotin cela signifie que l’on recherche le plus grand diviseur commun à 3003 et
3731. On applique alors l’algorithme d’Euclide à 3003 et 3731 :
3731 = 3003 × 1 + 728,
3003 = 728 × 4 + 91,
728 = 91 × 8 + 0.
Donc d’après l’algorithme d’Euclide, le PGCD de 3003 et 3731 étant le dernier reste non nul
nous obtenons PGCD(3003, 3731) = 91.
Donc Arthur et Emma peuvent faire au maximum 91 ballotins donc la composition est identique
s’il ne doit pas leur rester de dragées.
En outre, pour trouver la composition des ballotins, vu que les dragées sont équitablement
répartis on obtient que le nombre de dragées au chocolat sera de :
3003/91 = 33,
et celui de dragées aux amandes sera de :
3731/91 = 41.
Donc Emma et Arthur peuvent au maximum faire 91 ballotins identiques, sans qu’il leur reste de
dragées, qui seront chacun composé de 33 dragées au chocolat et de 41 dragées aux amandes.
Exercice 2 Dans cet exercice nous donnerons les justifications pour vous permettre de comprendre la
réponse, mais vu la consigne il n’était pas nécessaire de le faire sur votre copie, vous n’aviez qu’à recopier
la réponse exacte.
1
1.
p
(−5)2 est égal à 5.
En effet,
q
√
(−5)2 = 25 = 5.
2. Si deux surfaces ont la même aire alors leurs périmètres ne sont pas forcément égaux.
Par exemple, le carré de côté 1 cm aura une aire égale à 1 cm2 . Par ailleurs son périmètre sera de
1 + 1 + 1 + 1 = 4 cm.
Le rectangle dont la longueur est égale à 2 cm et la largeur 0, 5 cm aura lui aussi une aire de
2 × 0, 5 = 1 cm2 . Pourtant son périmètre est de 2 + 0, 5 + 2 + 0, 5 = 5 cm. Donc nous avons deux
surface (celle du carré et celle du rectangle) de même aire mais de périmètres différents.
3. Soit f la fonction définie par f (x) = 3x − (2x + 7) + (3x + 5), f est une fonction affine.
En effet si l’on développe dans l’expression de f l’on obtient,
f (x) = 3x − 2x − 7 + 3x + 5 = 4x − 2.
Pour tout x, f est de la forme ax + b avec a et b non nul, c’est donc bien une fonction affine.
4. L’enquête ne peut pas l’aider.
En effet les tirages du loto ne dépendent pas des précédents tirages puisque les numéros sont tirés au
hasard.
5. Une expression factorisée de (x − 1)2 − 16 est (x + 3)(x − 5).
En effet,
(x − 1)2 − 16 = (x − 1)2 − 42 = ((x − 1) − 4) ((x − 1) + 4) = (x − 1 − 4)(x − 1 + 4) = (x − 5)(x + 3).
Exercice 3 Nous allons chercher à appliquer les étapes de calcul décrites dans la phrase à n’importe quel
entier pour voir si c’est toujours un multiple de 10 ou pas.
Prenons alors n un nombre entier.
Je lui ajoute 3, j’obtiens alors maintenant le nombre entier n + 3.
Puis je le multiplie par 7 donc j’obtiens le nombre entier 7(n + 3) = 7n + 21.
Puis j’ajoute le triple du nombre de départ, soit 3n au résultat c’est à dire à 7n + 21, j’obtiens alors
3n + 7n + 21 = 10n + 21.
Enfin, j’enlève 21 au nombre obtenu donc 10n + 21 − 21 = 10n.
Le nombre que j’obtiens à la fin des étapes décrites pour un entier n choisi au départ est l’entier 10n c’est
bien alors un multiple de 10. Donc, quel que soit l’entier que je choisi au départ, j’obtiens toujours un
multiple de 10.
Exercice 4 Nous allons calculer la longueur des deux parcours.
Pour le parcours ACDA :
longueurACDA = AC +CD + DA = 1, 4 km + 1, 05 km + DA.
Il faut donc que l’on calcule DA pour obtenir la longueur du parcours ACDA. Or, puisque les codages sont
corrects, le triangle ACD est rectangle en C. Donc, d’après le théorème de Pythagore, on obtient que
DA2 = CD2 + AC2 ,
donc,
DA2 = (1, 05)2 + (1, 4)2 ,
donc,
DA2 = 3, 0625,
2
donc, comme DA est une longueur donc est positive,
p
DA = 3, 0625 = 1, 75 km.
Donc,
longueurACDA = 1, 4 km + 1, 05 km + 1, 75 km = 4, 2 km.
De même, pour le parcours AEFA :
longueurAEFA = AE + EF + FA = 1, 3 km + EF + 1, 6 km.
Il faut donc que l’on calcule EF pour obtenir la longueur du parcours AEFA. Or, puisque les codages sont
corrects, les droites (E 0 F 0 ) et (EF) sont parallèles, de plus les points A, E 0 et E ne sont pas confondus ainsi
que les points A, F 0 et F. Et les droites (E 0 E) et (F 0 F) sont sécantes en A. Donc d’après le théorème de
Thalès :
AE 0 AF 0 E 0 F 0
=
=
,
AE
AF
EF
donc
E 0 F 0 AE 0
=
,
EF
AE
donc,
0, 4 0, 5
=
,
EF
1, 3
donc
1, 3
EF = 0, 4 ×
= 1, 04 km.
0, 5
Donc
longueurAEFA = 1, 3 km + 1, 04 km + 1, 6 km = 3, 94 km.
On en conclut donc que le parcours dont la longueur s’approche le plus de 4 km est le parcours AEFA. La
commune devrait donc choisir ce parcours.
Exercice 5
1. Le volume d’un cylindre a pour formule aire de la base×hauteur.
Un cylindre a pour base un cercle, et dans notre cas le cercle a pour diamètre 10 cm donc c’est un
cercle de rayon 5 cm. Appelons Vc le volume de la partie cylindrique de la bouteille. Donc comme
aire de la base = pi × 52 = 25π cm2 ,
alors la partie cylindrique de la bouteille a pour valeur de volume exacte :
Vc = 25π × 15 = 375π cm3 .
Donc la partie cylindrique de la bouteille a pour valeur de volume approchée :
Vc ≈ 1178 cm3 .
2. (a) V1 a pour expression :
aire base grand cône × SO
.
3
Or, le rayon de la base du grand cône est de 5 cm donc,
V1 =
aire base grand cône = 52 × π = 25π cm2 .
Donc
V1 =
25π × 6 150π
=
= 50π cm3 .
3
3
3
(b) Pour obtenir le tronc de cône, on a coupé le grand cône par un plan parallèle à la base passant
par O0 . Donc le petit de cône, de base de centre O0 parallèle à la base du grand cône et de hauteur
SO0 est une réduction du grand cône. Le coefficient de réduction est donnée par le rapport
SO0 2 1
= = .
SO
6 3
1
Donc le petit cône est une réduction du grand cône de coefficient . Donc par rapport au grand
3
cône toute ses longueurs sont divisées par 3, sa surface est divisée par 32 = 9 et son volume par
33 = 27.
Donc le volume du petit cône
V1 50π 3
=
cm .
V10 =
27
27
Par ailleurs le volume du tronc de cône est :
V2 = V1 −V10 = 50π −
50π
1350π − 50π
1300π 3
=
=
cm .
27
27
27
Donc
V2 ≈ 151 cm3 .
3. V (h) correspond au volume de liquide présent dans la bouteille en fonction de la hauteur h de
remplissage de la bouteille.
Nous allons procéder par élimination. On peut déjà éliminer le graphique 2, en effet le volume de
liquide présent augmente lorsque la hauteur de liquide dans la bouteille augmente, il ne peut pas
redescendre.
Ensuite pour éliminer d’autres graphiques nous allons calculer le volume V qu’il peut y avoir dans
la bouteille lorsqu’elle est remplie.
Or,
V = Vc +V2 ≈ 1329 cm3 .
Donc ce ne peut être ni le graphique 3, ni le graphique 4 car dans ces deux graphiques le volume
final V (h) est supérieur à V , ce qui est impossible puisque V est le volume de la bouteille pleine.
Donc le graphique donnant V (h) en fonction de h est le graphique 1.
Exercice 6
1. On a saisie dans la cellule O2 la formule = Somme(B2 : N2).
2. (a) La moyenne de cette série se calcule en faisant :
8 × 1 + 2 × 2 + 2 × 3 + 2 × 4 + 5 + 3 × 6 + 11 + 2 × 13 + 14 + 15 + 18 + 32 + 40 205
=
≈ 8.
26
26
Donc la moyenne de cette série arrondi à l’unité près est de 8.
(b) Il y a 26 valeurs dans cette série la médiane est donc la moyenne de la 13ème valeur et de la
14ème. Or la 13ème valeur et la 14ème sont toutes les deux de 4, donc la médiane de cette série
est de 4.
(c) Les valeurs prises par la médiane et la moyenne sont différentes car un grand nombre de pays
a gagné un petit nombre de médailles d’or, il est donc normal que la médiane soit peu élevée.
Cependant, certains pays ont gagné beaucoup de médailles comparés aux autres, ils ont donc fait
augmenter la moyenne ce qui explique qu’elle soit plus élevée que la médiane.
3. Soit x le nombre total de pays médaillés aux jeux olympiques pour le cyclisme masculin. Il y a 26
pays qui ont obtenus au moins une médaille d’or or cela représente 70% des pays participants. Donc
70
x = 26,
100
4
donc,
10 260
=
.
7
7
Donc le nombre total de pays médaillés est d’environ (arrondi à l’unité près) :
x = 26 ×
x ≈ 37 pays.
Donc comme il y a 26 pays médaillés d’or et qu’il y a au total 37 pays, il y a donc 11 pays qui n’ont
obtenu que des médailles d’argent ou de bronze.
5