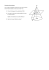Boule inscrite dans un cône de volume minimal 1 Enoncé : on

Boule inscrite dans un cône de volume minimal
Enoncé : on cherche à déterminer la hauteur d’un cône contenant une boule de
rayon r tel que le volume du cône soit minimal.
Correction
On note AO = x, OH = r, EC = R et h = AE
π
π
Le volume du cône est donné par V(x) = ×EC²×AE = ×R²×h
3
3
En appliquant le théorème de Pythagore dans les 4 triangles rectangle AHO,
AEC, OHC et OEC, on obtient :
•
AO² = AH² + OH² soit : x² = AH² + r²
(1)
•
AC² = AE² + EC² soit : AC² = (x + r)² + R²
(2)
•
OC² = OH² + HC² soit OC² = r² + HC²
(3)
•
OC² = OE² + EC² soit OC² = r² + R²
(4)
On a de plus :
AH + HC = AC
(5)
Des équations (3) et (4), on déduit que HC = R.
(2) et (5)
R² = AC² - (x + r)² = (AH + HC)² - (x + r)²
Soit R² = (AH + R)² - (x + r)² = AH² + 2×AH×R + R² - (x + r)²
0 = AH² + 2×AH×R – (x + r)²
Soit R =
1
Boule inscrite dans un cône de volume minimal
Soit R =
(x + r)² - AH²
2AH
(1)
AH =
(6)
x² - r²
D’où en reportant dans (6) : R =
Soit R =
x² + 2xr + r² - x² + r²
2 x² - r²
(x + r)² - (x² - r²)
2 x² - r²
=
2r² + 2xr
2 x² - r²
=
r( x + r)
x+r x-r
= r×
x+r
x-r
x+r
(x + r)²
π
π
π
Donc V(x) = ×R²×h = ×r²×
×(x + r) = ×r²×
3
3
3
x-r
x-r
u(x)
π
V(x) = k×
avec k = ×r² (une constante) et u(x) = (x + r)² et v(x) = x – r.
3
v(x)
u’(x)v(x) – u(x)v’(x)
V’(x) = k×
(v(x))²
Or u’(x) = 2(x + r) et v’(x) = 1
2(x + r)(x – r) – (x + r)² π
2x – 2r – x – r
π
Donc V’(x) = ×r×
= ×r×(x + r)×
3
3
(x – r)²
(x – r)²
x – 3r
π
Soit V’(x) = ×r×(x + r)
3
(x – r)²
Etude du signe de V’(x) :
Comme x > 0 et r > 0, V’(x) est du signe de x – 3r et s’annule donc pour x = 3r.
V est décroissante sur [0 ;3r] et croissante sur [3r ;+ ∞[.
V admet un minimum pour x = 3r.
La hauteur du cône est alors h = x + r = 4r.
2