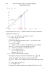DEVOIR À LA MAISON NO 5 : CORRIGÉ

© Laurent Garcin
MPSI Lycée Jean-Baptiste Corot
D EVOIR
À LA MAISON N O
5:
CORRIGÉ
Problème 1 — Fonction Γ
Partie I –
1. ∀t > 0, ga (t) = ea ln t .
Si a > 0, lim a ln(t) = −∞ et donc lim ga (t) = 0.
t→0
t→0
Si a = 0, alors ∀t > 0, ga (t) = 1 et donc lim ga (t) = 1.
t→0
Ainsi, dans tous les cas, ga a une limite finie en 0. Elle est donc prolongeable par continuité en 0 en posant ga (0) = 0
pour a > 0, ou g0 (0) = 1.
a
Soit a > 1. Sur ]0; +∞[, ga est de classe C 1 et ∀t > 0, ga0 (t) = ta = ata−1 = aga−1 (t).
t
Or a > 1 et donc ga0 a une limite finie en 0 (voir étude de ga ).
Ainsi g est continue sur [0; +∞[, ga est de classe C 1 sur ]0; +∞[ et ga0 a une limite finie en 0.
Alors, par application du théorème du prolongement C 1 , ga est de classe C 1 sur [0; +∞[ et ga0 = aga−1 .
2. t 7→ 1 − t est continue sur [0, 1] à valeur dans [0, 1] et gb est continue sur [0, 1] donc t 7→ gb (1 − t) est continue
sur [0; 1] comme composée de fonctions continues. Alors I(a, b) est l’intégrale au sens de Riemann de la fonction
t 7→ ga (t)gb (1 − t) continue sur [0; 1].
Z0
Posons u = 1 − t. Alors I(a, b) = ga (1 − u)gb (u)(−du) = I(b, a).
1
Z1
ga+1 (t)gb (t)dt, avec ga+1 et gb+1 de classe C 1 sur [0; 1]. Intégrons alors par parties :
3. I(a + 1, b) =
0
ï
I(a + 1, b) = −
1 a+1
t
(1 − t)b+1
b+1
ò1
a+1
+
b+1
0
Z1
ta (1 − t)b+1 dt
0
a + 1 et b + 1 sont supérieurs à 1, on déduit ga+1 (0) = gb+1 (0) = 0. Ainsi I(a + 1, b) =
a+1
I(a, b + 1) ou encore
b+1
I(a + 1, b)
I(a, b + 1)
=
.
a+1
b+1
Z1
ta dt =
4. Tout d’abord, pour tout a ∈ R+ , I(a, 0) =
0
1
. On formule l’hypothèse de récurrence suivante :
a+1
Pn : ∀a ∈ R+ , I(a, n) =
n!
(a + 1)(a + 2) · · · (a + n + 1)
1
Tout d’abord, P0 est vraie puisque I(a, 0) = a+1
pour tout a ∈ R+ . Supposons Pn vraie pour un certain n ∈ N.
Soit alors a ∈ R+ . D’après la question précédente,
I(a, n + 1) =
n+1
I(a + 1, n)
a+1
et d’après Pn 1 ,
I(a + 1, n) =
n!
(a + 2)(a + 3) · · · (a + n + 2)
1. Notez l’importance du «∀a ∈ R+ » dans cette hypothèse de récurrence
http://lgarcin.github.io
1
© Laurent Garcin
MPSI Lycée Jean-Baptiste Corot
Il en découle que
I(a, n + 1) =
(n + 1)n!
(n + 1)!
=
(a + 1)(a + 2)(a + 3) · · · (a + n + 2)
(a + 1)(a + 2) · · · (a + n + 2)
Ainsi Pn+1 est-elle vraie.
Par récurrence, Pn est vraie pour tout n ∈ N.
5. Pour p et q entiers naturels,
q!
p!
q!
p!q!
I(p, q) =
=
=
.
(p + 1)(p + 2) · · · (p + q + 1)
p! (p + 1) · · · (p + q + 1)
(p + q + 1)!
6. Posons u = sin2 θ ; alors du = 2 sin θ cos θdθ et (cos θ)2q = (cos2 θ)q = (1 − u)q .
Z
1
1 1 p
u (1 − u)q du = I(p, q).
Donc J(p, q) =
2 0
2
Z π2
(sin θ)2p+1 (cos θ)2q+1 dθ =
0
p!q!
1
·
2 (p + q + 1)!
Partie II –
a
x−a
> 0 i.e. pour x tel que
> 0.
x
x
Donc fa est définie sur ] − ∞; 0[∪]a; +∞[
Å
ã
x
a
a
− pour x > a.
2. Posons ϕ(x) = ln x − ln(x − a) − = ln
x
x−a
x
Pour x > a,
1
a
x(x − a) − x2 + a(x − a)
a2
1
+ 2 =
=
−
<0
ϕ 0 (x) = −
x x−a x
x2 (x − a)
x2 (x − a)
1. fa (x) est défini pour x tel que 1 −
donc ϕ décroît strictement sur ]a; +∞[.
x
a
Or lim
= 1 et lim
= 0 conduisent à lim ϕ(x) = 0.
x→+∞ x − a
x→+∞ x
x→+∞
x
Des variations de ϕ et de sa limite en +∞ on conclut ϕ(x) > 0 i.e. ln(x) − ln(x − a) > pour tout x > a.
a
Å
ã
a
x
a
Reprenons la même démarche avec ψ : x 7→ ln x − ln(x − a) −
= ln
−
.
x−a
x−a
x−a
Pour x > a,
1
1
a
a2
ψ 0 (x) = −
+
=
>0
2
x x − a (x − a)
x(x − a)2
donc ψ croît strictement sur ]a; +∞[.
On démontre de même que précédemment que lim ψ(x) = 0.
x→+∞
a
pour tout x > a.
x−a
Remarque. De manière plus expéditive, on peut utiliser l’inégalité classique ln(1 + u) 6 u valable pour tout
u ∈] − 1, +∞[. Alors pour tout x ∈]a, +∞[,
a x
ln(x) − ln(x − a) = − ln 1 −
>
x ã a
Å
a
a
ln(x) − ln(x − a) = ln 1 +
6
x−a
x−a
Ainsi ψ croît sur ]a, +∞[ et a pour limite 0 en +∞, donc ψ(x) 6 0 i.e. ln(x) − ln(x − a) 6
3. fa est dérivable sur ]a; +∞[ et pour x > a,
fa0 (x) = ln(x − a) − ln(x) +
a
>0
x−a
Ainsi fa croît sur ]a; +∞[.
ax
De plus, pour tout x > a, fa (x) = −x(ln(x) − ln(x − a) donc − x−a
6 fa (x) 6 −a d’après II.2. Par encadrement,
http://lgarcin.github.io
2
© Laurent Garcin
MPSI Lycée Jean-Baptiste Corot
lim+∞ fa = −a. Donc Ca admet pour asymptote horizontale la droite d’équation y = −a.
Il est clair que lima+ fa = −∞ donc Ca admet pour asymptote verticale la droite d’équation x = a.
On en déduit le tableau de variations :
x a
+∞
fa0
+
a
fa
−∞
4. On obtient le graphe suivant :
1
−1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
−1
C1
−2
C2
−3
C3
−4
−5
−6
−7
−8
−9
−10
5. Pour tout entier n > a, yn = exp (fa (n)). La fonction fa est croissante sur ]a; +∞[ à valeurs dans ] − ∞; −a[, et
exp est croissante sur R. Donc exp ◦fa croît sur ]a; +∞[. Ainsi la suite (yn ) est croissante .
Par ailleurs,
lim fa (n) = −a donc
n→+∞
lim yn = e−a .
n→+∞
Partie III –
u n
u n x
1. Soit h : u 7→ 1 −
u . h est continue sur [0; n] car h est la produit de la fonction polynôme u 7→ 1 −
par
n
n
la fonction gx étudiée dans la partie I. Donc Fn (x) est une intégrale de Riemann.
Z1
Z1
u
En effectuant le changement de variable t = , Fn (x) = (1 − t)n (nt)x ndt = nx+1 (1 − t)n tx dt = nx+1 I(x, n).
n
0
0
Å
ãn+1
u n
u
2. D’après la question II.5 pour u > 0, 1 −
6 1−
. Ce résultat est clairement vrai pour u = 0.
n
n+1
n
u
Or la fonction u 7→ 1 −
ux est positive sur [0; n + 1]. alors
n
Zn Å
Z n+1 Å
ãn+1
ãn+1
u
u
Fn (x) 6
1−
ux du 6
1−
ux du
n
+
1
n
+
1
0
0
Ainsi, pour x fixé, Fn (x) 6 Fn+1 (x) .
http://lgarcin.github.io
3
© Laurent Garcin
3.
a.
MPSI Lycée Jean-Baptiste Corot
lim ux+2 e−u = 0 (étude comparée des exponentielles et fonctions puissances).
u→+∞
Donc ∃U > 0, tq u > U =⇒ e−u ux+2 6 1 (prendre ε = 1 dans la définition de la limite nulle en +∞).
1
Ainsi ∃U > 0, ∀u ∈ R+ , u > U =⇒ e−u 6 x+2 .
u
u n
u b. Pour 0 < u < n, 1 −
.
= exp n ln 1 −
n
n
u
u
Or n ln 1 −
= n(ln(n − u) − ln(u)) 6 − · n = −u (voir inégalité de II.2).
n
n
u n
6 e−u . Remarquons que cette inégalité reste vraie pour u = n et pour u = 0.
Donc 1 −
n Zn
e−u ux du.
Alors Fn (x) 6
0
I Pour n > U,
ZU
Fn (x) 6
Zn
e
u du +
0
ZU
6
0
I Pour n < U, Fn (x) =
Rn
0
U
RU
0
x
ux+2
u du 6
1
1
e−u ux du + ( − ) 6
U n
e−u ux dx <
donc, ∀n ∈ N∗ , Fn (x) 6
ZU
1
−u x
RU
0
e−u ux du 6
e−u ux du +
RU
0
ZU
0
Zn
e
−u x
u du +
0
U
1
du
u2
1
e−u ux du +
U
e−u ux du +
1
U
1
.
U
c. Remarquons que U ne dépend pas de n (voir III.3.a)
ZU
e−u ux du +
Donc pour x fixé, la suite (Fn (x))n∈N∗ est majorée par la constante
0
1
.
U
Or cette suite est croissante (III.2). Cette suite croissante et majorée converge.
4. Soit x ∈ R+ fixé.
Fn (x + 1)
nx+2 I(x + 1, n)
III.1
x
+
1
= nx+2
I(x, n + 1)
I.3
n+1
nx+2
(n + 1)x+1 I(x, n + 1)
= (x + 1)
(n + 1)x+2
Å
ãx+2
n
= (x + 1)
Fn+1 (x)
III.1
n+1
=
ãx+2
n
= 1. Alors en faisant tendre n vers +∞, on obtient F(x + 1) = (x + 1)F(x) .
n→+∞ n + 1
Alors, pour k entier naturel, F(k) = k!F(0). Il reste donc à calculer F(0).
n!
n
Mais Fn (0) = nI(0, n) = n ·
=
. Donc F(0) = lim Fn (0) = 1.
n→+∞
(n + 1)!
n+1
Ainsi pour tout k ∈ N, F(k) = k!
Å
Or
lim
http://lgarcin.github.io
4