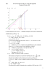Deux méthodes pour une suite

Deux méthodes pour une suite
3 x+2
.
x+4
1. Étudier les variations de f et en déduire que, pour tout x élément de I, f (x) appartient à I.
2. On considère la suite u définie par u0 = 0 et un+1 = f (un). Montrer que pour tout entier naturel n, un
appartient à I.
I est l'intervalle [0,1]. On considère la fonction f définie sur I par f ( x)=
On se propose d'étudier la suite u par deux méthodes différentes.
Première méthode
3. a) Représenter graphiquement f dans un repère orthonormal d'unité graphique 10 cm.
b) En utilisant le graphique précédent, placer les points A0, A1, A2 et A3 d'ordonnée nulle et
d'abscisses respectives u0, u1, u2 et u3.
Que suggère le graphique concernant le sens de variation de u et sa convergence ?
(1−un )(u n+2)
c) Établir la relation u n+1−u n=
et en déduire le sens de variation de la suite u.
u n+4
d) Démontrer que la suite u est convergente.
e) Prouver que la limite l de la suite u vérifie l = f (l) et calculer l.
Deuxième méthode
On considère la suite v définie par v n =
u n−1
.
un +2
4. a) Prouver que v est une suite géométrique de raison
b) Calculer v0 et exprimer vn en fonction de n.
c) Exprimer un en fonction de vn, puis en fonction de n.
d) En déduire la convergence de la suite u et sa limite l.
2
.
5
Deux méthodes pour une suite
3 x+2
.
x+4
1. Étudier les variations de f et en déduire que, pour tout x élément de I, f (x) appartient à I.
10
2
On a f ' ( x)=
2 . Comme 10 et (x + 4) sont positifs, il en va de même pour f '(x).
( x+4)
1
Comme f (0) =
et f (1) = 1, on a le tableau de variation suivant :
2
I est l'intervalle [0,1]. On considère la fonction f définie sur I par f ( x)=
x
1
0
f '(x)
+
1
f (x)
1/2
1
 f (x)  1, donc f (x) appartient aussi à I.
2
2. On considère la suite u définie par u0 = 0 et un+1 = f (un). Montrer que pour tout entier naturel n, un
appartient à I.
Montrons que pour tout entier naturel n, un appartient à I par récurrence.
Initialisation : La propriété est vraie pour n = 0 car u0 = 0, donc u0 appartient à I.
Hérédité : Supposons que un appartient à I et montrons qu'alors un+1 appartient aussi à I.
Comme un appartient à I, la question 1 permet de dire que f (un) appartient aussi à I.
Or un+1 = f (un), on en déduit que un+1 appartient à I.
Conclusion : Ainsi, tout entier naturel n, un appartient à I.
On se propose d'étudier la suite u par deux méthodes différentes.
Première méthode
3. a) Représenter graphiquement f dans un repère orthonormal d'unité graphique 10 cm.
b) En utilisant le graphique précédent, placer les points A0, A1, A2 et A3 d'ordonnée nulle et
d'abscisses respectives u0, u1, u2 et u3.
Le tableau montre que si x appartient à I, on a
Que suggère le graphique concernant le sens de variation de u et sa convergence ?
La suite u semble être croissante et converger vers 1.
(1−un )(u n+2)
c) Établir la relation u n+1−u n=
et en déduire le sens de variation de la suite u.
u n+4
3 u n+2
−u 2n−un+2
, or (1−un )(u n+2)=−u 2n−un +2 , on a donc bien
u n+1−u n=
−u n=
u n+4
u n+4
(1−un )(u n+2)
u n+1−u n=
. Comme on sait que 0  un  1, 1 – un , un + 2 et un + 4 sont
u n+4
positifs, donc un+1 – un est positif et la suite u est croissante.
d) Démontrer que la suite u est convergente.
La suite u est croissante et majorée par 1, elle est donc convergente vers une limite l.
e) Prouver que la limite l de la suite u vérifie l = f (l) et calculer l.
Comme un+1 = f (un), on a lim un+1 = lim f (un). Or lim un+1 = lim un = l et lim f (un) = f (l) car f
3 l +2
est continue. Finalement on a bien l = f (l), soit l=
. Cette équation est équivalente à
l+4
l 2+l −2=0 qui a deux solutions l1 = 1 et l2 = -2. Comme les un sont tous positifs la limite l
ne peut pas être -2, donc l = 1.
Deuxième méthode
u n−1
On considère la suite v définie par v n =
.
un +2
2
4. a) Prouver que v est une suite géométrique de raison .
5
u n+1−1 2 u n−2 2 (u n−1) 2 un−1 2
v n+1 =
=
=
=
= v , donc v est bien une suite
un +1 +2 5 u n+10 5(un+2) 5 u n+2 5 n
2
géométrique de raison .
5
b) Calculer v0 et exprimer vn en fonction de n.
−1
2
1 2 n
v0 =
et v n =− ×
car la suite v est géométrique de raison .
2
2 5
5
c) Exprimer un en fonction de vn, puis en fonction de n.
u n−1
Comme v n =
, on a vnun + 2 vn = un – 1, donc un(vn – 1)= –1 – 2vn et finalement
un +2
−2 v n −1
u n=
v n −1
()
d) En déduire la convergence de la suite u et sa limite l.
2
2 n
Comme −1< <1 , lim
= 0 donc lim vn = 0.
5
5
−2 v n −1
−2×0−1
Comme u n=
, lim un =
=1.
v n −1
0−1
On retrouve bien le même résultat qu'avec la première méthode.
()