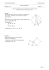n - Rosamaths

Ch 1 : Suites numériques ( 1ère partie )
Terminale S
Fiche d’objectifs du chapitre 1
SAVOIR
2015 - 2016
SAVOIR FAIRE
Rappels de 1ère S :
-
Savoir déterminer le sens de variations d’une suite
-
Savoir exploiter la représentation graphique d’une
suite pour conjecturer son sens de variations .
Représentation graphique
-
Savoir représenter graphiquement une suite
définie par récurrence .
Suites arithmétiques
-
Savoir démontrer qu’une suite est arithmétique ou
non .
Déterminer la forme explicite de un en fonction
de n .
Utiliser une suite auxiliaire arithmétique ( vn )
pour déterminer la forme explicite d’une suite
quelconque ( un ) .
Savoir calculer une somme de termes consécutifs
d’un e suite arithmétique .
Sens de variation d’une suite
-
-
Suites géométriques
-
-
Savoir démontrer qu’une suite est géométrique
ou non .
Déterminer la forme explicite de un en fonction
de n .
Utiliser une suite auxiliaire géométrique ( vn )
pour déterminer la forme explicite d’une suite
quelconque ( un ) .
Savoir calculer une somme de termes consécutifs
d’une suite géométrique .
Suites bornées
-
Savoir démontrer qu’une suite est majorée ou
minorée ou bornée .
Raisonnement par récurrence
-
Savoir mener un raisonnement par récurrence .
TICE
-
Savoir calculer avec une calculatrice les premiers
termes d’une suite ou un terme de rang donné .
-
Savoir comprendre , modifier ou compléter un
algorithme .
1
Exercices
I – Rappels de première S :
I . 1 Définition d’une suite :
• Suite définie par une formule :
Exemples :
∀n ∈ ℕ , un = f ( n )
1) Calculer les cinq premiers termes de la suite
(u )
2) Calculer les cinq premiers termes de la suite
( u ) définie sur
n
n∈ℕ
définie par un =
n
ℕ * par un = n − 1 .
Remarques : 1) On dit que : a) la suite ( un ) est définie de façon explicite
b) un est exprimé en fonction de n
2) La suite ( un ) n'est pas forcément définie à partir du rang n = 0 .
2
n +1
.
n+2
• Suite définie par son premier terme et une relation de récurrence :
Exemples :
1) On considère la suite
( un )n∈ℕ définie par :
u0 = a
u = f ( u )
n
 n +1
u0 = 0

u = un + 1
 n +1 un + 2
Calculer u1 , u2 et u3
2) On considère la suite
(u )
n
n∈ℕ *
définie par :
{uu ==0 2u + n
1
n +1
Calculer les quatre premiers termes de la suite .
Remarques : 1) On dit que : a) la suite ( un ) est définie par récurrence
b) un +1 est exprimé en fonction de un
2) Le terme initial de la suite ( un ) n'est pas forcément u0 .
3
n
I . 2 Etude du sens de variation d’une suite :
• Etude du signe de un +1 − un :
Si ∀n ∈ ℕ , un +1 − un ≥ 0 , alors la suite ( un ) est croissante
Si ∀n ∈ ℕ , un +1 − un ≤ 0 , alors la suite ( un ) est décroissante
Exemples :
1) Montrer que la suite ( un ) n∈ℕ définie par un =
n +1
est croissante .
n+2
2) Montrer que la suite ( un ) n∈ℕ définie par un = − n 2 + 5n − 6 est décroissante à partir du rang 3.
Remarques : 1) Si le signe de un +1 − un n'est pas constant , alors la suite n'est pas monotone .
2) Une suite ( un ) peut n'être monotone qu'à partir d'un certain rang .
4
• Cas d’une suite définie de façon explicite :
Si ∀n ∈ ℕ , un = f ( n ) , on peut étudier les variations de f sur ℝ + :
1) Si f est croissante sur ℝ + alors la suite ( un ) est croissante
2) Si f est décroissante sur ℝ + alors la suite ( un ) est décroissante
Exemple : En utilisant les variations de la fonction associée , montrer que la suite ( un ) n∈ℕ définie par
un =
n +1
est croissante .
n+2
Remarque : Cette propriété n'est pas vraie si la suite est définie par récurrence .
Contre - exemple :
{uu ==2−2u + 3
0
n +1
n
On a un +1 = f ( un ) avec f ( x ) = −2 x + 3 .
La fonction f est décroissante sur ℝ mais la suite ( un ) n'est pas monotone ( vérifier à la calculatrice ) .
5
I . 4 Différents outils pour faire des conjectures sur une suite :
•
Calculatrice graphique :
Avec une TI :
Avec une Casio :
Exemple : On considère la suite définie par
u0 = 0

un +1 = 2un − n
A l'aide de la calculatrice :
1) calculer les dix premiers termes de cette suite
2) conjecturer le sens de variations de cette suite
6
•
Représentation graphique :
Exemple : On considère la suite ( un ) n∈ℕ* définie par
u1 = 2

un +1 = −2un + 3
On a tracé ci - dessous les droites d'équation respective y = x et y = −2 x + 3 .
Sans les calculer , représenter graphiquement les 4 premiers termes de la suite
7
(u ) .
n
•
Algorithmes :
Exemple 1 : On considère la suite ( un )n∈ℕ définie par
u0 = −2

un +1 = un + 3
On considère l’algorithme suivant :
Variables :
n et i sont des entiers naturels
u est un réel
Initialisation :
Saisir la valeur de N
Affecter à u la valeur −2
Traitement et sortie : Pour i allant de 1 à N
Afficher u
Affecter à u la valeur
u+3
Fin Pour
1) Compléter le tableau suivant pour N = 4 :
Valeur de i
Affichage
Valeur de u
Etape initiale
Etape 1
Etape 2
Etape 3
Etape 4
2) Que fait cet algorithme ?
3) Modifier cet algorithme pour qu’il affiche seulement le ( n + 1)
8
ième
terme de la suite.
Exemple 2 : On considère la suite ( un )n∈ℕ définie par
u0 = 0

un +1 = 2un − n
On considère l’algorithme suivant :
Variables :
n est un entier naturel
u est un réel
Initialisation : Saisir la valeur de N
Affecter à n la valeur 0
Affecter à u la valeur −1
Traitement : Tant que n < N
Affecter à u la valeur 2u − n
Affecter à n la valeur n + 1
Fin Tant que
Sortie :
Afficher u
1) Que fait cet algorithme ?
2) Modifier cet algorithme pour qu’il calcule et affiche tous les termes de la suite de u1 à u N .
9
I . 4 Suites arithmétiques :
•
Définition par récurrence :
Une suite
(u )
n
n∈ℕ
est arithmétique lorsque chaque terme se
déduit du précédent en lui ajoutant une constante r appelée raison de la suite :
s’il existe un réel r tel que , pour tout n ∈ ℕ , un +1 = un + r .
•
Méthodes :
1) Pour démontrer qu’une suite est arithmétique , il faut montrer que un +1 − un est un
nombre constant ( indépendant de n ) . Cette constante est alors la raison de la suite.
Exemple : Démontrer que la suite définie par ∀n ∈ ℕ , un = 3n − 5 est arithmétique .
2) Pour démontrer qu’une suite n’est pas arithmétique , il faut démontrer que la différence entre
deux termes consécutifs n’est pas constante .
Exemple : Démontrer que la suite définie par ∀n ∈ ℕ , un = n 2 + 1 n'est pas arithmétique .
10
•
Formule explicite de un en fonction de n :
Soient n et p deux entiers naturels tels que p ≤ n .
(u )
n
est la suite arithmétique définie à partir du rang p et de raison r
si et seulement si on a :
un = u p + ( n − p ) r
Remarques : 1) Si le premier terme de la suite est u0 , alors ∀n ∈ ℕ un = u0 + nr
2) Si le premier terme de la suite est u1 , alors ∀n ∈ ℕ un = u1 + ( n − 1) r
•
Somme de termes consécutifs :
On considère une suite arithmétique ( un ) de raison r définie à partir d’un certain rang p , p ∈ ℕ .
Alors la somme des termes consécutifs de la suite de u p à un est :
n
∑u
i
= u p + u p +1 + ... + un −1 + un = ( n − p + 1) ×
u p + un
2
i= p
.
Remarque : On peut retenir que S = nombre de termes ×
Cas particulier :
1er terme + dernier terme
2
n
n ( n + 1)
i =0
2
∑ i = 0 + 1 + 2 + ... + ( n − 1) + n =
I . 5 Suites géométriques :
•
Définition par récurrence : Une suite
(u )
n
n∈ℕ
est géométrique lorsque chaque terme se déduit du
précédent en le multipliant par une constante q appelée raison de la suite : s’il existe un réel q tel
que , pour tout n ∈ ℕ , un +1 = un × q .
•
Méthodes :
1) Pour démontrer qu’une suite est géométrique, il faut démontrer que ∀n ∈ ℕ , un +1 = un × q
Exemple : Démontrer que la suite définie par ∀n ∈ ℕ , un = 3n est géométrique .
11
2) Pour démontrer qu’une suite n’est pas géométrique, il suffit de trouver deux indices p et q
tels que les quotients
u p +1
up
et
u q +1
uq
ne soient pas égaux.
Exemple : Démontrer que la suite définie par ∀n ∈ ℕ , un = n + 1 n'est pas géométrique .
•
Formule explicite de un en fonction de n :
Soient n et p deux entiers naturels tels que p ≤ n .
(u )
n
est la suite géométrique définie à partir du rang p et de raison q
si et seulement si on a : un = u p × q n − p
Remarques : 1) Si le premier terme de la suite est u0 , alors ∀n ∈ ℕ un = u0 × q n
2) Si le premier terme de la suite est u1 , alors ∀n ∈ ℕ un = u1 × q n −1
•
Somme de termes consécutifs :
On considère une suite géométrique ( un ) de raison q définie à partir d’un certain rang p , p ∈ ℕ .
Alors la somme des termes consécutifs de la suite de u p à un est :
1 − q n − p +1
.
ui = u p + u p +1 + ... + un −1 + un = u p ×
∑
1− q
i= p
n
1 − raison nombre de termes
Remarque : On peut retenir que S = 1er terme ×
1 − raison
n
Cas particulier :
∑ qi = 1 + q + q 2 + ... + q n −1 =
i =0
12
1 − q n +1
1− q
II – Suites majorées , minorées , bornées :
Définitions : On considère deux réels m et M . La suite ( un ) est dite :
•
majorée par M si ∀n ∈ ℕ , un ≤ M
•
minorée par m si ∀n ∈ ℕ , un ≥ m
•
bornée par m et M si ∀n ∈ ℕ , m ≤ un ≤ M
Exemple : On considère la suite ( un ) définie sur ℕ∗ par un = 1 +
Démontrer qu'elle est bornée par 1 et 3 .
13
2
.
n
Remarques :
1) On dit que m est un minorant de la suite
(u ) .
n
Si m est un minorant de la suite ( un ) , alors tout nombre k tel que k ≤ m est aussi un minorant
de la suite ( un ) . Dans ce cas , la suite ( un ) a une infinité de minorants .
2) On dit que M est un majorant de la suite
(u ) .
n
Si M est un majorant de la suite ( un ) , alors tout nombre K tel que M ≤ K est aussi un
majorant de la suite ( un ) . Dans ce cas , la suite
(u )
n
a une infinité de majorants .
3) Il existe des suites non minorées , non majorées . Par exemple , la suite ( un ) définie sur ℕ par
n
un = ( −2 ) n’est ni minorée , ni majorée .
Théorème :
•
Toute suite croissante est minorée par son premier terme .
•
Toute suite décroissante est majorée par son premier terme .
14
III – Le raisonnement par récurrence :
Exemple : On considère la suite ( un )n∈ℕ définie par
u0 = −2

un +1 = un + 3
A l'aide de la calculatrice :
1) calculer les vingt premiers termes de cette suite
2) conjecturer le plus petit entier naturel N tel que , ∀n ∈ ℕ , un < N
Axiome de récurrence :
On considère une propriété ( Pn ) dépendant d’un entier naturel n .
Pour démontrer que la propriété
(P )
n
est vraie pour tout entier naturel n , il suffit de démontrer :
• que la proposition est vraie au rang 0 .
Cette étape est appelée l’initialisation : on vérifie que «
(P )
0
est vraie »
• que la propiété est héréditaire :
On suppose que la propriété ( Pk ) est vraie pour un certain entier naturel k quelconque .
C’est l’hypothèse de récurrence .
On démontre alors que la propriété ( Pk +1 ) est vraie .
Remarque : On peut démontrer de façon analogue qu'une propriété ( Pn ) ∀n ∈ ℕ , n ≥ n0 :
il suffit de vérifier l'initialisation au rang n0 .
Remarque : Ne pas confondre suite définie par récurrence et démonstration par récurrence .
15
Exemple : On considère la suite ( un ) n∈ℕ définie par
u0 = −2

un +1 = un + 3
Démontrer par récurrence que , ∀n ∈ ℕ , − 3 < un < 3
Rédaction - type :
16