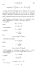MESURE DE L`INFORMATION

MESURE DE L'INFORMATION
Marc URO
TABLE DES MATIÈRES
INTRODUCTION............................................................................................................... 3
INCERTITUDE D'UN ÉVÉNEMENT (OU SELF-INFORMATION).................... 7
INFORMATION MUTUELLE DE DEUX ÉVÉNEMENTS .................................. 9
ENTROPIE D'UNE VARIABLE ALÉATOIRE DISCRÈTE .................................. 10
ENTROPIE ET INFORMATION LIÉES À UN COUPLE DE
VARIABLES............................................................................................................. 13
INFORMATION MUTUELLE CONDITIONNELLE............................................ 16
3
INTRODUCTION
Les premières tentatives de définition de mesure de l'information datent des années
vingt. Citons Nyquist pour l'aspect communication et Fisher d'un point de vue
statistique (l'information de Fisher figure dans la borne de Cramer-Rao qui est un
minorant de la variance d'une certaine classe d'estimateurs). Mais ce n'est qu'à partir de
1948, grâce aux travaux de Shannon, que la théorie de l'information a pris sa forme
actuelle.
Donner une définition précise et complète de la théorie de l'information est une tâche
difficile. Pour simplifier on peut énoncer l'assertion suivante; La théorie de
l'information est une discipline fondamentale qui s'applique dans le domaine des
communications. Son objet consiste d'une part à déterminer les limites imposées par les
lois de la nature lorsqu'on doit stocker ou transmettre le contenu d'une source
(d'information), d'autre part à proposer des dispositifs permettant d'atteindre ou
d'approcher ces limites. La théorie de l'information ne cesse de se développer car les
exigences actuelles s'orientent vers une augmentation constante de l'information à
stocker ou à transmettre.
Exemple: Norme 4.2.2 de la télévision numérique (adoptée en 1981 par le CCIR,
Comité Consultatif International des Radiocommunications)
Cas d'une image couleur fixe
Une image est caractérisée par trois composantes Y, Cb, Cr que l'on appelle les
primaires. Y est la caractéristique de luminance tandis que Cb et Cr sont des
caractéristiques de chrominance. L'image est formée de points (ou pixels) qui sont au
nombre de 720 pour chacune des 576 lignes. Chaque primaire est codée sur 8 éléments
binaires correspondant à 2 8 = 256 niveaux de quantification. D'autre part, l'oeil étant
moins sensible à la couleur qu'à la luminance, on estime qu'il est suffisant que les
primaires Cb et Cr ne soient présentes qu'un point sur deux.
Ainsi on peut calculer le nombre d'éléments binaires contenus dans une image:
6,63
576 × 720 × 8 + (576 × 360 × 8) × 2 ≈ 6,63 × 10 6 eb soit
≈ 0,83 Moctet .
8
4___________________________________________________________ introduction
La capacité d' une disquette 3 pouces 1/2 haute densité étant d'environ 1,4 Moctet
après formatage, on constate qu'une telle disquette ne peut contenir qu'une seule
image.
Cas d'une image couleur animée
La fréquence image est de 25 Hertz (25 images par seconde). Ainsi la transmission
d'une séquence animée nécessite un débit net de:
6
6,63 × 10 × 25 ≈ 166 Mbits / sec .
En fait ce débit ne tient pas compte des signaux complémentaires indispensables à la
synchronisation. En ajoutant ces signaux dits signaux de service, on obtient un débit
brut de 216 Mbits / sec .
Sachant que sur le réseau numérique, le débit maximum est de 144 Mbits / sec , on
constate que la transmission d'un tel signal nécessitera des traitements.
Le traitement du contenu d'une source d'information peut être envisagé sous deux
formes:
- sans perte d'information,
- avec perte d'information.
Nous nous limiterons, dans le cadre de ce fascicule, au traitement sans perte (ou
presque) d'information.
Le schéma d'une communication peut être représenté comme suit: (il s'agit du
paradigme de Shannon)
SOURCE
codage de source
codage de canal
C
A
N
A
L
mots source restitués
décodage de source
décodage de canal
introduction ___________________________________________________________ 5
Le codage de source consiste à éliminer les redondances de la source afin d'en réduire le
débit binaire.
Le codage de canal a un rôle de protection contre les erreurs (dues à la transmission sur
le canal) qui est assuré en ajoutant de la redondance (codes correcteurs d'erreurs).
Les points de vue codage de source et codage de canal sont donc fondamentalement
différents.
Le plan du fascicule est organisé comme suit:
CHAPITRE I
Définitions des grandeurs informationnelles concernant les événements et les variables
aléatoires.
CHAPITRE II
Extension de la notion d' entropie (incertitude moyenne) d'une variable aléatoire à la
notion d'entropie d'une source discrète. Étude du problème posé par le codage de
source.
CHAPITRE III
Caractérisation et modélisation des supports de transmission du point de vue de leur
aptitude à transmettre de l'information. Capacité d'un canal discret, codage de canal.
CHAPITRE IV
Aptitude des codes linéaires à détecter et corriger des erreurs.
7
MESURE DE L'INFORMATION
INCERTITUDE D'UN ÉVÉNEMENT (OU SELF-INFORMATION)
La difficulté rencontrée pour définir la self-information relative à un événement est liée
au caractère subjectif de l'information effectivement apportée par la réalisation de cet
événement.
Pour gommer cet aspect subjectif, on peut considérer qu'a postériori la quantité
d'information reçue est d'autant plus grande que l'on ne s'attendait pas à observer la
réalisation d'un événement. En d'autres termes on peut aussi énoncer qu'a priori,
l'incertitude d'un événement est d'autant plus grande que l'on ne s'attend pas à ce qu'il se
réalise.
Prenant en compte la correspondance entre l'incertitude (ou self-information) d'un
événement et son caractère plus ou moins probable, on est amené à définir la mesure
d'incertitude (ou self-information) comme une fonction d'une application probabilité.
Ceci nécessite de disposer d'un espace probabilisé.
Soient (Ω, T, P) un espace probabilisé et E un événement de T. On se propose de définir
une mesure d'incertitude h(E) liée à l'événement E de telle sorte que:
 1 

- h(E) soit d'autant plus grande que P{E} est petite. On peut poser h( E ) = f 
 P {E}
avec f fonction croissante.
- h( E ) = 0 si P{E} = 1. Il n'y a aucune incertitude quant à la réalisation d'un
événement certain. Donc f (1) = 0.
- Si E et F sont deux événements indépendants, h( E ∩ F ) = h(E ) + h( F ) c'est-à-dire:

 1
 1 

1
1 
+
= f
×
= f
f
 P{E ∩ F }
 P {E } P{F}
 P{E}
On recherche donc une fonction f telle que:
 1 
.
f
 P{F }
8__________________________________________________ mesure de l'information
 f : [1,+∞ [ → IR+
 f est croissante

f (xy) = f ( x ) + f (y )

î f (1) = 0
On va établir une équation différentielle vérifiée par f .
En dérivant les deux membres de l'équation f (xy) = f ( x ) + f (y ) par rapport à x, on
obtient : y f ' (xy ) = f ' (x ) ∀ x,y .
1 1
Soit, en prenant y = , f ' (1) = f ' (x ) .
x x
On a donc f ′( x ) =
1
f ′(1) avec
x
f ′(1) > 0
La solution est de la forme: f ( x ) = α Ln x avec α > 0 soit encore:
f (x ) = β
Ln x
Ln a
avec β > 0 et
a > 1. On peut choisir β = 1.
Si on prend a = e , f est la fonction logarithme népérien et l'unité d'incertitude est le
nat. Si on choisit a = 2 , f est la fonction logarithme à base deux et l'unité d'incertitude
est le bit ou le Shannon.). On notera désormais log le logarithme à base a.
Remarque : Ici bit est l'abréviation de binary unit qu'il ne faut pas confondre avec binary
digit.
On a donc h( E ) = −log P{E}
(1) et h(E ) peut être interprété:
- a priori, par l'incertitude qui règne sur la réalisation de E.
- a postériori, par l'information apportée par la réalisation de E.
On peut bien sûr étendre la définition de h( E ) au cas d'une application probabilité
conditionnelle et on note alors: h( F / E ) = − log P{F / E }. Remarquant que
P{E ∩ F} = P{E} × P {F / E}, on déduit:
h( E ∩ F ) = h( E ) + h(F / E ) ∀( E, F ) ∈ T2
(2 ) .
mesure de l'information__________________________________________________ 9
Dans le cas particulier où E et F sont indépendants, on retrouve l'axiome:
h( E ∩ F ) = h( E ) + h( F )
(2′ ) .
INFORMATION MUTUELLE DE DEUX ÉVÉNEMENTS
L'information apportée par F sur E est la diminution de l'incertitude sur E lorsque F
est réalisé.
IF → E = h( E ) − h( E / F)
(3)
IF → E = − log P{E} + log P {E / F} = − log P{E} + log
IF → E = log
P {E ∩ F }
P {F}
P{E ∩ F }
P{E} × P {F / E }
= log
= − log P{F} + log P {F / E}
P{E }× P{F }
P{E} × P{F}
IF → E = h( F ) − h(F / E) = I E →F
(3′)
Comme IE → F = IF→ E , on appelle information mutuelle entre E et F la quantité:
I( E;F ) = I E→ F = IF → E .
Si E et F sont indépendants, alors P{F / E} = P{F } et
I (E; F ) = 0 .
En combinant (2) et (3'), on obtient: h( E ∩ F ) = h( E ) + h( F ) − I (E; F )
On peut résumer les relations précédentes sur un diagramme de Venn:
h(F)
h(E)
I(E;F)
(4)
10_________________________________________________ mesure de l'information
.
ENTROPIE D'UNE VARIABLE ALÉATOIRE DISCRÈTE
Soit X une variable aléatoire à valeurs dans
n = +∞ ) telle que pi = P {X = x i} ∀ i ∈[1, n] .
{x1 , x2 ,..., x n }
(avec éventuellement
L'entropie de X notée H(X) est la moyenne des incertitudes calculée sur les événements
{X = x i }.
n
H(X ) = − ∑ pi log pi
(5)
i=1
Remarques
- H(X) dépend de la loi de probabilité de X mais n'est pas fonction des valeurs prises
par X.
- H(X) correspond à l'espérance mathématique de la variable aléatoire incertitude IX
définie par IX = − log P(X ) avec P( X ) = pi sur {X = x i }. On a donc :
n
IX = − ∑1I{X =x i } log pi . Soit H(X ) = E[I X ]= E [− log P( X )].
i=1
- Exprimée en Shannons, H(X) représente le nombre moyen de bits nécessaires à la
codification binaire des différentes réalisations de X.
Exemple
On extrait au hasard une carte d'un jeu de 32 cartes. A chacune des 32 cartes on associe
une valeur différente des 31 autres valeurs correspondant aux 31 autres cartes par le
biais d'une variable aléatoire X. Les valeurs prises par X ne sont pas précisées car elles
n'interviennent pas dans le calcul de H(X). De plus on suppose que chaque carte a la
même probabilité d'être extraite.
On a H(X ) = −32 ×
1
1
× log2
= log 2 32 = 5 Sh .
32
32
mesure de l'information_________________________________________________ 11
Pour savoir quelle carte a été extraite, on peut demander si sa couleur est rouge ou
noire, s'il s'agit d'un coeur ou d'un carreau (resp un trèfle ou un pique), si la carte
appartient au groupe (7, 8, 9, 10) ou (valet, dame, roi, as), puis à quel sous-groupe
constitué de deux cartes elle appartient et enfin laquelle des deux cartes correspond à la
carte tirée. Les réponses à ces cinq questions peuvent être résumées par cinq bits ('1'
pour oui et '0' pour non).
Une autre façon de modéliser le problème consiste à attribuer un numéro (de 0 à 31) à
chaque carte. L'écriture de ces numéros en base deux requiert log 2 32 = log2 2 5 = 5 bits
PROPRIÉTÉS DE L'ENTROPIE
Lemme
Soient (p1 , p2 ,..., pn ) et (q1 ,q2 ,...,qn ) deux lois de probabilité, alors:
En effet ∀x > 0 on a
Ln x ≤ x − 1
x-1
Ln x
0
D'où Ln
1
qi qi
q
1  qi 
−1
≤ − 1, soit log i ≤
pi Ln a  pi 
pi pi
x
n
qi
∑ p log p
i =1
i
i
≤0.
12_________________________________________________ mesure de l'information
n
donc
∑ pi log
i =1
n

qi
1 n  qi
1  n
1

≤
−
=
−
(1 − 1) = 0
p
q
pi =
1
∑
∑
∑
i
i
 Ln a
 Ln a  i =1
pi Ln a i =1  pi
i =1
Propriété 1
L'entropie d'une variable aléatoire X à n valeurs possibles est maximum et vaut log(n)
lorsque la loi de X est uniforme.
Il suffit d'appliquer le lemme précédent avec q1 = q2 =... = qn =
n
n
i =1
i=1
Ainsi, − ∑ pi log pi ≤ − ∑ pi log
1
.
n
n
1
1
1
= − ∑ log = − log n.
n
n
i=1 n
L'incertitude sur X est la plus grande si toutes les valeurs possibles ont la même
probabilité de se réaliser.
Propriété 2
L'entropie augmente lorsque le nombre de valeurs possibles augmente.
En effet soit X à valeurs possibles {x1 , x2 ,..., x n } de loi (p1 , p2 ,..., pn ). Supposons que la
valeur xk de probabilité pk soit 'éclatée' en deux valeurs yk et zk de probabilités α k , β k
avec α k + β k = pk α k ≠ 0 et β k ≠ 0 . Alors l'entropie de la nouvelle variable aléatoire
X' ainsi obtenue s'écrit H(X ′ ) = H( X ) + pk log pk − α k log α k − β k log β k . d'où
H(X ′ ) − H(X ) = (α k + β k )log pk − α k log α k − β k log β k
H(X' ) − H( X ) = α k log pk + β k log pk − α k log α k − β k log β k .
Or, la fonction logarithme étant strictement croissante, on a:
log pk > log α k et log pk > log β k soit H(X ′ ) − H(X ) > 0 , c'est-à-dire:
H(X ′ ) > H ( X ) .
Propriété 3
L'entropie est une fonction ∩ convexe de (p1 , p2 ,..., pn ).
n
n
i=1
i =1
En effet H(X ) = − ∑ pi log pi = ∑ gofi ( p1 , p2 ,..., pn )
mesure de l'information_________________________________________________ 13
avec f i l'application projection sur l'axe i:
f i : [0,1] → [0,1]
n
et
(p1 , p2 ,..., pn ) → pi
g: [0,1]→ IR +
p → − plog p
1 p
1
1
=−
− log p et g ′′( p) = − < 0 .
Ln 2 p
Ln 2
p
Comme f i est une forme linéaire, gof i est ∩ convexe et H(X) est ∩ convexe car
g est ∩ convexe car g ′(p ) = − log p −
somme de fonctions ∩ convexes.
ENTROPIE ET INFORMATION LIÉES À UN COUPLE DE
VARIABLES
Soient X et Y deux variables aléatoires discrètes respectivement à valeurs dans
{x1 , x2 ,..., x n } et {y1 , y2 ,...,y m }. Si on désigne par pij = P {X = x i ∩ Y = y j } la loi du
couple (X, Y), on peut sans difficulté prolonger la définition de l'entropie d'une variable
aléatoire à l'entropie d'un couple de variables aléatoires. Ainsi:
n
m
H(X,Y ) = − ∑ ∑ pij logpij
(6)
i =1 j =1
On peut également, en s'inspirant des grandeurs informationnelles relatives aux
événements, définir les entropies conditionnelles et l'information mutuelle:
H(X / Y = y j ) = − ∑ P{X = xi / Y = y j }log P {X = x i / Y = y j }
n
(7)
i =1
Par la suite, on notera pi / j = P{X = xi / Y = y j }.
H(X / Y ) = ∑ P{Y = y j }H (X / Y = y j )
m
j =1
H(X / Y ) = − ∑ ∑ P{Y = y j }P {X = x i / Y = y j }log P{X = x i / Y = y j }
m
n
j =1 i=1
14_________________________________________________ mesure de l'information
n
m
soit H(X / Y ) = − ∑ ∑ pij log pi / j
(8)
i =1 j =1
H(X / Y ) représente l'incertitude sur X lorsqu'on connait Y.
De même l'information mutuelle moyenne entre X et Y peut s'écrire:
I( X;Y ) = H (X) − H (X / Y ) = H(Y) − H (Y / X)
(9)
I(X;Y) correspond à la diminution de l'incertitude sur X (resp. Y) lorsqu'on connait Y
(resp. X).
D'après (9), on a:
n
m
n
I( X;Y ) = − ∑ pi log pi + ∑ ∑ pij log pi/ j
i =1
(10)
j =1 i =1
m
or pi = ∑ pij donc
j =1
n
m
n
m
I(X;Y ) = − ∑ ∑ pij log pi + ∑ ∑ pij log pi/ j d'où
i =1 j =1
n
i =1 j =1
m
I(X;Y ) = ∑ ∑ pij log
i=1 j =1
n
m
pi / j
p
= ∑ ∑ pij log ij
pi
pi p. j
i =1 j =1
P(X,Y ) 

On a donc I(X;Y ) = E log
P(X )P(Y ) 

n
(11) avec p. j = ∑ pij `
i =1
(12)
Propriétés
- L'information mutuelle moyenne de X et de Y est toujours positive (ce n'est pas le
cas pour l'information mutuelle entre deux événements qui prend des valeurs négatives
lorsque la réalisation de l'un des événements rend l'autre moins probable).
n
m
On a − I(X;Y ) = ∑ ∑ pij log
i =1 j =1
pi p. j

1 n m  pi p. j
pij 
≤
− 1 car Ln x ≤ x − 1
∑
∑
pij
Ln 2 i=1 j =1  pij

mesure de l'information_________________________________________________ 15
d'où − I(X;Y ) ≤
n m

1  n m
1
 ∑ ∑ pi p. j − ∑ ∑ pij  =
(1 − 1) = 0
Ln 2  i =1 j =1
 Ln 2
i=1 j =1
- Le conditionnement diminue l'incertitude
En d'autres termes cela signifie que H(X ) ≥ H( X / Y ) . Il suffit d'appliquer (9) en
utilisant la propriété précédente.
- H(X ) + H(Y ) = H (X,Y ) + I(X;Y )
n
m
(14 )
n
n
m
En effet H(X ) = − ∑ pi log pi = − ∑ ∑ p j /i pi log pi = − ∑ ∑ pij log pi
i =1
j =1 i = 1
n
n
i = 1 j=1
m
De même H(Y ) = − ∑ p. j log p. j = − ∑ ∑ pij log p. j
i =1 j =1
i=1
n
m
n
m
n
m
On a donc H(X ) + H(Y ) = − ∑ ∑ pij log pi p. j = − ∑ ∑ pij log pij + ∑ ∑ pij log
i=1 j =1
i =1 j =1
i =1 j =1
D'où H(X ) + H(Y ) = H(X,Y ) + I(X;Y)
- H(X,Y ) = H (X) + H (Y / X) = H(Y ) + H(X / Y )
(15)
Ce résultat s'obtient facilement en combinant (9) et (14).
On peut illustrer ces relations par une représentation en diagramme de Venn:
H(X)
H(Y)
H(X/Y)
I(X;Y) H(Y/X)
pij
pi p. j
16_________________________________________________ mesure de l'information
Dans le cas particulier où X et Y sont indépendantes, en reprenant (7), (8), (9) et (14),
on obtient:
H(X / Y = y) = H (X)
H(X / Y ) = H(X )
(16)
I(X;Y ) = 0
(17)
H(X ) + H(Y ) = H (X,Y )
(18)
INFORMATION MUTUELLE CONDITIONNELLE
Par extension de la formule (9), on peut introduire la notion d'information mutuelle
(moyenne) entre deux variables X et Y conditionnellement à l'événement {Z = z } où Z
est une troisième variable:
I(X;Y / Z = z ) = H(X / Z = z ) − H(X / Y , Z = z)
(19)
En multipliant les deux membres de (19) par P{Z = z } et en sommant sur toutes les
valeurs possibles de Z, on obtient:
∑ P{Z = z}I(X;Y / Z = z ) = H(X / Z) − H( X / Y , Z)
z
Le membre de gauche pouvant être interprété comme I( X; Y / Z ) , on définit
l'information mutuelle entre X et Y sachant Z par
I(X;Y / Z ) = H( X / Z ) − H( X / Y, Z ) = H(Y / Z) − H (Y / X,Z )
(20)
Nous allons maintenant montrer que:
I(X;(Y, Z )) = I(X;Y ) + I(X;Z / Y )
(21)
En appliquant (9) au couple (X, (Y, Z )) , on obtient
I(X;(Y , Z)) = H (X) − H(X / Y ,Z ) , mais I(X;Z ) = H(X) − H (X / Z ) , soit:
H(X ) = I(X; Z) + H(X,Z ) d'où:
I ( X ;(Y , Z )) = I ( X ; Z ) + H ( X / Z ) − H( X / Y , Z ). D'où en appliquant (20):
I ( X ;(Y , Z )) = I ( X ; Z) + I ( X ; Y / Z )
mesure de l'information_________________________________________________ 17
Notons que si Y est indépendante de X sachant Z, ie P{Y / X,Z} = P{Y / Z }, on a:
H(Y / X,Z ) = H(Y / Z ) et ainsi I(X;Y / Z) = 0.
Les relations énoncées ci-dessus vont nous permettre d'établir une propriété importante
vérifiée par l'information mutuelle qui nous permettra de définir la capacité d'un canal.
Si on note p = (p1 , p2 ,..., pn ) le vecteur représentant la loi de probabilité de X et Q celui
correspondant aux probabilités conditionnelles p j / i = P{Y = y j / X = x i}, on peut alors
considérer I ( X ;Y ) comme une fonction des deux variables p et Q que l'on note I ( p; Q).
Nous allons montrer que:
I( p;Q) est une fonction ∩ convexe de p et ∪ convexe de Q.
- Montrons tout d'abord que I(p;Q) est une fonction ∩ convexe de p. Pour cela on se
fixe le vecteur de probabilités de transition Q et on se donne p0 et p1 deux vecteurs de
probabilité pour X. Il nous faut montrer que ∀ θ ∈[0,1] , on a:
θ I( p0 ;Q) + (1− θ )I(p1 ;Q) ≤ I(p;Q) où p = θ p0 + (1− θ )p1 .
L'idée consiste à interpréter p0 et p1 comme des probabilités conditionnellement à une
variable auxiliaire Z pouvant prendre les valeurs 0 et 1 avec les probabilités respectives
θ et 1 − θ .
Ainsi la iième composante de p0 peut s'écrire: p0 (i) = P{X = x i / Z = 0}.
De même la iième composante de p1 peut s'écrire: p1 (i) = P{X = x i / Z = 1}.
Le vecteur p représente la loi de X puisque:
θ p0 (i) + (1 − θ ) p1 (i) = P{Z = 0}P{X = xi / Z = 0} + P{Z = 1}P{X = xi / Z = 1}
θ p0 (i) + (1 − θ ) p1 (i) = P{X = xi ∩ Z = 0} + P{X = xi ∩ Z = 1} = P{X = x i }= pi (car les
événements {Z = 0} et {Z = 1} sont complémentaires).
De plus, on peut imposer l'indépendance entre les deux variables Y et Z sachant X (ie
P{Y / Z , X} = P{Y / X}), de telle sorte que I(p0 ;Q) (resp. I(p1 ;Q)) puisse être
interprété comme I(X;Y / Z = 0) (resp. I(X;Y / Z = 1)).
18_________________________________________________ mesure de l'information
Ainsi le membre de gauche de l'inégalité s'écrit:
P{Z = 0}I(X;Y / Z = 0) + P{Z = 1}I(X;Y / Z = 1) = I(X;Y / Z ) .
On est donc conduit à montrer que: I(X;Y / Z) ≤ I(X;Y ) .
Or I(Y; X,Z ) = I(Y; X ) + I(Y ; Z / X) ⇔ (1) , soit en permutant les rôles de X et Z:
I(Y; X,Z ) = I(Y; Z ) + I(Y; X / Z ) ⇔ (2) .
Or P{Y / Z , X} = P{Y / X)} ⇒
H(Y / Z, X ) = H(Y / X )
d'où I(Y; Z / X) = H(Y / X) − H (Y / Z, X) = 0.
(1) ⇒ I(Y ;( X, Z )) = I(Y; X) = I(X;Y ) et
(2) ⇒
I(Y; X / Z ) = I(Y ;(X,Z )) − I(Y, Z) ≤ I(Y;(X, Z)) = I(X;Y ) (cqfd).
- Montrons maintenant que I(p;Q) est une fonction ∪ convexe de Q à p fixé.
Soient Q0 et Q1 deux probabilités de transition et θ ∈[ 0,1] . Si on pose
Q = θ Q0 + (1 − θ )Q1 , il faut montrer que θ I( p;Q0 ) + (1 − θ )I(p;Q1 ) ≥ I(p;Q) . On peut de
plus considérer Q0 et Q1 comme des lois condiditionnelles à une variable binaire
auxiliaire Z indépendante de X et telle que:
Q0 ( j / i) = P{Y = y j / X = xi ∩ Z = 0}
Q1 (j / i) = P{Y = y j / X = xi ∩ Z = 1}
θ = P {Z = 0}
1 − θ = P{Z = 1}
Ainsi le membre de gauche de l'inégalité à montrer devient:
P{Z = 0}I(X;Y / Z = 0) + P{Z = 1}I(X;Y / Z = 1) = I(X;Y / Z ) .
On doit donc établir que I(X;Y / Z) ≥ I(X;Y ) . Pour cela on utilise:
I(X;(Y , Z)) = I(X;Y ) + I( X; Z / Y ) = I(X;Z ) + I(X;Y / Z) . Et l'indépendance de X et Z
entraîne I(X;Z ) = 0 .
D'où I(X;Y / Z) = I(X;(Y, Z )) = I(X;Y ) + I(X;Z / Y) ≥ I(X;Y ) (cqfd).