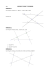cours théorème de thalès

3ème
Cours : Théorème de Thalès
I – Points alignés :
Deux droites sont parallèles si elles n’ont aucun point commun ou si elles sont confondues.
Conséquence :
Si deux droites sont parallèles et possèdent un point commun alors elles sont confondues.
Cette propriété permet de démontrer que trois points sont alignés.
Exemple :
Soit deux droites parallèles (AB) et (AC). Comme le point A est commun à ces deux droites,
elles sont confondues. Donc A, B et C sont alignés.
II - Produit en croix :
On utilise le produit en croix pour résoudre des équations du style :
x 5
= .
3 6
6×x 5×3
5
On obtient 6 × x= 5 × 3 puis
=
soit x = .
6
6
2
Exemples : Résoudre les équations :
7x 7
3 6
4 2
a)
=
b) =
c) =
5 10
x 17
5 x
d)
9 x
=
4 3
III - Théorème de Thalès (théorème direct) :
a) Figures-clés :
N
A
M
A
C
A
M
B
N
B
C
C
(MN) // (BC)
N
B
(MN) // (BC)
M
(MN) // (BC)
1
3ème
Cours : Théorème de Thalès
b) Enoncé du Théorème de Thalès :
M ∈ (AB)

Soient ABC et AMN 2 triangles tels que N ∈ (AC)
(MN)//(BC)
AM AN MN
on a alors :
=
=
AB
AC
BC
c) Exemples :
Exemple 1 :
AM = 30 ; AB = 80 ; AC = 20.
Les droites (MN) et (BC) sont parallèles.
Calculer AN.
Réponse :
Les droites (MN) et (BC) étant parallèles, on peut appliquer le théorème de Thalès dans les
triangles AMN et ABC :
AM AN MN
=
=
AB AC BC
30 AN MN
Soit :
=
=
80 20 BC
Donc AN×80 = 30×20
30×20 30×20 30 15
D’où : AN =
=
=
=
= 7,5
80
4×20
4
2
2
3ème
Cours : Théorème de Thalès
Exemple 2 :
UV) // (JK).
IJ = 30 ; IK = 20 ; IU = 10 ; UV = 10.
Calculer IV et JK.
Réponse :
Les droites (UV) et (JK) étant parallèles, on peut appliquer le théorème de Thalès dans les
triangles IUV et IJK :
IJ IK JK
=
=
IV IU UV
Soit
30 20 JK
=
=
IV 10 10
Calcul de IV :
IV×20 = 30×10
30×10
D’où IV =
= 15
20
Calcul de JK :
Et JK×10 = 20×10
D’où : JK = 20
3
3ème
Cours : Théorème de Thalès
Exemple 3. (donné au brevet) :
(Allemagne 96)
Le dessin ci-dessous n'est pas en vraie grandeur.
Les droites (NM) et (FG) sont parallèles.
On donne les longueurs suivantes :
EM = 2,5 ; MN = 4 ; NG = 7 ; FG =12.
Calculer les longueurs MF et EN.
Réponse :
Les droites (MN) et (FG) étant parallèles, on peut appliquer le théorème de Thalès dans les
triangles EMN et EFG :
EM EN MN
=
=
EF EG FG
FG
12
×EM = ×2,5 = 7,5 et MF = EF – EM = 7,5-2,5 = 5
MN
4
EN
4 1
et
=
=
EN + 7 12 3
Donc 3 EN = EN + 7
Soit 2 EN = 7
Et EN = 3,5
Donc EF =
d) Conséquences sur les longueurs et les aires
Si deux triangles sont dans la configuration du théorème de Thalès,
les longueurs des côtés du triangle AMN sont proportionnelles aux longueurs des côtés
du triangle ABC :
AM = k AB
AN = k AC
MN = k BC
aire AMN = k² × aire ABC
Démonstration :
H et K sont les pieds des hauteurs issues de A, les
triangles AMK et ABH sont aussi dans la
configuration de Thalès : AK = k AH
1
1
AK × MN = k AH × k BC
2
2
1
Aire AMN = k² × AH × BC
2
Aire AMN = k² × aire ABC
Aire AMN =
4
3ème
Cours : Théorème de Thalès
IV - Réciproque du Théorème de Thalès :
a) Théorème :
Si ABC et AMN sont deux triangles tels que :
A, M, B et A, N, C sont alignés dans cet ordre
AM = AN
 AB AC
alors, les droites (MN) et (BC) sont parallèles.
b) Exemples
Exemple 1
AC = 11 ; AE = 22 ;
CB = 15 ; BF = 30.
Les droites (AB) et (EF) sont-elles parallèles ?
Réponse :
CE = AC + AE = 11 + 22 = 33
CF = CB + BF = 15 + 30 = 45
CA 11 1
CB 15 1
=
= et
=
=
CE 33 3
CF 45 3
CAB et CEF sont deux triangles tels que d’une part les points C, A, E et d’autre part les
CA CB
points C, B, F sont alignés dans cet ordre et
=
, donc selon la réciproque du théorème
CE CF
de Thalès les droites (AB) et (EF) sont parallèles.
Exemple 2
Démontre que les droites (MN) et (ST) sont
parallèles.
On donne OM = 2,8 cm ; ON = 5,4 cm ; OS = 2,7 cm et
OT = 1,4 cm.
Réponse :
OT 1,4 1
OS 2,7 1
=
= et
=
=
OM 2,8 2
ON 5,4 2
OST et ONM sont deux triangles tels que S, O, N et
OT OS
T, O, M sont alignés dans cet ordre et
=
, donc selon la réciproque du théorème de
OM ON
Thalès les droites (MN) et (ST) sont parallèles.
D’une part :
5
3ème
Cours : Théorème de Thalès
c) Conséquence du théorème de Thalès : montrer que deux droites ne sont pas parallèles
Si ABC et AMN sont deux triangles tels que :
A, M, B et A, N, C sont alignés dans cet ordre
AM ≠ AN
 AB AC
alors, les droites (MN) et (BC) ne sont pas parallèles.
Exemple :
On donne AB = 2,5 cm ; BC = 3,3 cm ; AC =
2,4 ; CD = 6 cm et CE = 9 cm.
Les droites (ED) et (AB) sont-elles
parallèles?
Justifie la réponse.
CA 2,4 24 12×2 2
=
=
=
=
6
60 12×5 5
CD
CB 3,3 33 11×3 11
D’autre part :
=
=
=
=
CE
9
90 30×3 30
2 12 11
CA CB
Or =
≠
donc
≠
5 30 30
CD CE
D’une part :
CAB et CDE sont deux triangles tels que A, C, D et B, C, E sont alignés dans cet ordre et
CA
CD
CB
, donc selon la conséquence du théorème de Thalès les droites (ED) et (AB) ne sont pas
CE
parallèles.
Remarque : la conséquence du théorème de Thalès se nomme aussi la contraposée du
théorème de Thalès.
≠
6
3ème
Cours : Théorème de Thalès
V – Constructions de points
La construction des points M d’une droite donnée (AB) tels que
AM
= k (k étant un nombre
AB
donné) est une application de la propriété de Thalès.
Exemple : construction des points M tels que
AM 3
=
AB 5
On trace le segment [AB] ainsi qu'une demi-droite d'origine A.
On gradue à l'aide du compas, cette demi-droite et on y place les points C et D d'abscisses
respectives 3 et 5.
On trace la droite (BD); on construit la droite parallèle à la droite (BD) passant par le point
C.
Enfin, on note M son point d'intersection avec la droite (AB).
Justification :
Les droites (MB) et (CD) sont sécantes en A.
Les droites (MC) et (BD) sont parallèles.
AM AC 3
Or, d'après le théorème de Thalès, on a :
=
= .
AB AD 5
7