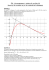
Correction DS2_TESL

CORRECTION DU DEVOIR N°2 DE MATHEMATIQUES
EXERCICE N°1 (5 points) QCM
1) La suite ‫ ݒ‬définie par ቊ
‫ݑ‬
ଵ
□ ‫ݑ‬ଵ = ଷ
‫ݑ‬଴ = 2
௡ାଵ
=
ଶ௨೙ ିଵ vérifie
௨೙ ାଶ
:
ଵ
ଷ
□ ‫ݑ‬ଵ = − ଶ
█ ‫ݑ‬ଵ = ସ
2) La suite ‫ ݑ‬définie pour tout entier ݊ par ‫ݑ‬௡ = 6݊ − 1 est :
□ arithmétique
□ géométrique
er
de raison 6 et de 1er
de raison −1 et de 1
terme ‫ݑ‬଴ = 6
terme ‫ݑ‬଴ = −1
█ arithmétique
de raison 6 et de 1er
terme ‫ݑ‬଴ = −1
□ géométrique
█ géométrique
3) La suite ‫ ݒ‬définie pour tout entier ݊ par ‫ݒ‬௡ =
ଷ೙
ହ
est :
□ géométrique
de raison 3 et de 1er
de
ଷ
terme ‫ݒ‬଴ =
ହ
ଷ
raison
ହ
et de 1er
de raison 3 et de 1er
ଵ
ଵ
terme ‫ݑ‬଴ = ହ
terme ‫ݑ‬଴ = ହ
4) ݂ est convexe sur [-2 ;1] puis concave sur [1 ; 4] et admet un point d’inflexion au point d’abscisse 1
donc on a :
□ ݂ ᇱ (1) = 0
□ ݂ ᇱᇱ (0) = 0
█ ݂ ᇱ ′(1) = 0
5) On a :
█ ݂ ᇱᇱpositive sur [−2 ; 1]
□ ݂ ᇱᇱ négative sur [−2 ; 0]
□ ݂ ᇱᇱ positive sur [−2 ; 3,5].
EXERCICE N°2 : Convexité d’une fonction (3 points)
1
f(x) :=10*x/(x+2)^2
2
g(x) :=deriver(f(x))
3
୶
x -> 10.( (୶ାଶ)² )
x ->
Soit ݂ la fonction définie sur l’intervalle [0 ; 10]
ିଵ଴.(୶ିଶ)
10‫ݔ‬
par ݂(‫ݔ( = )ݔ‬+2)² .
(୶ାଶ)య
h(x) :=deriver(g(x))
x ->
ଶ଴.(୶ିସ)
(୶ାଶ)ర
Certains élèves ont été gênés par le tableau de calcul formel.
En ligne 1, on entre la fonction ݂.
En ligne 2, on dérive la fonction ݂, le logiciel affiche ݃(‫ ݂ = )ݔ‬ᇱ (‫= )ݔ‬
ିଵ଴(௫ିଶ)
.
(௫ାଶ)య
En ligne 2, on dérive la fonction ݂′, le logiciel affiche ℎ(‫ ݂ = )ݔ‬ᇱᇱ (‫= )ݔ‬
1) Sur [0 ; 10] , étude du signe de ℎ(‫∶ )ݔ(’’݂ = )ݔ‬
pour tout ‫ ݔ‬de [0 ; 10] , ݂ ᇱᇱ (‫= )ݔ‬
tableau de signes : (1 point)
࢞
ࢌᇱᇱ (࢞)
0
ଶ଴(௫ିସ)
,
(௫ାଶ)ర
−
ଶ଴(௫ିସ)
.
(௫ାଶ)ర
comme (‫ ݔ‬+ 2)ସ > 0 alors ݂’’ est du signe (‫ ݔ‬− 4) d’où le
4
0
+
10
2) Etude de la convexité de la fonction ݂ : (1 point)
݂ ᇱᇱ est négative sur [0 ; 4] donc ݂’ est décroissante donc ࢌ est concave
concave sur [૙ ; ૝].
݂ ᇱᇱ est positive sur [4 ; 10] donc ݂’ est croissante donc ࢌ est convexe sur [૝ ; ૚૙].
3) ݂′′ s’annule en 4 en changeant de signe donc la courbe de ࢌ admet un point d’inflexion au point
d’abscisse 4. (0,5 point)
ଵ଴×ସ
Ce point a pour coordonnées (4 ; ݂(4)) or ݂(4) = (ସାଶ)మ =
Le point d’inflexion a pour coordonnées ቀ૝ ;
ସ଴
ଷ଺
૚૙
ቁ.. (0,5 point)
ૢ
=
ଵ଴
.
ଽ
EXERCICE N°3 : Position relative (4 points)
Soit la fonction ݃ définie sur [1 ; 5] par ݃(‫ ݔ = )ݔ‬ଷ − 6‫ݔ‬² + 11‫ ݔ‬− 8, de courbe représentative ‫ܥ‬௚ .
1) Equation réduite de la tangente ‫ ܦ‬à la courbe ݃ au point d'abscisse 2 ∶
‫ ܦ‬a pour équation ‫݃ = ݕ‬ᇱ (2)(‫ ݔ‬− 2) + ݃(2).
Or pour tout ‫ ݔ‬de [1 ; 5], ݃ᇱ (‫ = )ݔ‬3‫ݔ‬² − 12‫ ݔ‬+ 11 donc ݃’(2) = −1.
݃(2) = 8 − 24 + 22 − 8 = −2.
Donc ‫ = ݕ‬−(‫ ݔ‬− 2) − 2 soit ‫ = ݕ‬−‫ݔ‬.
ࡰ a pour équation ࢟ = −࢞.. (1 point)
2)
a. Pour tout ‫ ݔ‬de [1 ; 5], ݀(‫ )ݔ(݃ = )ݔ‬− (−‫)ݔ‬.
݀(‫ ݔ = )ݔ‬ଷ − 6‫ݔ‬² + 11‫ ݔ‬− 8 + ‫ݔ‬
݀(‫ ݔ = )ݔ‬ଷ − 6‫ݔ‬² + 12‫ ݔ‬− 8
Or (‫ ݔ‬− 2)ଷ = (‫ ݔ‬− 2)(‫ ݔ‬− 2)² = (‫ ݔ‬− 2)(‫ݔ‬² − 4‫ ݔ‬+ 4) = ‫ ݔ‬ଷ − 6‫ݔ‬² + 12‫ ݔ‬− 8
Donc pour tout ࢞ de [૚ ; ૞], ࢊ(࢞) = (࢞ − ૛)૜ . (1 point)
b. Etude du signe de ݀(‫ )ݔ‬sur [1 ; 5]: (0,5 point)
Pour tout ‫ ݔ‬de [1 ; 5], ݀(‫ )ݔ‬est du signe de ‫ ݔ‬− 2, d'où le tableau :
࢞
ࢊ(࢞)
1
−
2
0
+
5
c. Position relative de ‫ܥ‬௚ par rapport à ‫ ܦ‬sur [1 ; 5] ∶ (1 point)
݀(‫ ≤ )ݔ‬0 ⟺ ݃(‫ ≤ )ݔ‬−‫ ࢍ࡯ ⟺ ݔ‬est enPour ࢞ ∈ [૚ ; ૛],,
en-dessous de ࡰ.
Pour ࢞ ∈ [૛ ; ૞],,
݀(‫ ≥ )ݔ‬0 ⟺ ݃(‫ ≥ )ݔ‬−‫ ࢍ࡯ ⟺ ݔ‬est enen-dessus de ࡰ.
3) Comme la tangente au point d’abscisse 2 coupe la courbe en la traversant alors
le point d’abscisse 2 est un point d’inflexion pour la courbe ࡯ࢍ . (0,5 point)
PROBLEME : Etude d’une fonction coût total (8 points)
L’entreprise chinoise Shishi produit du tissu en coton qu’elle conditionne en « roules » de 2 000 m de
long et 1,5 m de large. Elle peut fabriquer au maximum 10 km en continu.
Le coût total de production, en euro, est donné en fonction de la longueur, en km, par la formule :
࡯(࢞) = ૚૞࢞૜ − ૚૛૙࢞² + ૞૙૙࢞ + ૠ૞૙ où ࢞ ∈ [૙ ; ૚૙]
PARTIE A : Etude du bénéfice
On a tracé sur la feuille annexe, la courbe ߁ de ‫ ܥ‬et ‫ܦ‬ଵ la droite d’équation ‫ = ݕ‬400‫ݔ‬.
1) Au vu du graphique, la courbe ߁ de ‫ ܥ‬est toujours au-dessus de la droite ‫ܦ‬ଵ donc pour tout ‫ ݔ‬de
[0 ; 10], ‫ > )ݔ(ܥ‬400‫ ݔ‬donc le coût est supérieur à la recette.
Donc l’entreprise Shishi ne peut pas réaliser un bénéfice si le prix du marché est égal à 400€
400€ par km. (0,5
point)
2) Dans cette question, on suppose que le prix du marché est égal à 680€ le km.
a. La droite ‫ܦ‬ଶ d’équation ‫ = ݕ‬680‫ ݔ‬passe par l’origine et le point de coordonnées (0 ; 3400).
Déterminer pour quelles quantité produites et vendues, l’entreprise Shishi réalise un bénéfice c’est
résoudre graphiquement ‫ > )ݔ(ܥ‬680‫ݔ‬. (1 point)
L’entreprise Shishi réalise un bénéfice si elle fabrique et vend entre 2,1 km et 8,7 km de tissu.
b. Soit ‫ ܤ‬la fonction définie sur [0 ; 10] par : ‫ = )ݔ(ܤ‬680‫ ݔ‬− ‫)ݔ(ܥ‬.
Pour tout ‫ ݔ‬de[0 ; 10], ‫ = )ݔ(ܤ‬680‫ ݔ‬− 15‫ ݔ‬ଷ + 120‫ݔ‬² − 500‫ ݔ‬− 750 = −15‫ ݔ‬ଷ + 120‫ݔ‬² + 180‫ ݔ‬− 750
Donc ࡮’(࢞) = −૝૞࢞² + ૛૝૙࢞ + ૚ૡ૙. (0,5 point)
c. Etude des variations de ‫ ܤ‬sur [0 ; 10] ∶ (1,5 point)
‫ ’ܤ‬est un polynôme de degré 2.
∆= 240² − 4 × (−45) × 180 = 90 000 = 300²
Deux racines ‫ݔ‬ଵ =
ିଶସ଴ିଷ଴଴
ିଶ×ସହ
= 6 et ‫ݔ‬ଶ =
ିଶସ଴ାଷ଴଴
ିଶ×ସହ
‫ ’ܤ‬est positive sur [0 ; 6] et négative sur [6 ; 10].
࢞
࡮′(࢞)
0
=−
ଶ
ଷ
6
+
0
2160
࡮(࢞)
−
10
L’entreprise Shishi réalise un bénéfice maximum avec un prix du marché
marché de 680€
680€ le km pour 6 km de
tissu vendu. (0,5 point)
PARTIE B : Etude du coût marginal
Le coût marginal ‫ܥ‬௠ est assimilé à la fonction dérivée du coût total donc on pose, pour tout ‫ ݔ‬de
[0 ; 10], ‫ܥ‬௠ (‫ ܥ = )ݔ‬ᇱ (‫)ݔ‬.
1) Etudier des variations de ‫ܥ‬௠ sur [0 ; 10]: (1 point)
‫ܥ‬௠ (‫ ܥ = )ݔ‬ᇱ (‫ = )ݔ‬45‫ݔ‬² − 240‫ ݔ‬+ 500
ᇱ
ᇱ (‫)ݔ‬
Donc ‫ܥ‬௠
(‫ = )ݔ‬90‫ ݔ‬− 240 et ‫ܥ‬௠
=0⟺‫=ݔ‬
ଶସ଴
ଽ଴
଼
= ଷ on en déduit le tableau :
࢞
0
࡯′࢓ (࢞)
6
−
0
10
+
࡯࢓ (࢞)
଼
ଷ
‫ܥ‬௠ admet un minimum en .
2) Etude de la convexité de ‫ ܥ‬: (0,5 point)
଼
଼
‫ܥ‬௠ = ‫ ܥ‬ᇱ est décroissante surቂ0 ; ଷቃ donc ‫ ܥ‬est concave sur ቂ0 ; ଷቃ.
଼
଼
‫ܥ‬௠ = ‫ ܥ‬ᇱ est croissante surቂଷ ; 10ቃ donc ‫ ܥ‬est convexe sur ቂଷ ; 10ቃ.
Donc la courbe ࢣ admet un point d’inflexion en
ૡ
valeur en laquelle ࡯࢓
૜
admet un minimum.
PARTIE C : Etude du coût moyen
Le coût moyen ‫ ܯܥ‬mesure le coût par unité produite. Donc pour tout ‫ ݔ‬de [0 ; 10], ‫= )ݔ(ܯܥ‬
1) Prouver que pour tout ‫ ݔ‬de [0 ; 10],
‫= )ݔ(ܯܥ‬
15‫ݔ‬3 −120‫ݔ‬2 +500‫ݔ‬+750
௫
= 15‫ݔ‬² − 120‫ ݔ‬+ 500 +
Donc ‫ܯܥ‬ᇱ (‫ = )ݔ‬30‫ ݔ‬− 120 −
଻ହ଴
௫²
=
ଷ଴௫ య ିଵଶ଴௫²ି଻ହ଴
஼(௫)
.
௫
଻ହ଴
௫
௫²
Or 30(‫ ݔ‬− 5)(‫ ݔ‬+ ‫ ݔ‬+ 5) = (30‫ ݔ‬− 150)(‫ݔ‬² + ‫ ݔ‬+ 5) = 30‫ ݔ‬ଷ − 120‫ݔ‬² − 750
ଶ
Donc ࡯ࡹᇱ (࢞) =
2)
૜૙(࢞ି૞)(࢞૛ ା࢞ା૞)
࢞²
. (1 point)
a. Pour quelle longueur ‫ݔ‬଴ de tissu produite le coût moyen est-il minimum ?
Pour tout ‫ ݔ‬de ]0 ; 10], ‫ܯܥ‬′ (‫ )ݔ‬est du signe de ‫ ݔ‬− 5 (‫ݔ‬² + ‫ ݔ‬+ 5 > 0 et ‫ݔ‬² > 0).
Donc ‫ܯܥ‬ᇱ est négative sur ]0 ; 5] et positive sur [5 ; 10] donc ‫ ܯܥ‬admet un minimum en 5.
Le coût moyen est donc minimum pour ࢞૙ = 5 km de tissu vendu. (0,5 point)
Que valent dans ce cas le coût moyen, le coût total et le coût marginal ? (0,75 point)
‫(ܯܥ‬5) =
஼(ହ)
ହ
= 425
‫(ܥ‬5) = 2125
‫ܥ‬௠ (5) = 425
Donc le coût moyen est de 425€
425€ par km de tissu, le coût
coût total est de 2125€
2125€ et le coût
coût marginal est de
425€.
425€.
b. Si le prix du marché est de 680€ le km, quel est le bénéfice réalisé par l’entreprise si elle
fabrique et vend une longueur de tissu de ‫ݔ‬଴ km ? (0,25 point)
‫(ܤ‬5) = 1275
Donc le bénéfice réalisé est de 1275€.
1275€.
Voici l’annexe :