Proposition de corrigé avec le Classpad 300

Sujet 044
Épreuve pratique de mathématiques au Bac S
(expérimentation 2006/2007)
Corrigé
Proposition de corrigé avec le Classpad 300
1. Pour tout n de N, on a Vn =
n(n + 1)
.
2
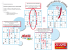
2. On va travailler dans l’environnement
. On nomme n3 la première colonne (elle va
3
contenir les n ) et Sn la seconde (qui va contenir les Sn ).
Dans la case de calcul de la première colonne, on entre seq(n^3,n,1,30). Cette colonne
se remplit alors avec les cubes des entiers de n = 1 à n = 30.
Dans la case de calcul de la seconde colonne, on entre cuml(n3). Cette colonne se remplit
alors avec les cumuls de la liste n3, c’est-à-dire avec les Sn de n = 1 à n = 30 (fig1).
fig1 : la colonne des Sn
fig2 : la colonne des vn2
fig3 : calcul formel
3. On crée une troisième colonne, baptisée ici vn2. Dans la case de calcul correspondante,
on entre l’expression sum(n^2(n+1)^2/4,n,1,30).
Le résultat (faire défiler le tableau pour en avoir la confirmation jusqu’à la valeur n = 30)
indique que (du moins dans l’intervalle 1 6 n 6 30) on a l’égalité Sn = Vn2 (fig2).
n2 (n + 1)2
pour tout n > 1.
4
k=1
Puisque S1 = 1 et V1 = 1, la propriété est vraie si n = 1.
4. On va prouver que Sn = Vn2 , c’est-à-dire
n
P
k3 =
Supposons qu’elle soit vraie pour un entier n > 1 donné. Alors :
n2 (n + 1)2
Sn+1 = Sn + (n + 1)3 =
+ (n + 1)3
4
(n + 1)2 (n + 2)2
(n + 1)2 2
2
(n + 4(n + 1)) =
= vn+1
=
4
4
La propriété est donc vraie au rang n + 1, ce qui achève la récurrence.
On voit (fig3) comment vérifier cette égalité dans l’application
c Jean-Michel Ferrard, pour Casio France
°
.
Page 111
Sujet 044
Épreuve pratique de mathématiques au Bac S
(expérimentation 2006/2007)
Complément :
n
P
∗
Si on pose xk = k pour tout k de N , on a donc l’égalité
k=1
x3k
=
Corrigé
³P
n
xk
´2
.
k=1
Il est intéressant de constater que la réciproque est vraie, sous réserve de supposer que
les xk sont des réels strictement positifs.
L’exercice est un joli exemple de récurrence forte, et il est sans très difficile pour un élève
de terminale S.
Enoncé :
Soit (xk )k>1 une suite de R+∗ .
³P
´2
n
n
P
3
xk .
On suppose que pour tout entier n > 1, on a l’égalité
xk =
k=1
k=1
Montrer que pour tout entier k on a xk = k.
Solution :
On a bien x1 = 1 car
1
P
k=1
x3k =
³P
1
k=1
xk
´2
⇒ (x31 = x21 ) ⇒ (x1 = 1) (rappel : x1 > 0.)
On se donne maintenant un entier n > 1, et on suppose que l’égalité xk = k est vraie
pour tout entier k de {1, . . . , n} (hypothèse de récurrence forte).
Nous allons montrer l’égalité xn+1 = n + 1.
³
´2
n
n+1
n
P
P 3 ³n+1
P ´2
P
xk =
xk donc : x3n+1 +
x3k = xn+1 +
xk .
Par hypothèse, on a
k=1
k=1
k=1
k=1
En utilisant l’hypothèse de récurrence cette égalité s’écrit aussi :
µ
¶2
³
´2
n
n
P
P
n(n + 1)
n2 (n + 1)2
3
3
3
xn+1 +
= xn+1 +
.
k = xn+1 +
k c’est-à-dire : xn+1 +
4
2
k=1
k=1
Après développement, on obtient x3n+1 − x2n+1 − n(n + 1)xn+1 = 0.
Cette expression se factorise en xn+1 (xn+1 + n)(xn+1 − n − 1) = 0. Sachant que xn+1 > 0,
il vient xn+1 = n + 1, ce qui prouve la propriété au rang n + 1 et achève la récurrence.
c Jean-Michel Ferrard, pour Casio France
°
Page 112