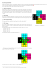Musterlösung 8 - D-MATH

Dr. T. Bühler
M. Wellershoff
Frühlingssemester 2016
Komplexe Analysis D-ITET
ETH Zürich
D-MATH
Serie 8
Aufgabe 8.1
Umlaufzahlen Berechnen - Teil I
Das Ziel der Aufgabe ist es die Umlaufzahlen in vier Zyklen zu berechnen. Damit klar ist was
genau gemacht werden soll, gibt es zu jeder Teilaufgabe ein kleines Beispiel.
(8.1a)
Zeichne vier jeweils verschiedene Zyklen.
Als Beispiel betrachte den Zyklus in Abbildung 8.1.
Abbildung 8.1: Ein Beispiel für einen Zyklus.
(8.1b) Berechne alle vorkommenden Umlaufzahlen innerhalb der vier Zyklen, die du in Aufgabe (8.1a) gezeichnet hast.
Für den Zyklus in Abbildung 8.1 sähe das so aus wie in Abbildung 8.2.
Aufgabe 8.2
Umlaufzahlen Berechnen - Teil II
Fixiere n, k ∈ Z und r > 0 mit r 6= 1. Bestimme die Umlaufzahl des geschlossenen Weges
γ(t) := e2πint + re2πikt ,
0≤t≤1
um den Nullpunkt. In anderen Worten: Bestimme indγ (0).
H INWEIS : Gibt es eine Homotopie, welche den kleineren Kreis auf null zusammenzieht, ohne
dabei über den Ursprung zu gehen?
Lösung: Zuerst wollen wir den Fall r < 1 untersuchen. Wir betrachten den Hinweis und merken,
dass es eine Homotopie H : [0, 1]2 → C gibt, welche den kleineren der beiden Kreise auf null
zusammenzieht. Diese ist gegeben durch
H(λ, t) := λ(e2πint + re2πikt ) + (1 − λ)(1 + r)e2πint .
Problem Sheet 8
Page 1
Problem 8.1
0
1
2
2
1
3
2
1
2
1
0
−1
Abbildung 8.2: Der Zyklus aus Abbildung 8.1 mit Umlaufzahlen.
Um zu überprüfen, dass dies eine Homotopie ist, bemerken wir zuerst, dass H stetig ist. Desweiteren gilt
H(0, t) = (1 + r)e2πint ,
H(1, t) = γ(t),
H(λ, 0) = 1 + r = H(λ, 1).
und somit ist H eine Homotopie. Nun wollen wir die Homotopieversion des Satzes von Cauchy
anwenden (siehe zum Beispiel: Freitag, Busam: ’Funktionentheorie 1’, dritte Auflage, Theorem
A5, s. 236). Betrachte zuerst einmal das Integral, welches wir berechnen wollen
Z
dz
.
indγ (0) =
γ z
Man sieht also, dass wir, um die Homotopieversion des Integralsatzes zu nutzen, zuerst zeigen
müssen, dass unsere Homotopie nicht durch die Singularität bei null geht. Betrachte also
H(λ, t) = 0 ⇔ λ(e2πint + re2πikt ) = −(1 − λ)(1 + r)e2πint .
Dies ist der Fall genau dann, wenn
1
1+r
·
.
2πi(k−n)t
r
1−e
Diese Gleichung kann aber nicht gelten für λ ∈ (0, 1), da t = 12 gelten muss, damit die rechte
Seite überhaupt eine reelle Zahl ist und somit
1+r
> 1.
λ=
2r
Nun können wir also die Homotopieversion des Satzes von Cauchy anwenden und erhalten
Z
Z
Z
dz
dz
dz
indγ (0) =
=
=
= n.
γ z
H(1,·) z
H(0,·) z
λ=
Für den zweiten Fall (r > 1) können wir nun ein sehr ähnliches Argument anführen, um zu
zeigen, dass
indγ (0) = k.
Die Homotopie ist in diesem Falle, gegeben durch
H(λ, t) := λ(e2πint + re2πikt ) + (1 − λ)(1 + r)e2πikt .
Problem Sheet 8
Page 2
Problem 8.2
Aufgabe 8.3
(8.3a)
Anwendungen des Residuensatzes
Betrachte die Funktion
f (z) :=
1
1 + z2
und die Wege
γk (t) := ei
πk
2
+ e2πit ,
0 ≤ t ≤ 1.
Berechne die Integrale
Z
f (z) dz.
γk
Lösung: Wir berechnen die Residuen in den beiden Polen z1 = i und z2 = −i von f . Bemerke
dazu, dass beide Pole Vielfachkeit 1 haben und dass wir deswegen mit g(z) := z 2 + 1 haben, dass
1
,
2i
−1
1
=
Res−i f = 0
g (−i)
2i
Resi f =
1
g 0 (i)
=
gilt. Nun wenden wir den Residuensatz an und erhalten
Z
Z
1
f (z) dz = 2πi · Resi (f ) · indγ1 (i) = 2πi · · 1 = π,
f (z) dz = 0,
2i
γ1
γ2
Z
Z
−1
· 1 = −π,
f (z) dz = 2πi · Res−i (f ) · indγ3 (−i) = 2πi ·
f (z) dz = 0.
2i
γ3
γ4
(8.3b)
Betrachte erneut
f (z) :=
1
.
1 + z2
Diesmal definieren wir den Weg
γ(t) := 2e2πit ,
Berechne erneut den Wert von
0 ≤ t ≤ 1.
Z
f (z) dz.
γ
Lösung: Wir benutzen, was wir in Aufgabe (8.3a) bereits berechnet haben und bekommen daher
mit dem Residuensatz
Z
1
1
f (z) dz = 2πi(Resi (f ) · indγ (i) + Res−i (f ) · indγ (−i)) = 2πi
−
= 0.
2i 2i
γ
(8.3c)
Bestimme die Menge der Nullstellen der Funktion
1
f (z) := e z − 1.
Lösung: Wir bemerken, dass die Funktion f eine Nullstelle in z ∈ C hat genau dann, wenn
1
e z = 1.
Man sieht also leicht, dass die Nullstellenmenge der Funktion f gegeben ist durch
1 N :=
n ∈ Z \ {0} .
2πin Problem Sheet 8
Page 3
Problem 8.3
(8.3d)
Wir definieren den Weg
7
γ(t) := i + eit ,
8
0 ≤ t ≤ 2π.
Berechne das Integral
1
Z
ez
1
γ
z 2 (e z − 1)
dz.
Lösung: Der Weg γ entspricht der Parametrisierung des Kreises mit Mittelpunkt z0 = i und
Radius r = 78 . Somit ist insbesondere z1 = 2πi die einzige Nullstelle des Nenners die von γ
umlaufen wird, da der Nenner genau z 2 f (z) entspricht, wobei f wie in Aufgabe (8.3c) definiert
ist. Um das Residuum des Integranden an z1 zu berechnen, bemerken wir, dass
f 0 (z1 ) =
−1 z1
· e 1 = 4π 2 6= 0
z12
gilt. Somit ist z1 ein Pol erster Ordnung und wir erhalten mit g(z) := z 2 f (z), dass
1
Resz1
ez
1
z 2 (e z
− 1)
=
1
g 0 (z1 )
=
1
= −1
2z1 f (z1 ) + z12 f 0 (z1 )
gilt. Wir wenden nun den Residuensatz an und erhalten
1
Z
ez
1
γ
(8.3e)
z 2 (e z − 1)
1
dz = 2πi · Resz1
Betrachte
!
1
z 2 (e z − 1)
· indγ (z1 ) = −2πi.
z
.
(z − 1)(z − 2)
f (z) :=
Welche Werte kann
ez
Z
f (z) dz
γ
annehmen, wenn γ irgendein geschlossener Weg ist, der weder z1 = 1 noch z2 = 2 durchläuft?
Lösung: Wir berechnen zuerst die Residuen in den Polen erster Ordnung z1 = 1 und z2 = 2.
Diese sind
Res1 f = −1,
Res2 f = 2.
Mit dem Residuensatz erhalten wir
Z
f (z) dz = 2πi(Res1 (f ) · indγ (1) + Res2 (f ) · indγ (2)).
γ
In der Vorlesung hatten wir gesehen, dass indγ (z) ∈ Z für alle z ∈ C \ {im(γ)}. Wir folgern
daraus, dass
Z
f (z) dz ∈ {2πin | n ∈ Z}.
γ
Das Integral kann also alle Werte aus 2πiZ annehmen.
Problem Sheet 8
Page 4
Problem 8.3
Aufgabe 8.4
Der Satz von Casorati-Weierstrass
Das Ziel der Aufgabe ist es den Satz von Casorati-Weierstrass zu beweisen. Bevor wir dies in
Angriff nehmen sind zwei Definitionen von Nöten:
• Eine Singularität einer Funktion f heisst wesentlich,
wenn sie weder hebbar noch ein Pol
1
ist. Ein gutes Beispiel dafür ist die Funktion sin z , welche in z = 0 eine Singularität hat,
die weder ein Pol noch hebbar ist.
• Eine Menge M heisst dicht, wenn jeder Ball Br (z0 ), für r > 0 und z0 ∈ C, einen Punkt
aus M enthält.
Der Satz von Casorati-Weierstrass lautet:
Sei z0 ∈ U ⊂ C eine wesentliche Singularität der analytischen Funktion f : U → C und
B (z0 ) \ {z0 } ⊂ U
eine punktierte -Umgebung von z0 , für > 0. Dann gilt, dass
M := f (B (z0 ) \ {z0 })
dicht in C ist.
H INWEIS : Wenn der Satz von Casorati-Weierstrass nicht gilt, so gibt es ein δ > 0 und ein ω0 ∈ C,
sodass Bδ (ω0 ) keinen Punkt aus M enthält. Schliesse aus dem Riemannschen Hebbarkeitssatz,
dass
1
h(z) =
f (z) − ω0
in z0 eine hebbare Singularität hat.
Lösung: Wir folgen dem Hinweis. Beachte, dass f nicht konstant ist, denn sonst wäre die Singularität in z0 sicher hebbar. Wenn Bδ (ω0 ) keine Punkte aus M enthält, so ist h beschränkt in
B (z0 ) \ {z0 } (um genau zu sein durch 1δ ). Dank dem Riemannschen Hebbarkeitssatz ist die Singularität von h in z0 hebbar. Damit ist h(z0 ) 6= 0 oder z0 ist eine Nullstelle endlicher Ordnung,
(wäre z0 eine Nullstelle unendlicher Ordnung, dann wäre h(z) ≡ 0, und somit wäre auch f (z)
konstant). Damit folgt aber nun, dass
f (z) =
1
+ ω0
h(z)
in z0 auch keine wesentliche Singularität haben kann, denn f (z0 ) ist entweder definiert oder z0
ist ein Pol endlicher Ordnung.
Publiziert am 25.April.
Einzureichen am 4. Mai.
Letzte Modifikation: 5. Mai 2016
Problem Sheet 8
Page 5
Problem 8.4