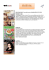EX 1 : ( 3 points ) On considère la suite (un) définie par { u0 = 1 = un

TS. Évaluation 3.09 - Correction
E X 1 : ( 3 points )
♣
On considère la suite (u n ) définie par
½
u0
u n+1
= 1
= u n + 2n + 3 pour tout entier naturel n.
1. Étudier la monotonie de la suite (u n ).
On a pour tout n ∈ N, u n+1 = u n + 2n + 3,
donc
u n+1 − u n = 2n + 3.
Or 2n + 3 > 3 > 0, donc u n+1 − u n > 0 quel que soit n ∈ N.
2.
Conclusion : la suite (u n ) est strictement croissante.
a. Démontrer que, pour tout entier naturel n, u n > n 2 .
Démonstration par récurrence :
– Initialisation : u 0 = 1 donc u 0 > 02 : la proposition est vraie pour n = 0 ;
– Hérédité : supposons qu’il existe n ∈ N tel que u n > n 2
je suppose la proposition vraie au rang n
alors u n + 2n + 3 > n 2 + 2n + 1 + 2
ou encore u n+1 > (n + 1)2 + 2 donc à fortiori u n+1 > (n + 1)2
alors la proposition est vraie au rang n + 1
– Conclusion : la proposition est vraie pour n = 0 , elle est héréditaire
donc par récurrence on a : pour tout n ∈ N, u n > n 2
b. Quelle est la limite de la suite (u n ) ?
Pour tout n ∈ N, u n > n 2
comme lim n 2 = +∞
n→+∞
on a par comparaison : lim u n = +∞.
n→+∞
2
Soit la suite (u n ) définie pour n ≥ 1 par u n+1 = u n − 3 et u 1 = 0 . Pour n ≥ 1 , on pose v n = u n + 5 .
5
1. Montrer que (v n ) est une suite géométrique. Préciser la raison.
E X 2 : ( 3 points )
Pour n ≥ 1 , on a :
2
2
v n+1 u n+1 + 5 5 u n − 3 + 5 5 u n + 2
=
=
=
=
vn
un + 5
un + 5
un + 5
2
5
× (u n + 5)
=
2
5
(u n + 5)
2
donc la suite (v n ) est une suite géométrique de raison q =
en effet, on a :
5
v n+1 =
2
vn
5
pour n ≥ 1
2. Soit n ≥ 1 , exprimer v n en fonction de n.
2
Comme (v n ) est géométrique de premier terme v 1 = u 1 + 5 = 0 + 5 = 5 et de raison q =
5
µ ¶n−1
2
n−1
j’obtiens pour n ≥ 1 : v n = v 1 × q
= 5×
5
3. Exprimer u n en fonction de n. En déduire lim u n .
n→+∞
un = v n − 5
donc
lim u n = lim v n − 5 = −5
n→+∞
n→+∞
avec
lim v n = lim 5 ×
n→+∞
n→+∞
µ ¶n−1
2
=0
5
car −1 <
2
<1
5
¶
2
6
E X 3 : ( 4 points ) On considère la suite (u n )n∈N définie par : u 0 = 5 et, pour tout entier n > 1, u n = 1 +
u n−1 +
n
n
1.
a. Calculer u 1 .
¶
µ
6
2
u 1 = 1 + u 0 + = 3 × 5 + 6 = 21
1
1
b. Les valeurs de u 2 , u 3 , u 4 , u 5 , u 6 , u 7 , u 8 , u 9 , u 10 , u 11 sont respectivement égales à :
45, 77, 117, 165, 221, 285, 357, 437, 525, 621.
À partir de ces données conjecturer la nature de la suite (d n )n∈N définie par d n = u n+1 − u n .
µ
J’obtiens : d 1 = u 1 − u 0 = 16 ,
d 2 = u 2 − u 1 = 24 ,
puis d 3 = 32 ,
d 4 = 40 ,
d 5 = 48 ,
on peut donc conjecturer que la suite (d n )n∈N est arithmétique de raison 8 et de premier terme 16.
TS. Évaluation 3.09 - Correction
♣
2. On considère la suite arithmétique (v n )n∈N de raison 8 et de premier terme v 0 = 16.
Justifier que la somme des n premiers termes de cette suite est égale à 4n 2 + 12n.
Soit (v n )n∈N la suite arithmétique de raison r = 8 et de premier terme v 0 = 16
Pour tout entier naturel n,
v n−1 = v 0 + (n − 1) r = 16 + 8 (n − 1) = 8 + 8n
La somme S n des n premiers termes est :
S n = v 0 + v 1 + · · · + v n−1 = n
µ
¶
³v +v
´
16 + 8 + 8n
0
n−1
=n
= n (12 + 4n) = 4n 2 + 12n
2
2
3. Démontrer par récurrence que pour tout entier naturel n on a : u n = 4n 2 + 12n + 5.
Démonstration par récurrence :
– Initialisation : u 0 = 5 = 4 × 02 + 12 × 0 + 5 : la proposition est vraie pour n = 0
2
– Hérédité : supposons
qu’il
¶ existe n ∈ Nµtel que u n¶ = 4n + 12n + 5.
µ
¡ 2
¢
6
6
2
2
4n + 12n + 5 +
un +
= 1+
.
alors u n+1 = 1 +
n +1
n +1
n +1
n +1
je suppose la proposition vraie au rang n
or 4n 2 + 12n + 5 = 4(n + 1)2 − 8n − 4 + 12n + 5 = 4(n + 1)2 + 4n + 1 = 4(n + 1)2 + 4(n + 1) − 3.
En reportant dans u n+1 au dessus, on obtient :
µ
¶
£
¤
2
6
u n+1 = 1 +
4(n + 1)2 + 4(n + 1) − 3 +
n +1
n +1
6
6
2
= 4(n + 1) + 4(n + 1) − 3 + 8(n + 1) + 8 −
+
= 4(n + 1)2 + 12(n + 1) + 5.
alors la proposition est vraie au rang n + 1
n +1 n +1
– Conclusion : la proposition est vraie pour n = 0 , elle est héréditaire
donc par récurrence on a, quel que soit n ∈ N, u n = 4n 2 + 12n + 5.
4. Valider la conjecture émise à la question 1. b..
Soit n ∈ N, d’après les questions précédentes :
¡
¢
d n = u n+1 − u n = 4(n + 1)2 + 12(n + 1) + 5 − 4n 2 + 12n + 5 = 4n 2 + 8n + 4 + 12n + 12 − 4n 2 − 12n − 5 = 16 + 8n = v 0 + nr = v n
La suite (d n )n∈N est arithmétique de raison 8 et de premier terme d 0 = 16.