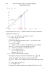Corrigé : ECRICOME 2001

Corrigé : ECRICOME 2001
Option économique
Exercice 1:
I. Puissances successives de la matrice


1 − 2b − 2a + 6ab
a + b − 3ab
a + b − 3ab
1. M (a)M (b) =  a + b − 3ab
1 − 2b − 2a + 6ab
a + b − 3ab  = M (a + b − 3ab)
a + b − 3ab
a + b − 3ab
1 − 2b − 2a + 6ab
2. On remarque que M (0) = I3 donc s’il existe b tel que a + b − 3ab = 0 alors la matrice sera inversible d’inverse M (b).
1
a
Or a + b − 3ab = 0 ⇔ (3a − 1)b = a donc si a 6= , il existe un unique b =
tel que M (a)M (b) = I3 .
3
3a − 1
1
On a donc montré que pour a 6= la matrice est inversible.
3
a
De plus M (a)−1 = M
.
3a − 1


1/3 1/3 1/3
De plus M (1/3) = 1/3 1/3 1/3. Comme toutes les lignes sont identiques M (1/3) n’est pas inversible.
1/3 1/3 1/3
En conclusion M (a) est inversible si et seulement si a 6=
1
3
3. On remarque que la matrice M (a) est une matrice symétrique, donc d’après le cours elle est diagonalisable.
4. D’après la question 1. [M (a)]2 = M (2a − 3a2 ) donc
[M (a)]2 = M (a) ⇔ 2a − 3a2 = a ⇔ a(1 − 3a) = 0 ⇔ a = 0 ou a =
On a donc a0 =

1
1
1
5. P =
3
1
1
= a0
3
1
.
3



1 1
2 −1 −1
1
1 1 et Q = −1 2 −1.
3
1 1
−1 −1 2
a) Pour tout réel α on a :
1
2
+α
3
 1 α3
P + αQ = 
3− 3

1 α
−
3
3
1 α
−
3
3
1
2
+α
3
3
1 α
−
3
3
1 α
−
3
3 
1 α
− 
3
3 

1
2
+α
3
3
1
(1 − α) = a, c’est-à-dire α = 1 − 3a on a bien M (a) = P + αQ.
3
b) P 2 = [M (a0 )]2 = M (a0 ) = P
QP = (I − P )P = P − P 2 = 0
P Q = P (I − P ) = P − P 2 = 0
Q2 = (I − P )2 = I − 2P + P 2 = I − P = Q
Ainsi en prenant
c) Comme QP = P Q = 0 les matrices P et Q commutent donc on peut appliquer la formule du binôme de Newton :
n
n
[M (a)] = (P + αQ) =
n X
n
k=0
k
P k (αQ)n−k = P n + (αQ)n = P + αn Q
On n’a gardé ici que deux termes dans la somme car comme P Q = 0 on a aussi P k Qn−k = 0 dès que k 6= 0 et
k 6= n. De plus comme P 2 = P et Q2 = Q, on a pour tout n, P n = P et Qn = Q.
On a donc [M (a)]n = P + αn Q.

1 + 2(1 − 3a)n 1 − (1 − 3a)n
1
n
1 − (1 − 3a)n 1 + 2(1 − 3a)n
d) [M (a)] =
3
1 − (1 − 3a)n
1 − (1 − 3a)n

1 − (1 − 3a)n
1 − (1 − 3a)n 
1 + 2(1 − 3a)n
II. Évolution d’un titre boursier au cours du temps
ECRICOME 2001
Page 1
Corrigé


pn
1. a) Notons Xn = qn . On remarque que Xn+1 = M (a)Xn .
rn
Montrons par récurrence que pour tout n > 1, Xn = [M (a)]n−1 X1 .
• Rang 1 : on a bien X1 = [M (a)]0 X1
• Soit n fixé. Supposons que Xn = [M (a)]n−1 X1 . On a alors :
Xn+1 = M (a)Xn = M (a)[M (a)]n−1 X1 = [M (a)]n X1
Grâce au principe de récurrence on a donc montré que pour tout entier n > 1, Xn = [M (a)]n−1 X1 .
On peut donc en déduire :

1


(1 + 2(1 − 3a)n−1 )p1 + (1 − (1 − 3a)n−1 )q1 + (1 − (1 − 3a)n−1 )r1
pn =


3

1
qn =
(1 − (1 − 3a)n−1 )p1 + (1 + 2(1 − 3a)n−1 )q1 + (1 − (1 − 3a)n−1 )r1

3



 rn = 1 (1 − (1 − 3a)n−1 )p1 + (1 − (1 − 3a)n−1 )q1 + (1 + 2(1 − 3a)n−1 )r1 3
2
b) Comme on sait que a ∈ 0;
on a 0 < 3a < 2 et donc −1 < 1 − 3a < 1 donc lim (1 − 3a)n−1 = 0. On peut donc
n→+∞
3
en déduire que les suites (pn ), (qn ) et (rn ) sont convergentes et :
lim pn =
n→+∞
p1 + q1 + r1
= lim qn = lim rn
n→+∞
n→+∞
3
2. a) • (Mn , Sn , Bn ) est un système complet d’événements donc d’après la formule des probabilités totales : P (Mn+1 ) =
P (Mn )PMn (Mn+1 ) + P (Sn )PSn (Mn+1 ) + P (Bn )PBn (Mn+1 )
2
1
1
Or d’après l’énoncé, PMn (Mn+1 ) = , PSn (Mn+1 ) = et PBn (Mn+1 ) = .
3
6
6
2
1
1
On a donc : P (Mn+1 ) = P (Mn ) + P (Sn ) + P (Bn )
3
6
6
1
2
1
• De même que précédemment on a P (Sn+1 ) = P (Mn ) + P (Sn ) + P (Bn ).
6
3
6
1
2
1
• et P (Bn+1 ) = P (Mn ) + P (Sn ) + P (Bn ).
6
6
3
b) On remarque que si on pose pn = P (Mn ), qn = P (Sn ) et rn = P (Bn ) on est dans la situation de la question 1 avec
1
a = et p1 = 0, q1 = 1 et r1 = 0. Donc on en déduit :
6

1

 P (Mn ) = (1 − (1/2)n−1 )


3

1
P (Sn ) = (1 + 2(1/2)n−1)

3



 P (Bn ) = 1 (1 − (1/2)n−1 )
3
c) Comme lim (1/2)n−1 = 0 on a
n→+∞
lim P (Mn ) = lim P (Sn ) = lim P (Bn ) =
n→+∞
n→+∞
n→+∞
1
3
Exercice 2:
I. Calcul du nombre moyen de composants défaillants entre les instants 0 et t.
1. Soit i ∈ {1, 2, · · · , n}. On sait que Ti suit la loi exponentielle de paramètre λ et on connait la fonction de répartition
d’une VAR suivant cette loi. On peut donc directement donner :
(
0
si t < 0
P (Ti < t) =
1 − e−λt si t > 0
2. Par définition on a tout d’abord Nt (Ω) = {0, · · · , n}. Le composant i est défaillant entre les instants 0 et t signifie que
sont temps de fonctionnement est inférieur strictement à t. Cet événement est donc de probabilité P (Ti < t) qui on
vient de le voir ne dépend pas de i.
Donc Nt compte le nombre de réalisation d’un événement de probabilité constante parmi les n composant. Nt suit donc
bien une loi binômiale de paramètres n et P (T1 < t).
De plus on a E(Nt ) = nP (T1 < t) = n(1 − e−λt ).
ECRICOME 2001
Page 2
Corrigé
3. On cherche dans cette question le premier instant t vérifiant E(Nt ) >
E(Nt ) >
n
2
⇔n(1 − e−λt ) >
n
2
n
2
1
2
⇔ − λt 6 − ln 2
ln 2
⇔t >
λ
⇔e−λt 6
ln 2
.
λ
II. Montage en série.
Donc on a t0 =
1. L’événement [Sn > t] signifie que tout les composant fonctionnaient au moins jusqu’à l’instant t et donc avaient tous
un temps de fonctionnement strictement supérieur à t. On a donc
[Sn > t] = [T1 > t] ∩ [T2 > t] ∩ · · · ∩ [Tn > t]
2. • On sait que pour tout réel t, Fn (t) = P (Sn 6 t). Or on a :
P (Sn 6 t) = 1 − P (Sn > t) = 1 − P ([T1 > t] ∩ [T2 > t] ∩ · · · ∩ [Tn > t])
Comme les VAR Ti sont indépendantes on a :
P ([T1 > t] ∩ [T2 > t] ∩ · · · ∩ [Tn > t]) = P (T1 > t) × P (T2 > t) × · · · × P (Tn > t)
= (1 − P (T1 6 t)) × (1 − P (T2 6 t)) × · · · × (1 − P (Tn 6 t))
(
(
1n
si t < 0
1
si t < 0
=
=
−λt n
−nλt
(e )
si t > 0
e
si t > 0
On en déduit donc :
Fn (t) =
(
0
1 − e−nλt
si t < 0
si t > 0
• On remarque que Fn est continue sur R car lim
Fn = lim
Fn = 0Fn (0) et que la continuité sur R∗ ne pose pas de
−
+
0
0
problème. De plus d’après les fonctions de référence Fn est de classe C 1 sur R∗ (peut être plus mais nous n’en n’avons
pas besoin) donc Fn est bien la fonction de répartition d’une VAR à densité et pour avoir une densité nous dérivons
Fn :
(
0
si t < 0
fn (t) =
nλe−nλt si t > 0
3. D’après la question précédente, on reconnait que Sn suit une loi exponentielle de paramètre nλ. On peut donc écrire :
E(Sn ) =
1
nλ
V (Sn ) =
1
(nλ)2
III. Montage en parallèle.
1. L’événement [Un < t] signifie que avant l’instant t tous les composant étaient défaillant, donc cela signifie qu’ils ont
tous un temps de fonctionnement strictement inférieur à t. On a donc
[Un < t] = [T1 < t] ∩ [T2 < t] ∩ · · · ∩ [Tn < t]
2. • On sait que pour tout réel t, Gn (t) = P (Un 6 t).
Comme les variables Ti sont indépendantes, on a
Gn (t) = P (Un 6 t) = P (T1 6 t) × P (T2 6 t) × · · · × P (Tn 6 t) =
(
0
(1 − e−λt )n
si t < 0
si t > 0
• On remarque que Gn est continue sur R car limGn = limGn = 0Fn (0) et que la continuité sur R∗ ne pose pas
0+
0−
de problème. De plus d’après les fonctions de référence Gn est de classe C 1 sur R∗ donc Gn est bien la fonction de
répartition d’une VAR à densité et pour avoir une densité nous dérivons Gn :
(
0
si t < 0
gn (t) =
nλe−λt (1 − e−λt )n−1 si t > 0
ECRICOME 2001
Page 3
Corrigé
3. gn est nulle sur ] − ∞; 0[ donc l’intégrale
n−1
X
Sur [0; +∞[, on peut écrire tgn (t) =
Z
k=0
Z
tgn (t) dt converge absolument et vaut 0.
−∞
nλ
Soit A > 0 :
0
n−1
(−1)k te−λ(k+1)t .
k
A
tgn (t) dt =
0
n−1
X
k=0
Z A
n−1
k
nλ
(−1)
te−λ(k+1)t dt
k
0
A
e−λ(k+1)A
1
1
A
−
→
lorsque A → +∞.
e−λ(k+1)A +
|te−λ(k+1)t | dt = −
2
2
λ(k + 1)
(λ(k + 1))
(λ(k + 1))
(λ(k + 1))2
0
Z +∞
tgn (t) dt converge absolument, ce qui signifie que Un admet bien une espérance et on a :
Donc l’intégrale
Or on a
Z
0
n−1
X
E(Un ) =
nλ
k=0
(n − 1)!
1
(−1)k
k!(n − 1 − k)!
(λ(k + 1))2
n−1
X
n!
1
(−1)k
(k + 1)!(n − 1 − k)!
λ(k + 1)
k=0
n−1
X (−1)k
n
=
k
+
1
λ(k + 1)
=
k=0
On a donc :
!
n−1
n
X
X (−1)k n (−1)k n + 1
−
(k + 1) k + 1
(k + 1) k + 1
k=0
k=0
!
n−1
(−1)n
1 X (−1)k
n+1
n
−
+
k+1
k+1
λ
(k + 1)
n+1
k=0
!
n−1
1 X (−1)k n
(−1)n
(formule du triangle de Pascal)
+
λ
(k + 1) k
n+1
k=0
n
1 X (−1)k n
λ
(k + 1) k
k=0
n
1 X (−1)k n + 1
(Transformation du coefficient binomial)
λ
(n + 1) k + 1
1
E(Un+1 ) − E(Un ) =
λ
=
=
=
=
k=0
n+1
X
1
n+1
(Changement d’indicei = k + 1)
(−1)i−1
i
λ(n + 1) i=1
!
n+1
X
1
n
+
1
+1
(−1)k−1
=
k
λ(n + 1)
=
k=0
1
1
(1 + (−1))n+1 + 1 =
=
λ(n + 1)
λ(n + 1)
formule du binôme
4. D’après la question précédente :
n−1
X
k=1
(E(Uk+1 ) − E(Uk )) =
n−1
X
k=1
1
λ(k + 1)
n
X
1
1
−
⇔E(Un ) − E(U1 ) =
λk
λ
k=1
Or U1 est en fait la variable T1 donc E(U1 ) =
1
et grâce à l’équivalent simple, on a
λ
E(Un )
ECRICOME 2001
∼
n→+∞
Page 4
ln n
λ
Corrigé
Exercice 3:
I. Étude d’un cas particulier
1
1
1
11
Dans cette partie : f1 (x) = +
+
−
x x+1 x+2
6
1. Pour éviter trop de photocopies le dessin n’est ici pas réalisé à l’échelle demandée dans l’énoncé.
y
1
0
x
1
1 1 11
+ −
= 0. On a donc ici déjà une racine de (E1 ).
2 3
6
3
−11x − 15x2 + 14x + 12
De plus f1 (x) =
. On connait une racine du numérateur donc on peut effectuer la division
6x(x + 1)(x + 2)
euclidienne du polynôme −11x3 − 15x2 + 14x + 12 par le polynôme x − 1. On obtient :
2. f1 (1) = 1 +
f1 (x) =
(x − 1)(11x2 + 26x + 12)
(x − 1)(−11x2 − 26x − 12)
=−
6x(x + 1)(x + 2)
6x(x + 1)(x + 2)
′
2
On va donc maintenant résoudre
11x2 + 26x + 12 = 0.Le
√ discriminant réduit est ∆ = 13 − 11 × 12 = 37, donc les
√
−13 − 37
−13 + 37
≈ −0, 63 et x2 =
≈ −1, 73.
racines sont : x1 =
11
11
Ainsi les racines de (E1 ) sont 1, x1 , x2 et ce résultat est cohérent avec notre graphique.
II. Dénombrement des racines de (En ).
1. Le domaine de définition de fn est Dn =] − ∞; −2n[∪] − 2n; −2n + 1[∪...∪] − 1; 0[∪]0; +∞[. La fonction fn est la somme
de fonctions strictement décroissantes et d’une fonction constante sur chacun des intervalles qui composent Dn . Donc
fn est strictement décroissante sur chacun des intervalles qui composent Dn .
On a lim fn (x) = −a et lim fn (x) = −a.
x→−∞
x→+∞
De plus pour tout entier k allant de 0 à 2n on a
lim fn (x) = −∞ et
x→−k−
x
fn (x)
2. • Comme
−∞
−a
−2n
−2n + 1
lim fn (x) = +∞
x→−k+
···
−1
+∞
ց
−∞
0
+∞
ց
−∞
···
+∞
+∞
ց
−∞
ց
−a
lim fn (x) = −a < 0 et fn strictement décroissante sur ] − ∞; −2n[, on a que pour tout x ∈] − ∞; −2n[,
x→−∞
fn (x) < 0 et donc fn ne s’annule pas sur cet intervalle.
• Pour tout entier k allant de 1 à 2n, on a lim fn (x) = +∞ et
x→−k+
lim
x→(−k+1)−
fn (x) = −∞ et fn est strictement
décroissante sur ] − k; −k + 1[ donc fn réalise une bijection de ] − k; −k + 1[ sur R et donc il existe un unique
ck ∈] − k; −k + 1[ tel que fn (ck ) = 0.
On a donc ici trouvé 2n racines de (En )
• De plus lim fn (x) = +∞ et lim fn (x) = −a < 0 et fn est strictement décroissante sur ]0; +∞[ donc fn réalise
x→0+
x→+∞
une bijection de ]0; +inf ty[ sur ] − a; +∞[ et donc il existe un unique b ∈]0; +∞[ tel que fn (b) = 0.
(En ) admet donc 2n + 1 racines.
ECRICOME 2001
Page 5
Corrigé
III. Limite de la plus grande des racines quand n tend vers +∞.
On note xn la plus grande des racines de (En ).
1. Précédemment nous avons montré qu’il existe une racine dans l’intervalle ]0; +∞[, donc la plus grande racine est
forcément dans cet intervalle et donc xn > 0.
2. • Pour cette première partie de question plusieurs méthodes possibles. En voici une parmi tant d’autres qui utilise que
si X > −1 et X 6= 0 alors ln(1 + X) < X.
1
x−1
1
1
1
x
. Or si x > 1 on a − > −1 et donc ln(1 − ) < − . On en
= − ln
= − ln 1 −
On remarque que ln
x−1
x
x
x
x
x
1
1
1
x−1
déduit que − ln(1 − ) > c’est-à-dire < ln
.
x
x
x
x
x
1
x
1
1
> 0, et ln
= ln(1 +
), on a ln
<
Comme de plus
x−1
x−1
x−1
x−1
x−1
x
1
1
<
.
On a donc pour tout x > 1, < ln
x
x−1
x−1
• D’après l’inégalité précédente on a, pour tout x > 0 et tout entier k allant de 1 à 2n :
x+k
1
1
< ln
<
x+k
x+k−1
x+k−1
On somme toutes ces inégalités pour toutes les valeurs de k possible :
2n
X
2n
2n
X
X
1
x+k
1
<
ln
<
x+k
x+k−1
x+k−1
k=1
k=1
k=1
! 2n−1
2n
X 1
Y x+k
1
<
⇔fn (x) − + a < ln
x
x+k−1
x+k
k=0
k=1
1
1
x + 2n
⇔fn (x) − + a < ln
< fn (x) −
+a
x
x
x + 2n
1
2n
1
< fn (x) −
+a
⇔fn (x) − + a < ln 1 +
x
x
x + 2n
En appliquant l’inégalité précédente pour x = xn on obtient :
1
2n
1
<a−
< ln 1 +
a−
xn
xn
xn + 2n
3. En utilisant l’inégalité de droite de l’encadrement précédent et le fait que a −
1
< a on a :
xn + 2n
2n
<a
ln 1 +
xn
2n
⇔1 +
< ea
xn
xn
1
⇔
> a
2n
e −1
2n
⇔xn > a
e −1
4. D’après la question précédente, lim xn = +∞ et d’après le théorème des gendarmes appliqué au dernier encadrement
n→+∞ 2n
de la question 2. on obtient : lim ln 1 +
= a.
n→+∞
xn
2n
2n
5. D’après la question précédente, on a donc lim 1 +
= ea . On peut donc en déduire que 1 +
∼ ea et par
n→+∞
xn
xn n→+∞
2
addition et multiplication on a donc xn ∼
n
n→+∞ ea − 1
ECRICOME 2001
Page 6
Corrigé