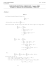Suites et Séries de Fonctions

Université Mohammed I
Année 2007-2008
Ecole Nationale des Sciences Appliquées
ENSA1 - Analyse II
Oujda
Enseignant : I.Elmahi
Chapitre 3
Suites et Séries
de Fonctions
Table des matières
I Suites de fonctions
1
1 Convergence simple, convergence uniforme des suites de fonctions
1
2 Théorèmes fondamentaux sur les suites de fonctions
3
II Séries de fonctions
7
1 Dénition
7
2 Convergence simple, convergence uniforme de séries de fonctions
7
1.1 Convergence simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Convergence uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1 Continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Intégration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Dérivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1 Critère de Cauchy de convergence uniforme dans un espace complet . . . . . . . .
2.2 Convergence normale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Condition susante de convergence uniforme . . . . . . . . . . . . . . . . . . . .
3 Théorèmes fondamentaux sur les séries de fonctions
3.1 Théorème de continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Théorème d'intégration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Théorème de dérivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
3
4
5
7
8
9
10
10
10
11
ENSA1
Analyse II
Suites et Séries de Fonctions
Suites et Séries de Fonctions
Première partie
Suites de fonctions
Soit (fn )n∈N une suite de fonction d'un ensemble ∆ non vide vers un corps K (K = R ou C)
fn : ∆ −→ K
x 7−→ fn (x)
1 Convergence simple, convergence uniforme des suites de fonctions
1.1 Convergence simple
Dénition
On dira que la suite de fonctions (fn ) converge simplement sur ∆ s'il existe f ∈ F(∆, K)
(appelée limite simple de la suite fn ) telle que :
∀x ∈ ∆;
lim fn (x) = f (x)
n→+∞
Ceci se traduit par :
(∀x ∈ ∆); (∀ε > 0) (∃N ∈ N) (∀n ≥ N ); |fn (x) − f (x)| ≤ ε
Exemples
fn : R −→ R
. On a :
nx2
x 7−→ fn (x) = 1+nx
n∈N
2
Pour x 6= 0 ; limn→+∞ fn (x) = 1.
Pour x = 0 ; fn (0) = 0 donc limn→+∞ fn (0) = 0.
La suite de fonctions (fn ) converge donc simplement vers la fonction f dénie par :
1 si x 6= 0
f : x 7−→ f (x) =
0 si x = 0
1. Soit
2. Soit le suite de fonctions
fn : R −→ R
.
2
x 7−→ fn (x) = nxe−nx + x
∀x ∈ R, on a
2
lim fn (x) = lim nxe−nx + x = x
n→+∞
n→+∞
Donc la suite de fonctions (fn ) converge simplement vers la fonction f dénie par : ∀x ∈
R; f (x) = x.
I.Elmahi
1
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
1.2 Convergence uniforme
Dénition
On dira que la suite de fonctions (fn ) converge uniformément sur ∆ s'il existe f ∈
F(∆, K) (appelée limite uniforme de la suite (fn )) telle que :
(∀ε > 0); (∀N ∈ N) (∃x ∈ ∆) (∀n ≥ N ); |fn (x) − f (x)| ≤ ε
Illustration
6
f (x) + ε
f (x)
fn (x)
f (x) − ε
-
Remarques (Importantes)
1. Remarquons qu'on passe de (1) à (2) en déplaçant (∀x ∈ ∆). La convergence uniforme
entraîne donc la convergence simple (la réciproque est fausse).
2. La convergence uniforme de (fn ) vers f peut s'écrire aussi :
lim
n→+∞
sup |fn (x) − f (x)|
=0
x∈∆
Critère de Cauchy de convergence uniforme
Comme K est complet on a alors : (fn ) converge uniformément vers f sur ∆ si et
seulement si :
∀ε > 0; ∃N ∈ N; ∀x ∈ ∆; ∀n ≥ N ; ∀p ∈ N∗ ; |fn+p (x) − fn (x)| ≤ ε
Exemples
Reprenons la suite fn (x) =
nx2
.
1+nx2
1. Nous avons vu que (fn ) converge simplement vers f : x 7−→ f (x) =
1 si x 6= 0
. On a
0 si x = 0
de plus la convergence uniforme de (fn ) sur tout l'intervalle [ω, +∞[. En eet :
nx2
1
|fn (x) − f (x)| = − 1 =
2
1 + nx
1 + nx2
I.Elmahi
2
Année 2007-2008
ENSA1
Analyse II
On veut que :
Suites et Séries de Fonctions
"
#
lim
n→+∞
|fn (x) − f (x)| = 0
sup
x∈[ω, +∞[
1
−−−−−→ 0
1 + nω 2 n→+∞
2. A-t-on convergence uniforme sur [0, ω[ ?
=
1
= 1 6= 0
2
ω[ 1 + nx
cn = sup |fn (x) − f (x)| = sup
x∈[0, ω[
x∈[0,
Donc (fn ) ne converge pas uniformément vers f sur [0, ω[.
2 Théorèmes fondamentaux sur les suites de fonctions
Les théorèmes que nous allons établir donnent une réponse au problème suivant :
Problème
Etant donné une suite de fonctions (fn ) dont on connaît les propriétés : (fn ) continue
ou dérivable, pour tout n, peut-on armer que la fonction limite f de (fn ) est elle
même continue ou dérivable ?
2.1 Continuité
Théorème
Soit(fn ) une suite de fonctions continues de [a, b] dans K converge uniformément sur
[a, b]. Alors la limite f est continue sur [a, b].
Remarque
Ce théorème se traduit en disant que "la limite uniforme d'une suite de fonctions continue
est continue".
Preuve
Soit (fn ) une suite de fonctions qui converge uniformément sur [a, b] vers f . Alors :
(1) ∀ε > 0; ∃N ∈ N; ∀n ≥ N ; ∀x ∈ [a, b]; |fn (x) − f (x)| ≤
ε
3
Considérons la fonction fN : x 7−→ fN (x). On a fN est continue sur [a, b]. Donc : ∀x0 ∈ [a, b] xé
on a :
ε
(2) ∀ε > 0; ∃η > 0; |x − x0 | < η ⇒ |fN (x) − fN (x0 )| <
3
(Pour montrer la continuité de f , il faut montrer que |f (x) − f (x0 )| < ε). On a :
|f (x) − f (x0 )| ≤ |f (x) − fN (x)| + |fN (x) − fN (x0 )| + |fN (x0 ) − f (x0 )|
Or d'après (1) on a : |fN (x) − f (x)| < 3ε et |fN (x0 ) − f (x0 )| < 3ε .
D'après (2) on a : |fN (x) − fN (x0 )| < 3ε .
Par conséquent on a :
ε ε ε
+ + =ε
3 3 3
Donc f est continue en tout point x0 de [a, b]. f est donc continue sur [a, b].
∀ε > 0; ∃η > 0; |x − x0 | < η ⇒ |f (x) − f (x0 )| <
I.Elmahi
3
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
Remarque (Importante)
• Attention, la convergence simple de la suite (fn ) vers f n'implique pas nécessairement que
f : [0, 1] −→ R
f est continue. Par exemple, prenons l'intervalle [0, 1] et n
. On a :
x
7−→ fn (x) = xn
∀x ∈ [0, 1[;
lim fn (x) = lim xn = 0
n→+∞
n→+∞
x = 1 ; fn (1) = 1 donc limn→+∞ fn (1) = 1.
Donc (fn ) converge simplement dans [0, 1] vers la fonction : f : x 7−→ f (x) =
On voit bien que f n'est pas continue dans [0, 1] (elle n'est pas continue en 1).
D'ailleur, la convergence de (fn ) vers f n'est pas uniforme ; en eet :
0 si x 6= 1
.
1 si x = 1
sup |fn (x) − f (x)| = sup |xn − f (x)| = 1
x∈[0,1]
x∈[0,1]
ne tend pas vers 0.
2.2 Intégration
Théorème
Soit (fn ) une suite de fonctions intégrable, convergeant uniformément vers f sur [a, b],
alors :
1. f est intégrable sur [a, b].
2.
Z
Z
Z
b
lim
n→+∞ a
3. La suite gn (x) =
Rb
a
b
fn (x)dx =
b
lim fn (x)dx =
a n→+∞
f (x)dx
a
fn (t)dt converge uniformément sur [a, b] vers
Rx
a
f (t)dt.
Remarque
Ce théorème montre qu'on peut échanger l'intégration et le passage à la limite, lorsque la
suite de fonctions intégrables (fn ) convergent uniformément vers f .
Preuve
On va montrer 3., les propriétés 1. et 2. sont laissées en exercice.
comme la suite (fn ) converge uniformément vers f sur [a, b], alors :
∀ε > 0; ∃N ∈ N; ∀n ≥ N, ∀x ∈ [a, b], |fn (x) − f (x)| <
Comme |fn (x) − f (x)| et
ε
(b−a)
Z
sont positifs, alors :
b
Z
b
|fn (x) − f (x)|dt <
a
Or on a :
ε
(b − a)
a
Z x
Z
(fn (t) − f (t))dt ≤
x
ε
=ε
(b − a)
Z
b
|fn (t) − f (t)|dx ≤
|fn (t) − f (t)|dt
a
a
a
Z x
Z x
Donc ∀ε > 0; ∃N ∈ N; ∀x ∈ [a, b]; fn (t)dt −
f (t)dt < ε
a
Donc la suite de fonctions gn (x) =
I.Elmahi
Rb
a
a
fn (x)dx converge uniformément vers g(x) =
4
Rx
a
f (x)dx.
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
Exemple
Soit I = [0, π] et (fn ) la suite de fonctions dénie sur I par :
∀n ∈ N; fn (x) = sinn (x)(1 − sinn (x))
• Il est clair que ∀n ∈ N; fn est continue sur [0, π] donc intégrable.
• Convergence uniforme
∀x ∈ [0, π] on a :
Si x 6= π2 : On a 0 ≤ sin x < 1 donc 0 ≤ sinn x < 1.
D'où : limn→+∞ sinn (x) = 0 et limn→+∞ fn (x) = 0.
Si x =
π
2
:
π
π
π
fn ( ) = sinn ( )(1 − sinn ( )) = 0
2
2
2
Donc la suite (fn ) converge simplement vers la fonction nulle :
De plus, si l'on pose u = sin x, on a :
f : I −→ R
x 7−→ f (x) = 0
sup |fn (x) − f (x)| = sup sinn (x)(1 − sinn (x))
x∈[0,π]
x∈[0,π]
On a
Donc
sup u(1 − u) =
x∈[0,π]
sup |fn (x) − f (x)| =
x∈[0,π]
1
4
1
−−−−−→ 0
4n n→+∞
D'où la suite (fn ) converge uniformément vers la fonction nulle f (x) = 0. En appliquant le
théorème précédent :
Z
lim
n→+∞ 0
π
sinn (x)(1 − sinn (x))dx =
Z
0
π
lim sinn (x)(1 − sinn (x))dx =
n→+∞
Z
π
0dx = 0
0
2.3 Dérivation
Théorème
Soit (fn ) une suite de fonctions sur [a, b] telle que :
1. (fn ) est de classe C 1 sur [a, b].
2. ∃x0 ∈ [a, b] / la suite fn (x0 ) converge (limn→+∞ fn (x0 ) = l).
3. La suite (fn0 ) converge uniformément sur [a, b] vers une fonction g .
Alors
1. La suite (fn ) converge uniformément sur [a, b] vers la fonction f dénie par :
Z
x
f (x) = l +
g(t)dt
x0
2. f est dérivable sur [a, b] et l'on a : f 0 = g
I.Elmahi
5
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
Remarque (f 0 = g)
Ce résultat s'écrit aussi :
0
= lim fn0 (x)
lim fn (x)
n→+∞
n→+∞
i,e qu'on peut échanger la dérivation et le passage à la limite.
Preuve
On a la suite (fn0 ) de fonctions converge uniformément vers g . De plus comme (fnR0 ) est intégrable car fn est de classe C 1R, d'après le théorème d'intégration, la suite de fonctions xx0 fn0 (x)dt
converge uniformément vers xx0 g(x)dx.
Or on
R x a limn→+∞ fn (x0 ) = l. On montre que la suite (fn ) converge uniformément sur [a, b] vers
l + x0 g(x)dx.
En eet : ∀x ∈ [a, b] ;
Z
fn (x) − l +
x
x0
Z
g(t)dt = x
fn0 (t)dt
Z
+ fn (x0 ) − l −
x0
Z
≤ |fn (x0 ) − l| + x
x0
g(t)dt
Z x
x
0
fn (t)dt −
g(t)dt
x0
x0
Lorsque n → +∞, les deux modules du second membre tendent chacune vers 0. Donc le
R premier
membre tend aussi vers 0. La suite (fn ) converge donc uniformément vers f (x) = l + xx0 g(t)dt.
Il est clair aussi que f est dérivable sur [a, b] et on a : f 0 (x) = g(x)∀x ∈ [a, b].
I.Elmahi
6
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
Deuxième partie
Séries de fonctions
1 Dénition
Soit Un (x) une suite de fonctions dénies d'un ensemble ∆ vers un corps K.
Un : ∆ −→ K
. A partir de cette suite de fonctions, on peut dénir
x 7−→ Un (x)
une nouvelle suite de fonctions Sn (x) par :
∀n ∈ N
S0 (x) = U0 (x)
S1 (x) = U0 (x) + U1 (x)
..
.
Sn (x) = U0 (x) + · · · + Un (x) =
Pn
k=0 Uk (x)
On apelle série de fonctions
la suite des couples de fonctions (Un (x), Sn (x)). On note
P
en général la série par Un (x).
Sn (x) est la somme des suites partielles.
Un (x) est le terme général de la suite.
2 Convergence simple, convergence uniforme de séries de fonctions
Dénition 1
On dit que la série de fonctions Un (x) converge simplement sur ∆ si la suite des
sommes partielles (Sn (x)) converge simplment sur ∆. Si on appelle S(x) la limite
simple de Sn (x), alors on a :
P
∀x ∈ ∆; ∀ε > 0; ∃N ∈ N; ∀n ≥ N ;
|Sn (x) − S(x)| < ε
P
S(x) = limn→+∞ Sn (x) est appelée somme de la série
Un (x)
Dénition 2
On dit que la série de fonctions Un (x) converge uniformément sur ∆ si la suite des
sommes partielles (Sn (x)) converge uniformément sur ∆. Autrement dit :
P
∀ε > 0; ∃N ∈ N; ∀n ≥ N ; ∀x ∈ ∆;
|Sn (x) − S(x)| < ε
La convergence uniforme sur ∆ s'écrit aussi :
lim sup |Sn (x) − S(x)| = 0
n→+∞ x∈∆
2.1 Critère de Cauchy de convergence uniforme dans un espace complet
La série de fonctions
Un (x) converge uniformément sur ∆ si et seulement si :
n+p
X
∗
∀ε > 0; ∃N ∈ N; ∀n ≥ N ; ∀p ∈ N ; ∀x ∈ ∆; Uk (x) < ε
P
k=n+1
I.Elmahi
7
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
Exemple
Considérons la série de fonctions
P
Un (x) dénie sur R par :
∀n ∈ N;
• Convergence simple de
P
Un (x) =
x
(1 + |x|)n
Un (x) sur R :
La suite des sommes partielles :
Pn
x
Sn (x) =
k=0 (1+|x|)k
x
x
x
Sn (x) = x + 1+|x|
+ (1+|x|)
2 + · · · + (1+|x|)n
2
n 1
1
1
= x 1 + 1+|x| + 1+|x| + · · · + 1+|x|
Si x = 0, alors ∀n ∈ N;
Si x 6= 0,
Un (0) = 0. Donc Sn (0) = 0. D'où limn→+∞ Sn (0) = 0.
"
Sn (x) = x
Or 0 <
1
1+|x|
< 1 donc limn→+∞
1
1+|x|
n+1
lim Sn (x) =
n→+∞
La série de fonctions
P
1
)n+1
1 − ( 1+|x|
1−
#
1
1+|x|
= 0. D'où :
x
1−
=
1
1+|x|
x(1 + |x|)
|x|
Un (x) converge simplement sur R vers sa somme S(x) dénie par :
S : R −→ R
(
x
7−→
0
x(1+|x|)
|x|
si x = 0
si x =
6 0
• Convergence uniforme sur R :
n+1 !
1
1− 1+|x|
supx∈R |Sn (x) − S(x)| = supx∈R∗ x
−
1
1− 1+|x|
−x 1 n+1 1+|x|
= supx∈R∗ 1−
1
1+|x|
n
1
= supx∈R∗ 1+|x|
= 1 6= 0
Il n'ya pas de convergence uniforme sur R de la série
y'a convergence uniforme sur [a, +∞[; a 6= 0.
P
x
1
1− 1+|x| Un (x), par contre on peut montrer qu'il
2.2 Convergence normale
On dit qu'une
P série de fonctions converge normalement sut ∆ s'il existe une série
numérique Vn convergente telle que l'on ait :
∀x ∈ ∆;
I.Elmahi
|Un (x)| ≤ Vn
8
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
Exemples
1. ∆ = [0, 1];
Un (x) =
x
.
(n+1)2
On a :
x
1
≤
∀x ∈ ∆; |Un (x)| = 2
(n + 1)
(n + 1)2
P 1 P
Or la série numérique
converge. Donc Un (x) converge normalement sur ∆.
(n+1)2
2. ∆ = R;
Un (x) =
sin(nx)
.
n2
sin(nx) 1
n2 ≤ n2
∀x ∈ ∆;
converge (Riemann). Donc Un (x) converge normalement.
3. ∆ = R+ ; Un (x) = xn e−nx . Calculons supx∈R+ |Un (x)| = supx∈R+ xn e−nx .
Posons f (x) = xn e−nx .
Or
1
n2
P
∀x ∈ R+ ;
f 0 (x) = nxn−1 e−nx − ne−nx xn = xn−1 ne−nx (1 − x)
f 0 (x) = 0
x = 1 ou x = 0
⇐⇒
x
0
f 0 (x)
f
P
+∞
+
−
−n
% e
&
√
n
1
−n = V . Or
supx∈R
e−n converge car
n
P+ |Un (x)| = e
D'où Un (x) converge normalement.
e−n = e−1 < 1 d'après Cauchy.
2.3 Condition susante de convergence uniforme
Théorème (important)
Si
P
Un (x) converge normalement sur ∆, alors elle converge uniformément sur ∆.
Preuve
Vn série numérique
convergente.
Utilisons le critère de Cauchy de convergence uniforme dans un espace complet :
P
Un (x) converge normalement sur ∆ : ∀x ∈ ∆;
|Un (x)| ≤ Vn avec
P
P
n+p
k=n+1 Uk (x) = |Un+1 (x) + · · · + Un+p (x)|
≤ |Un+1 | + · · · + |Un+p (x)|
≤ Vn+1 + Vn+2 + · · · + Vn+p
Comme
Un converge, alors
P elle vérie
le critère de Cauchy dans un espace complet. C'est à
P
n+p n+p
dire n+1 Vk < ε. D'où n+1 Uk (x) < ε.
P
Exemple
Un (x) =
∀x ∈ R;
et
P
1
n3
sin(nx)
n3 + x2
|Un (x)| ≤
∆=R
n3
1
1
≤ 3
2
+x
n
converge normalement donc il y'a convergence uniforme.
I.Elmahi
9
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
3 Théorèmes fondamentaux sur les séries de fonctions
3.1 Théorème de continuité
Soit
Un (x) une série de fonctions convergeant uniformément sur ∆ vers sa somme
S(x) et telle que ∀n ∈ N; Un (x) est continue sur ∆.
Alors S(x) est continue sur ∆.
P
Preuve
Un (x) converge sur ∆ vers S(x) ⇐⇒ la suite de fonctions Sn (x) converge uniformément
sur ∆ vers S(x). De plus, comme ∀n; Un (x) est continue sur ∆, alors ∀n; Sn (x) est continue sur
∆ vers S(x).
D'après le théorème de continuité des suites de fonctions, S(x) est continue sur ∆.
P
Remarque
Le théorème de continuité a comme résultat :
lim
x→x0
+∞
X
!
Un (x)
=
n=0
+∞ X
lim Un (x)
x→x0
n=0
3.2 Théorème d'intégration
Soit Un (x) une série de fonctions convergeant uniformément sur [a, b] vers S(x) et
telle que ∀n ∈ N; Un (x) est intégrable sur [a, b]. Alors :
1. S(x) est aussi intégrable sur [a, b].
2.
!
Z
Z
Z
P
+∞
X
b
b
Un (t)dt
=
a
n=0
a
+∞
X
b
Un (t)dt dt =
3. La série de fonctions
Vn (x) avec Vn (x) =
R
sur [a, b] vers ax S(t)dt.
P
S(t)dt
a
n=0
Rx
a
Un (t)dt converge uniformément
Preuve
(Sn ) converge uniformément vers S . donc ∀n; Sn est intégrable. D'où :
1. S est intégrable.
2.
Z
lim
n→+∞ a
I.Elmahi
b
Z
Sn (t)dt =
b
S(t)dt =
a
Z bX
n
a k=0
10
Uk (t)dt =
+∞ Z
X
b
Un (t)
n=0 a
Année 2007-2008
ENSA1
Analyse II
Suites et Séries de Fonctions
3.3 Théorème de dérivation
Soit Un (x) une série de fonctions dénie sur [a, b] et telle que :
1. ∀n ∈ N; Un (x) ∈ C 1 ([a, b]).
P
2. ∃x0 ∈ [a, b] tel que la série numérique Un (x0 ) converge.
P
3. La série Un0 (x) converge uniformément sur ∆
Alors :
P
1. Un (x) converge uniformément sur ∆.
2. S(x) est de classe C 1 sur [a, b] et on a :
P
S 0 (x) =
+∞
X
!0
Un (x)
=
n=0
+∞
X
Un0 (x)
n=0
Preuve
Utiliser le théorème de dérivation des suites de fonctions.
Variante du théorème de dérivation
Soit Un (x) une série de fonctions dénie sur [a, b] et telle que :
1. ∀n ∈ N; Un (x) ∈ C 1 ([a, b]).
P
2. ∃x0 ∈ [a, b] tel que la série numérique Un (x0 ) converge.
P
3. La série Un0 (x) converge uniformément sur tout ségment [c, d] de [a, b].
Alors :
P
1. Un (x) converge uniformément sur tout ségment [c, d] de [a, b].
2. S(x) est de classe C 1 sur [a, b] et on a :
P
0
S (x) =
+∞
X
!0
Un (x)
n=0
=
+∞
X
Un0 (x)
n=0
I.Elmahi
11
Année 2007-2008