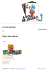T.Tomala. HEC Majeure Economie Examen corrigé de théorie des

T.Tomala. HEC Majeure Economie
Examen corrigé de théorie des jeux. 2h00.
Exercice 1. Soit le jeu à deux joueurs suivant dans lequel le joueur 1
choisit la ligne et le joueur 2 la colonne.

(3, 3)
 (4, 1)
G=
 (2, 9)
(2, 11)
(1, 4)
(0, 0)
(0, 9)
(0, 3)

(6, 2) (1, 2)
(6, 0) (3, 0) 

(6, 8) (5, 6) 
(5, 7) (10, 10)
(1) Ce jeu est-il résoluble par élimiation itérée de stratégies strictement dominées ?
(2) Déterminer tous les équilibres de Nash (purs et mixtes) de ce
jeu.
(3) Les équilibres de Nash sont-ils Pareto-optimaux dans ce jeu?
Est-ce toujours le cas?
Solutions: Après élimination itérée de stratégies strictement dominées,
il reste le jeu:
(3, 3) (1, 4)
(4, 1) (0, 0)
Ce jeu a deux équilibres purs: (B, G) et (H, D). Il n’y a pas d’équilibre
ou un joueur joue en mixte et l’autre en pur: dès que 1 joue en pur, 2
préfère jouer en pur également. On cherche les équilibres ou les deux
jouent en mixtes. Soient (x, 1 − x) et (y, 1 − y) les stratégies mixtes
d’équilibre avec 0 < x < 1 et 0 < y < 1. Le theoreme d’indifférence
donne g1 (H, y) = g1 (B, y). Donc, 3y + (1 − y) = 4y, soit y = 1/2. De
la meme facon, x = 1/2.
Les deux equilibres purs sont Pareto-optimaux dans ce jeu. On peut
vérifier que l’équilibre mixte donne les paiements (2,2) qui sont dominés
par (3,3). Le dilemme du prisonnier est un exemple célèbre où le seul
équilibre est pareto-dominé.
Exercice 2. Alice et Bob ont le même ordinateur portable. Malheureusement, les deux ordinateurs ont été volés. L’assurance veut
leur rembourser au juste prix et propose la règle suivante. Alice et
Bob doivent annoncer chacun la valeur estimée de leur ordinateur. Les
choix sont faits simultanéments. Soit x la valeur annoncée par Alice et
y la valeur annoncée par Bob.
• Si x = y alors chacun reçoit cette somme.
• Si x < y, alors Alice reçoit x + 2 et Bob reçoit x − 2.
• Si x > y, alors Alice reçoit y − 2 et Bob reçoit y + 2.
On suppose que les valeurs annoncées doivent être choisies parmi les
nombres entiers compris entre 2 et 6.
1
2
(1) Ecrire la matrice de ce jeu.
(2) Montrer que (2, 2) est le seul équilibre de Nash (pur ou mixte).
Indications: Le montrer d’abord en pur. Montrer ensuite que
la stratégie 6 est forcément jouée avec probabilité zéro dans un
équilibre mixte. Conclure en poursuivant ce raisonnement.
(3) On suppose maintenant qu’Alice joue avant Bob : Alice choisit
x, l’annonce à Bob, qui choisit alors y.
Résoudre ce jeu par backward induction et comparer avec
l’équilibre de Nash du jeu simultané.
Solutions. La matrice du jeu est la suivante:
2
3
2 2, 2 4, 0
3 0,4 3,3
4 0,4 1,5
5 0,4 1,5
6 0,4 1,5
4
4,0
5,1
4,4
2,6
2,6
5
4,0
5,1
6,2
5,5
3,7
6
4,0
5,1
6,2
7,3
6,6
En cherchant les meilleures réponses, on voit facilement que (2,2)
est le seul équilibre pur. La stratégie 6 est faiblement dominée par 5,
ce qui ne suffit pas pour dire qu’elle n’est pas jouée à l’équilibre.
Supposons que 6 soit jouée avec probabilité non nulle. Le théorème
d’indifférence dit alors qu’elle est meilleure réponse contre la stratégie
du joueur 2. Or on voit facilement que 6 n’est jamais meilleure réponse!
: il vaut toujours mieux jouer 2 ou 5. En fait, pour que 6 soit préférable
(au sens large) à 5, il faut que le joueur 2 ne joue que 2,3 ou 4 avec
proba>0. Mais dans ce cas, jouer 2 assure un paiement plus grand que
jouer 6.
La stratégie 6 n’est donc présente dans aucun équilibre. On peut
donc l’éliminer pour trouver les équilibres. On constate alors que, dans
le jeu restant, on peut éliminer 5 par le meme argument (5 n’est jamais
meilleure réponse dans le jeu restant). En itérant ce raisonnement, seul
2 reste comme stratégie possible.
Si Alice joue avant Bob, elle anticipe que celui-ci jouera une meilleure
réponse BR(a) si elle joue a. Comme BR(2) = 2, BR(3) = 2,
BR(4) = 3, BR(5) = 4 et BR(6) = 5, Alice jouera 6, et les paiements
sont (3, 7). Cette situation est préférable pour les deux joueurs.
Exercice 3. Deux firmes i = 1, 2 se font concurrence sur un même
marché. Chaque firme i doit choisir sa quantité de production qi ∈ R+ ,
les choix étant simultanés. Si la quantité totale produite est Q = q1 +q2 ,
le prix de marché du bien est fixé à P (Q) = max(1 − Q, 0).
• La firme 1 qui produit la quantité q1 doit payer un coût de
production C1 (q1 ) = q12 .
3
• La firme 2 qui produit la quantité q2 doit payer un coût de
production C2 (q2 ) = cq22 avec c > 0.
• Le but de chaque firme est de maximiser son bénéfice net,
bénéfice = quantité × prix de marché − coût.
(1) Ecrire le jeu sous forme stratégique associé (ensembles de stratégies,
fonctions de paiements).
(2) Montrer que pour toute stratégie q2 du joueur 2, le joueur 1 a
une unique meilleure réponse b1 (q2 ) qui vaut:
1 − q2
b1 (q2 ) = max{
, 0}.
4
(3) Montrer que pour toute stratégie q1 du joueur 1, le joueur 2 a
une unique meilleure réponse b2 (q1 ) qui vaut:
1 − q1
b2 (q1 ) = max{
, 0}.
2(c + 1)
(4) Déterminer les équilibres de Nash de ce jeu (en justifiant la
réponse). Calculer le prix d’équilibre en fonction du paramètre
c.
(5) Comparer le prix limite quand c tend vers l’infini avec la situation où le joueur 1 est en situation de monopole sur le marché.
Solutions. S1 = S2 = R+ . On suppose d’abord que q1 et q2 sont
inférieurs à 1.
g1 (q1 , q2 ) = (1−q1 −q2 )q1 −q12 = (1−2q1 −q2 )q1 = 2((1−q2 )/2−q1 )q1 .
g2 (q1 , q2 ) = (1 − q1 − q2 )q2 − cq22 = (1 − q1 − (1 + c)q2 )q2
= (1 + c)((1 − q1 )/(1 + c) − q2 )q2 .
Ce sont deux fonctions quadratiques (paraboles), le sommet est au
milieu des deux points d’annulation. D’ou b1 (q2 ) = (1 − q2 )/4 et
1−q1
b2 (q1 ) = 2(c+1)
.
On vérifie facilement que si q2 > 1, le prix est nul. Le profit est donc
≤ 0 et le q1 optimal est 0. Idem si q1 > 1.
L’équilibre est donc la solution du systéme:
q1 = (1 − q2 )/4
1−q1
q2 = 2(c+1)
On trouve q1 = (2c+1)/(8c+7) et q2 = 3/(8c+7). Le prix d’équilibre
est p = 1 − q1 − q2 = (6c + 3)/(8c + 7).
Lorsque c tend vers +∞, ce prix tend vers 34 qui est le prix de monopole pour le joueur 1. q1 tend vers 1/4 et q2 tend vers 0. Le cout de
production du joueur 2 est tellement élevé qu’il ”sort” du marché.