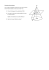Volume et surface d`une calotte sphérique

Volume et aire d’une calotte sphérique L’objectif de cette note est d’abord de prouver deux formules classiques de calcul de volume et d’aire qui permettront ensuite d’obtenir le volume et l’aire d’une calotte sphérique, sans utiliser le calcul intégral. En nous basant sur des idées d’Archimède (IIIe s. avant J.-­‐C.) et de Cavalieri (XVIIe s.) démontrons que le volume V d’une boule de rayon r est donné par la formule V = 4 ! r 3 . 3
Pour cela considérons une demi-­‐boule de rayon OA’ :=r, inscrite dans un cylindre contenant un cône droit de même base que le cylindre (cf. le croquis ci-­‐dessous extrait de Référentiel de mathématiques chez de Boeck). Pour parvenir à nos fins appliquons ce que l’on appelle aujourd’hui le principe de Cavalieri qui peut se résumer à : « Si les sections quelconques de deux solides, parallèles à un plan fixé produisent des aires identiques alors le volume des solides est pareil. » Dans ce cas l’on voit aisément que : aire du disque de rayon AB + aire du disque de rayon AC = aire du disque rayon A’B’ car AB = OA et CO =A’B’ et donc par le théorème de Pythagore OA2+ CA2 = CO2. Ainsi, par le principe de Cavalieri le volume du cône + volume de la demi-­‐boule = volume du 1
1
4
cylindre c’est-­‐à-­‐dire ! r 3 + V boule = ! r 3 d’où V boule = ! r 3 . 3
2
3
Corollaire. L’aire S d’une sphère de rayon r est donnée la formule S = 4! r 2 . Imaginons que du centre O de la boule l’on projette un milliard de rayons (laser) de manière (quasi) homogène dans toutes les directions. Les intersections avec la boule définissent un milliard de sommets. Relions chaque sommet à ses sommets voisins de telle sorte à ce que la sphère soit tapissée (décomposée) en des milliards de petits triangles (sphériques) d’aire !S
(proche de 0). Il est raisonnable d’estimer alors que le volume de chaque ‘pyramide’ de centre O et de base d’aire !S soit !S " r ÷ 3 . D’où, la somme des volumes de chaque ’pyramide’ = volume total de la boule, que l’on note (avec le symbole ‘sigma’ qui signifie ‘somme’) 1
1
1
4
# 3 ! "S ! r = 3 ! r ! # "S = 3 ! r ! S = 3 ! r 3 On conclut en multipliant la dernière égalité par 3 et en la divisant par r. Exercice. En vous basant sur les résultats précédents prouvez que le volume d’une calotte !h2
3r ! h . sphérique de hauteur h :=AA’ est V calotte =
3
Considérez à présent le « cône de glace » OCA’ composé d’un cône OCA et d’une calotte ACA’. Appliquez le même type de raisonnement que ci-­‐dessus pour démontrer que l’aire de la calotte est donnée par la formule : S calotte = 2! rh . (
)