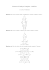Module complémentaire I de Mathématiques Département de Génie

Transcription

Module complémentaire I de Mathématiques
Département de Génie Electrique et Informatique Industrielle
IUT du Havre
Gisella Croce
Table des matières
1 Avant-propos
2
2 Opérateurs différentiels
2.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
3
4
3 Intégrales curvilignes
3.1 Définition et propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
5
6
4 Champs qui dérivent d’un potentiel
8
4.1 Définition et résultats théoriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
4.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
5 Théorème de la divergence dans le plan
11
5.1 Définition et énoncé du théorème . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
5.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
6 Intégrales de surface
13
6.1 Définitions et propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
6.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
7 Théorème de Stokes
14
7.1 Enoncé du théorème . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
7.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
8 Appendice 1 : exemples de courbes et surfaces
15
8.0.1 Exemples de courbes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
8.0.2 Exemples de surfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
9 Appendice 2 : exemple d’interrogation écrite et exemple de DS
18
9.1 Exemple d’interrogation écrite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
9.2 Exemple de DS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
10 Corrigés
10.1 Corrigé
10.2 Corrigé
10.3 Corrigé
10.4 Corrigé
10.5 Corrigé
des
des
des
des
des
exercices
exercices
exercices
exercices
exercices
du
du
du
du
du
chapitre
chapitre
chapitre
chapitre
chapitre
Intégrales curvilignes . . . . . . . . . . .
Champs qui dérivent d’un potentiel . . .
Théorème de la divergence dans le plan
Intégrales de surface . . . . . . . . . . .
Théorème de Stokes . . . . . . . . . . .
11 Retrouver ce cours sur le web : EUREKA
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
19
20
24
26
28
29
32
1
Chapitre 1
Avant-propos
Ce polycopié a été élaboré à partir du livre B.Dacorogna et C.Tanteri Analyse avancée pour ingénieurs, Presses
polytechniques et universitaires romandes, 2002. Les figures ont été réalisées avec le logiciel Winfig.
Même s’il a été contrôlé plusieurs fois, ce polycopié pourrait contenir des imprécisions. Merci aux étudiants qui
voudront me signaler les erreurs éventuelles.
Gisella Croce
2
Chapitre 2
Opérateurs différentiels
2.1
Définitions
Soit Ω un domaine de Rn ; on notera x = (x1 , x2 , .., xn ) un point de Ω. Les deux définitions suivantes concernent
des fonctions f : Ω → R.
Définition 2.1.1 (Gradient) Si f ∈ C 1 (Ω), on définit pour x ∈ Ω le gradient de f comme
∂f
∂f ∂f
∈ Rn .
,
, ...,
∇f (x) =
∂x1 ∂x2
∂xn
Exemple 2.1.2 Si f (x1 , x2 ) = x1 x22 alors ∇f = (x22 , 2 x1 x2 ).
Définition 2.1.3 (Laplacien) Si f ∈ C 2 (Ω), on définit pour x ∈ Ω le laplacien de f comme
∆f (x) =
n
X
∂2f
∂x2i
i=1
=
∂2f
∂2f
∂2f
∈ R.
+
+ .. +
2
2
∂x1
∂x2
∂x2n
Exemple 2.1.4 Il est facile de montrer que f (x1 , x2 ) = x1 x22 possède ∆f = 0.
Nous allons maintenant considérer des champs vectoriels, c’est-à-dire des applications
F :
Ω
→ Rn
(x1 , ..xn ) → F (x) = (F1 (x1 , ..xn ), F2 (x1 , ..xn ), ..Fn (x1 , ..xn )) = (F1 (x), F2 (x), .., Fn (x)) .
A noter que F (x) est un vecteur.
On peut imaginer un champ vectoriel de la manière suivante : pour chaque point x ∈ Ω on trace une flèche dont
l’origine est x et la direction est donnée par F (x).
Définition 2.1.5 (Divergence) Soit F (x) = (F1 (x), F2 (x), .., Fn (x)) ∈ C 1 (Ω; Rn ). On définit pour x ∈ Ω la
divergence de F comme
n
X
∂F1
∂F2
∂Fn
∂Fi
=
+
+ ..
∈ R.
div F (x) =
∂x
∂x
∂x
∂xn
i
1
2
i=1
Exercice 2.1.6 Soit F (x1 , x2 ) = (x1 + x32 , x1 cos(x1 + x2 )). Alors div F = 1 − x1 sin(x1 + x2 ).
Définition 2.1.7 (Rotationnel)
1. Soit F : Ω ⊂ R2 → R2 ∈ C 1 (Ω; R2 ). On définit pour x ∈ Ω le rotationnel de F comme
∂
∂
∂F1
∂F2
∂x
∂x
1
2
−
= dét
rot F (x) =
∈ R.
F1
F2
∂x1
∂x2
3
2. Soit F : Ω ⊂ R3 → R3 ∈ C 1 (Ω; R3 ). On définit pour x ∈ Ω le rotationnel de F comme


e1
e2
e3
∂
∂
∂
.
rotF (x) = dét  ∂x
∂x2
∂x3
1
F1
F2
F3
Exemple 2.1.8 Soit F (x, y, z) = (x2 , z, ln(z + x)). Alors


e1 e2
e3
∂
∂
∂
 = (−1, −(z + x)−1 , 0) .
rotF (x) = dét  ∂x
∂y
∂z
2
x
z ln(z + x)
Remarque 2.1.9 En R3 rotF ⊥ F .
2.2
Exercices
Exercice 2.2.1 Soit F (x, y, z) = y 2 sin(xz), ey cos(x2 + z), log(2 + cos(xy)) = (f1 , f2 , f3 ).
Calculer :
a) grad f1 , grad f2 , grad f3
b) div F
c) rot F.
Exercice 2.2.2 Si f : R3 → R est C 1 (R3 ) et F : R3 → R3 est C 1 (R3 ; R3 ),
alors quelles sont parmi les expressions suivantes celles qui ont un sens ?
i) grad f
v) div (f F )
ix) rot div F.
ii) f grad f
vi) rot (f F )
iii) < F ; grad f >
vii) rot f
iv) div f
viii) f rot F
Exercice 2.2.3 Montrer que :
soient f ∈ C 1 (Ω) et g ∈ C 2 (Ω) ; alors
div(f grad g) = f ∆g + grad f grad g;
si f, g ∈ C 1 (Ω) alors
grad(f g) = f grad g + ggrad f.
4
Chapitre 3
Intégrales curvilignes
3.1
Définition et propriétés
Définition 3.1.1 Soit γ : [a, b] → Rn une courbe simple régulière. On notera
γ(t) = (γ1 (t), γ2 (t), .., γn (t))
γ ′ (t) = (γ1′ (t), γ2′ (t), .., γn′ (t))
et
v
u n
q
uX
||γ ′ (t)|| = t (γi′ (t))2 = (γ1′ (t))2 + (γ2′ (t))2 + ..(γn′ (t))2 .
i=1
1) Soit f : γ → R une fonction continue. L’intégrale de f le long de γ est définie par
Z
f dl =
γ
Z
b
f (γ(t))||γ ′ (t)||dt .
a
2) Soit F = (F1 (x), F2 (x), .., Fn (x)) : Γ → Rn un champ vectoriel continu. L’intégrale de F le long de γ est
définie par
Z
Z b
F (γ(t)) · γ ′ (t) dt .
F · dl =
γ
a
Exemple 3.1.2 Soit γ(t) = (cos t, sin t), avec t ∈ [0, π]. Soit f (x1 , x2 ) = x1 x2 . Alors f (γ(t)) = cos t sin t et
||γ ′ (t)|| = 1; par conséquent
Z
Z π
cos t sin t dt = 0 .
f dl =
γ
0
fonction f
courbe γ
5
Remarque 3.1.3
Z
dl =
Z
b
||γ ′ (t)||dt
a
γ
nous donne la longueur de la courbe γ.
R
Remarque 3.1.4 Soit γ : [a, b] → R2 une courbe simple régulière. Soit f : γ → R une fonction positive. γ f dl
est l’aire de la surface que l’on obtient si on élève, en chaque point (x, y) de la courbe γ un mur grand f (x, y)
(à remarquer que le mur est ondulé !).
Exemple 3.1.5 Soit γ(t) = (t, 1 − t) avec t ∈ [0, 1]. Soit F (x1 , x2 ) = (0, −x1 ). Alors
Z
γ
F · dl =
1
Z
(0, −t) · (1, −1) dt =
0
1
.
2
R
Remarque 3.1.6 D’un point de vue géométrique, γ F · dl consiste à additionner la composante du champ F
R
tangente à la courbe γ. On peut donc dire que γ F · dl est une mesure de combien F est aligné à γ. Si γ est
R
fermée, γ F · dl est une mesure de combien de rotation fait F autour de γ. Pour cette raison cette quantité est
aussi appelée "circuitation".
Remarque 3.1.7 Dans les calculs d’une integrale curviligne on utilise par fois la remarque suivante. Soit γ le
graphe d’une fonction f : [a, b] → R. Si l’on parcoure cette courbe de (b, f (b)) à (a, f (a)) une paramétrisation
est alors (a + b − t, f (a + b − t)) pour t ∈ [a, b].
3.2
Exercices
2
2
Exercice 3.2.1 Soit f (x, y) = x + y . Calculer
Z
f dl dans les cas suivants :
Γ
1. γ = segment entre (0, 0) et (M, 0) ;
2. γ = segment entre (0, 0) et (α, β) ;
3. γ = bord du carré (0, 0), (1, 0), (1, 1), (0, 1).
Exercice 3.2.2 Calculer
Z
Z
Γ
1. f (x, y) = x; γ(t) = (cos t, sin t), 0 ≤ t ≤ 2π ;
√
2. f (x, y) = y ; γ(t) = (t − sin t; 1 − cos t), 0 ≤ t ≤ 2π.
Exercice 3.2.3 Calculer
γ
1. f (x, y) = x; γ(t) = (t, t2 ), 0 ≤ t ≤ a ;
2. f (x, y) = y 2 ; γ(t) = (t, et ), 1 ≤ t ≤ 3 ;
3. f (x, y) =
x
1+y 2 ;
4. f (x, y) =
p
γ(t) = (cos t, sin t), 0 ≤ t ≤
π
2
;
1 − y 2 ; γ(t) = (cos t; sin t), 0 ≤ t ≤ π.
Exercice 3.2.4 Soit f (x, y) = x + 2y. Calculer
Z
f dl si γ est le bord du trapèze (0, 0), (2, 0), (1, 1), (0, 1).
γ
Exercice 3.2.5 Soient F (x, y) = (x + y, −x) et Γ = (x, y) ∈ R2 : y 2 + 4x4 − 4x2 = 0, x ≥ 0 .
1) Montrer que α(t) = (sin t, sin 2t) avec t ∈ [0, π] est une paramétrisation de Γ.
Z
2) Calculer
F · dl.
Γ
Exercice 3.2.6 Soit F (x, y) = xy, y 2 − x . Calculer
Z
Γi
6
F · dl, pour
Γ1 = {(t, t) : t ∈ [0, 1]}
Γ2 = {(t, et ) : t ∈ [0, 1]}
√ 2
Γ3 =
t, t : t ∈ [1, 2] .
Exercice 3.2.7 Soit C le cercle de centre (0, 0) et rayon 1. Soit F (x, y) = (x2 , y+x). Soit γn (t) = (cos(nt), sin(nt)),
t ∈ [0, 2π] avec n ≥ 1. Vérifier que
Z
Z
γn
F · dl = n
γ1
F · dl .
Exercice 3.2.8 Soit T le triangle de sommets (0, 0), (2, 2), (−2, 2). Soit F (x, y) = (x2 + 3, y + x). Calculer
Z
F · ds
∂T
Exercice 3.2.9 Soit C le cercle de centre (0, 0, 3) et rayon 2 qui se trouve sur le plan z = 3. Soit F (x, y, z) =
(x + 3, y + x, z + x). Calculer
Z
∂C
F · ds
Exercice 3.2.10 Soit T le triangle de sommets (0, 0, 1), (2, 2, 1), (−2, 2, 1). Soit F (x, y, z) = (y +z, x, −3z +y).
Calculer
Z
F · ds
∂T
√
Exercice 3.2.11 Soit γ(t) = (t2 , t + 1, t − 2), t ∈ [0, 1]. Soit F (x, y, z) = (y + z − 1, 3x, −3z + y). Calculer
Z
F · ds
γ
Exercice 3.2.12 Soit C = {(x, y, z) ∈ R3 : x2 +y 2 ≤ 1, z = 2, x ≥ 0, y ≥ 0}. Soit F (x, y, z) = (x+3, y+x, z+x).
Calculer
Z
F · ds
∂C
7
Chapitre 4
Champs qui dérivent d’un potentiel
4.1
Définition et résultats théoriques
Définition 4.1.1 Soit F = (F1 (x), F2 (x), ..Fn (x)) un champ vectoriel. On dit que f dérive d’un potentiel sur
Ω s’il existe une fonction f ∈ C 1 (Ω) telle que
∂f
∂f ∂f
,
, ..,
x ∈ Ω.
F (x) = ∇f =
∂x1 ∂x2
∂xn
(la fonction f est appelé potentiel).
Exemple 4.1.2 F (x, y) = (y 2 , 2xy) est égal au gradient de la fonction f (x, y) = xy 2 .
Définition 4.1.3 Un ensemble Ω est convexe si pour tout point A, B ∈ Ω le segment joignant A à B appartient
à Ω.
Exemple 4.1.4 Rn est convexe ; un triangle est convexe ; une étoile n’est pas convexe.
Théorème 4.1.5 Soit F un champ vectoriel de classe C 1 (Ω; Rn ), n = 2, 3.
1) Si F dérive d’un potentiel alors rot F = 0.
2) Si le domaine Ω est convexe et rot F = 0 alors F dérive d’un potentiel.
Théorème 4.1.6 Soit F : Ω → Rn un champ continu. Les affirmations suivantes sont équivalentes :
1. F dérive d’un potentiel sur Ω.
2. Pour toute courbe simple fermée, régulière Γ ⊂ Ω
Z
Γ
F · dl = 0
3. Soient Γ1 , Γ2 ⊂ Ω deux courbes simples fermées, régulières joignant A à B. Alors
Z
Z
F · dl =
F · dl .
Γ1
Γ2
Remarque 4.1.7 (Une application) Considérons un corps de masse m. Sa force poid est F = (0, 0, mg), g
étant l’accélération de gravité. Cette force dérive du potentiel f (x, y, z) = mgz, (z est la hauteur
à laquelle le
Z
corps se trouve). Depuis la physique on sait bien que le travail de cette force, c’est-à-dire
F · dl, ne dépend
γ
pas du chemin, mais seulement du point de départ et du point d’arrivée...c’est exactement ce que le théorème
4.1.6 nous dit.
8
A
B
exemple de domaine non convexe
exemple de domaine convexe
9
4.2
Exercices
Exercice 4.2.1 Soit F (x, y) = (4x3 y 2 , 2x4 y + y). Montrer que F dérive d’un potentiel sur R2 et trouver un
tel potentiel.
Exercice 4.2.2 Soit F (x, y) =
1. Ω1 = {(x, y) ∈ R2 : y > 0}
−
y
x
. Trouver le domaine de définition de F . Soient
,
x2 + y 2 x2 + y 2
2. Ω2 = {(x, y) ∈ R2 : y < 0}
3. Ω3 = R2 \ {(x, y) ∈ R2 : x ≤ 0 , y = 0}
4. Ω4 = R2 \ {(0, 0)}
F dérive-t-il d’un potentiel sur Ωi ? Si oui, trouver tel potentiel, sinon trouver Γ ⊂ Ωi tel que
Z
f · dl 6= 0
Γ
Exercice 4.2.3 Soit F (x, y, z) = (2x sin z, zey , x2 cos z + ey ). Montrer que F dérive d’un potentiel sur R3 et
trouver un tel potentiel.
z
2
2
Exercice 4.2.4 Soit F (x, y, z) = 2xy +
, x + 2yz, y + arctgx . Le champ F dérive-t-il d’un potentiel
1 + x2
sur R3 ? Si oui, trouver ce potentiel.
Exercice 4.2.5 Soient les champs
F (x, y) =
−x
−y
,
(x2 + y 2 )2 (x2 + y 2 )2
G(x, y) =
−xy 2
y3
,
(x2 + y 2 )2 (x2 + y 2 )2
et
et soit Ω = R2 \ {(0, 0)}. Dérivent-ils d’un potentiel sur Ω ? (Si oui, trouver tel potentiel, si non justifier votre
réponse).
Exercice 4.2.6 Démontrer que les champs suivants dérivent d’un potentiel
x + 2y
y
1. F (x, y) =
,
(x + y)2 (x + y)2
!
y
x
,p
2. F (x, y) = p
x2 + y 2
x2 + y 2
3. F (x, y) = 3x2 y − 2y 2 , x3 − 4xy .
Exercice 4.2.7 Soit l’équation différentielle :
f2 (t, u(t)) u′ (t) + f1 (t, u(t)) = 0,
t ∈ R.
(4.1)
i) Soit F (x, y) = (f1 (x, y), f2 (x, y)) un champ vectoriel qui dérive d’un potentiel f sur R2 . Montrer qu’une
solution u = u(t) de (1) sous forme implicite est donnée par :
f (t, u(t)) = constante, ∀t ∈ R.
d
Suggestion : Calculer
f (t, u(t)) .
dt
ii) En déduire une solution de :
u2 (t)u′ (t) + sin t = 0.
u(0) = 3.
10
Chapitre 5
Théorème de la divergence dans le plan
5.1
Définition et énoncé du théorème
On dit que Ω ⊂ R2 est un domaine régulier si son bord est une courbe simple fermée et régulière par morceaux.
On dit que ∂Ω est orienté positivement si le sens de parcours de ∂Ω laisse le domaine à gauche.
Théorème 5.1.1 Soit Ω ⊂ R2 un domaine régulier dont le bord est orienté positivement. Soit ν la normale
unitée externe au bord de Ω. Soit
F = (F1 (x1 , x2 ), F2 (x1 , x2 ))
un champ vectoriel de classe C 1 (Ω; R2 ). Alors
ZZ
ZZ Z
∂F1
∂F2
F · ν dl
divF (x1 , x2 )dx1 dx2 =
+
dx1 dx2 =
∂x1
∂x2
∂Ω
Ω
Remarque 5.1.2
Z
∂Ω
Ω
F · ν dl est appelé flux de F à travers ∂Ω.
2
Quelle est l’utilité du
RR théorème de la divergence ? Si on veut calculer le flux de F à travers une courbe γ en R ,
il suffit de calculer A div F où A est l’aire délimitée par γ.
Remarque 5.1.3
1. Comment on calcule la normale au bord de Ω ? Si γ(t) = (x(t), y(t)), t ∈ [a, b] est une
paramétrisation du bord de Ω, la normale ν est un vecteur orthogonal à γ ′ (t) = (x′ (t), y ′ (t)). Par conséquent
ν(t) = (−y ′ (t), x′ (t)) ou ν(t) = (y ′ (t), −x′ (t)). Pour que la formule de la divergence soit vérifiée, il faut
choisir, entre (−y ′ (t), x′ (t)) ou (y ′ (t), −x′ (t)) pour que la normale soit externe !
2. F · ν est une fonction et pas un champ vectoriel !
Exemple 5.1.4 Soit Ω leRR
triangle de sommets (−1, 0), (0, 1), (1, 0). Soit F (x, y) = (x, y + 2). La divergence de
F vaut 2 ; par conséquent
divF = 2. D’ailleurs ∂Ω est composé par
Ω
1. γ1 (t) = (t, 0) avec t ∈ [−1, 1] ;
2. γ2 (t) = (1 − t, t) avec t ∈ [0, 1] ;
3. γ3 (t) = (−t, 1 − t) avec t ∈ [0, 1] ;
donc
Z
∂Ω
F · ν dl =
Z
γ1
F · ν dl +
On a
Z
1
F · ν dl =
1
F · ν dl = √
2
γ2
Z
1
Z
γ1
et
Z
1
F · ν dl = √
2
γ3
Z
Z
−1
0
0
1
Z
γ2
F · ν dl +
Z
γ3
F · ν dl .
(t, 0) · (0, −1)dt = 0;
√
(1 − t, t) · (1, 1) 2dt = 1
√
(−t, 1 − t) · (−1, 1) 2dt = 1.
11
5.2
Exercices
Exercice 5.2.1 Vérifier le théorème de la divergence dans les cas suivants :
1. A = triangle (0, 0), (1, 0), (0, 1), et F (x, y) = (x, y).
2. A = {(x, y) ∈ R2 : x2 + y 2 < 1} et F (x, y) = (y 2 , x).
3. A = {(x, y) ∈ R2 : 1 < x2 + y 2 < 4} et F (x, y) = (x2 y, 2xy).
4. A = {(x, y) ∈ R2 : x2 + (y − 1)2 < 1}, F (x, y) = (−x2 y, xy 2 ).
5. A = (x, y) ∈ R2 : x > 0 et x2 + y 2 < 1 , F (x, y) = (x, ϕ(y)) avec ϕ ∈ C 1 (R).
6. A = {(x, y) ∈ R2 : x2 + y 2 < 1} et F (x, y) = (xy, y 2 ).
12
Chapitre 6
Intégrales de surface
6.1
Définitions et propriétés
On donne des préliminaires sur les surfaces Σ ⊂ R3 .
Définition 6.1.1 On dit que Σ ⊂ R3 est une surface régulière s’il existe
1. A ⊂ R2 un ouvert borné dont le bord ∂A est une courbe simple fermée rǵulière par morceaux.
2. une paramétrisation σ : A → Σ, injective, de classe
normale

e1
σx ∧ σy = det  σx1
σy1
C 1 , σ(u, v) = (σ 1 (x, y), σ 2 (x, y), σ 3 (x, y)) telle que la

e2 e3
σx2 σx3  6= (0, 0, 0) .
σy2 σy3
On va donner la définition d’intégrale de surface d’un champ vectoriel.
Définition 6.1.2 Soit Σ ⊂ R3 une surface régulière (avec σ = (σ(x, y)), (x, y) ∈ A comme paramétrisation).
Soit F : Σ → R3 un champ continu. Alors on définit le flux de F à travers Σ comme
ZZ
ZZ
F · ds =
F (σ(x, y)) · (σx ∧ σy ) dx dy .
Σ
A
Exemple 6.1.3 Soient σ(x, y) = (x + y, 2y, x + y) avec (x, y) ∈ (0, 1) × (0, 1). Soit F (x, y, z) = (x + 1, y, z − 2).
Alors σx ∧ σy = (−2, 0, 2). Par conséquent
ZZ
ZZ
F · ds =
(x + y + 1, 2y, x + y − 2) · (−2, 0, 2) dx dy = −6 .
Σ
6.2
(0,1)×(0,1)
Exercices
P
Exercice 6.2.1 Soit
= (x, y, z) ∈ R3 : z = 6 − 3x − 2y; x, y, z ≥ 0 . Soit F (x, y, z) = (0, z, z). Calculer
le flux qui passe par cette surface.
Exercice 6.2.2 Soient F (x, y, z) = (y, −x, z 2 ) et Σ = {(x, y, z) ∈ R3 : z 2 = x2 + y 2 et 0 ≤ z ≤ 1}. Calculer le
flux passant à travers Σ.
13
Chapitre 7
Théorème de Stokes
7.1
Enoncé du théorème
Théorème 7.1.1 Soit Σ ⊂ R3 une surface régulière avec σ(x, y), (x, y) ∈ A une paramétrisation. Soit F :
Σ → R3 de classe C 1 (Σ; R3 ). Soit (x(t), y(t)), t ∈ [a, b] une paramétrisation de ∂A telle que ∂A est orienté
positivement. Alors
ZZ
Z
rot F · ds =
Σ
F · dl.
∂Σ
Remarque 7.1.2 Le théorème de Stokes nous dit que pour calculer la circuitation d’un
RR champ F le long d’une
courbe γ il suffit de choisir n’importe quelle surface Σ dont le bord est γ et calculer
rot F · ds .
Σ
Exemple 7.1.3 Soit γ(t) = (cos t, sin t, 3) avec t ∈ [0, 2π]. Soit F (x, y, z) = (x + y, z, z + 1). Si on veut calculer
la circuitation de F le long de γ il suffit
Z θ, r sin θ, 3) avec r ∈ [0, 1] et θ ∈ [0, 2π], et
Z Z de choisir σ(r, θ) = (rZcos
rot F · ds = −π .
rot F · ds. On trouve
calculer, grâce au théorème de Stokes
Σ
Σ
7.2
Exercices
Exercice 7.2.1 Vérifier le théorème de Stokes dans les cas suivants :
1. Σ = (x, y, z) ∈ R3 : x2 + y 2 = z 2 ; 0 < z < 1 et F (x, y, z) = (z, x, y).
2. Σ = (x, y, z) ∈ R3 : x2 + y 2 = z 2 ; 0 < z < 1 et F (x, y, z) = (x2 y, z 2 , 0).
3. Σ = (x, y, z) ∈ R3 : x2 + y 2 = z 4 ; 0 < z < 1 et F (x, y, z) = (x2 y, z, x).
4. Σ = (x, y, z) ∈ R3 : x2 + y 2 + z 2 = R2 ; z > 0 et F (x, y, z) = (x2 y 3 , 1, z).
P
5.
= le triangle de sommets A = (1, 0, 0), B = (2, 2, 0), C = (1, 1, 0) et F (x, y, z) = (0, x2 , 0).
√ P 6.
= (x, y, z) ∈ R3 : x2 + y 2 + z 2 = 4; x, y ≥ 0; 1 ≤ z ≤ 3 et F (x, y, z) = (0, z 2 , 0).
14
Chapitre 8
Appendice 1 : exemples de courbes et
surfaces
8.0.1
Exemples de courbes
1. Soit f : [a, b] → R une fonction. Son graphe est une courbe, dont une paramétrisation est
(t, f (t)) , t ∈ [a, b] .
2. Un cercle est une courbe, dont une paramétrisation est
(cos t, sin t), t ∈ [0, 2π] .
3. (t − sin t, 1 − cos t) pour t ∈ [0, 3] (cycloïde).
8.0.2
Exemples de surfaces
1. Soit f : A ⊂ R2 → R une fonction. Son graphe est une surface, dont une paramétrisation est
(x, y, f (x, y)) , (x, y) ∈ A .
2. (x2 + y 3 , 3y, sin(x y)) , (x, y) ∈ [0, 1] × [0, 1] est une surface.
3. Une sphère de centre (0, 0, 0) et de rayon r est une surface, dont une paramétrisation est
h π πi
r(cos θ cos ϕ, cos θ sin ϕ, sin θ) , (θ, ϕ) ∈ − ,
× [0, 2π] .
2 2
Remarque 8.0.2 Pourquoi cela est une paramétrisation d’une sphère ? Soit P = (x, y, z) un point sur
la sphère de rayon 1 et centre (0, 0, 0) (voir dessin). On rappelle que les points de la sphère satisfont
2
2
x
y2 +
z = 1. Soit H la projection de P sur le plan z = 0 : alors le triangle P HO est rectangle. Soit θ ∈
+
π π
ˆ : on a que |P H| = sin θ et |OH| = cos θ. Or, H est un point qui se trouve sur le cercle
− 2 , 2 l’angle P OH
de centre (0, 0, 0), rayon cos θ, dans le plan z = 0. Par conséquent on peut déterminer H à l’aide d’un angle
ϕ ∈π [0,π 2π] : H = (cos θ cos ϕ, cos θ sin ϕ, 0). Alors P = (x, y, z) = (cos θ cos ϕ, cos θ sin ϕ, sin θ) , (θ, ϕ) ∈
− 2 , 2 × [0, 2π].
4. σ(θ, z) = (r0 cos θ, r0 sin θ, z) , (θ, z) ∈ [0, 2π] × [0, H] est la surface latérale d’un cylindre de rayon r0 ,
hauteur H, axe l’axe z.
Remarque 8.0.3 Pourquoi cela est une paramétrisation d’un cylindre ? Il suffit d’imaginer un cylindre
comme l’union de cercles de rayon r0 , centre (0, 0), à hauteur z ∈ [0, H]. L’angle θ sert à déterminer la
position d’un point sur l’un des cercles qui composent le cylindre.
5. σ(z, θ) = (z tan α0 cos θ, z tan α0 sin θ, z) , (z, θ) ∈ [0, H] × [0, 2π] est la surface latérale d’un cône dont
l’angle d’ouverture est α0 , la hauteur est H, l’axe est l’axe z et le sommet est le point (0, 0, 0).
Remarque 8.0.4 Pourquoi cela est une paramétrisation d’un cône ? Soit P = (x, y, z) un point sur la
surface latérale du cône. Alors P appartient à un cercle de centre Pc = (0, 0, z) qui se trouve sur un plan
parallèle au plan xy à auteur z. Combient vaut le rayon |P Pc | de ce cercle ? On observe que le triangle
OPc P est rectangle. Par conséquent |P Pc | = z tan α0 . Pour déterminer la position de P sur ce cercle de
centre Pc et rayon z tan α0 on utilise l’angle θ.
15
Remarque 8.0.5 Les points P = (x, y, z) d’un cône dont l’angle d’ouverture est α0 et la hauteur est H
satisfont x2 + y 2 = z 2 tan2 α0 .
6. Soit γ(t) = (x(t), y(t)) , t ∈ [a, b] une courbe dans R2 . Si l’on fait une rotation autour de l’axe y on obtient
une surface. Une paramétrisation de la surface latérale est
(x(t) cos θ, x(t) sin θ, y(t)) , (t, θ) ∈ [a, b] × [0, 2π] .
Remarque 8.0.6 La sphère, le cylindre et le cône s’obtiennent de la rotation d’un demi-cercle, la droite
(r0 , z), la droite (t, at) respectivement.
16
z
1
P(x,y,z)
plan z=0
sin θ
θ
O
cos θ
H
y
x
1
rayon du cercle=
plan z=0
cos θ
H
ϕ
O
17
Chapitre 9
Appendice 2 : exemple d’interrogation
écrite et exemple de DS
9.1
Exemple d’interrogation écrite
Les documents et les calculatrices sont interdits. Toutes vos réponses doivent être justifiées et bien présentées.
Durée : 1 heure 30
Exercice 9.1.1 (6 points)
1. Soit F (x, y) = (x + y, x3 − ey ). Calculer div F et rot F .
√
2. Soit F (x, y, z) = (x2 + y − z, x + y, ln x2 − z). Calculer div F et rot F .
Soient f (x, y) = x + 3y et γ(t) le bord du carré de sommets (1, 0), (−1, 0), (0, 1), (0, −1). Calculer
Z
f ds.
γ
Soit F (x, y) = x − y, y 2 − x . Calculer
9.2
Z
γ
F · dl, pour γ = (t2 , et ) : t ∈ [0, 1] .
Exemple de DS
Les documents et les calculatrices sont interdits. Toutes vos réponses doivent être justifiées et bien présentées.
Durée : 1 heure 30
Exercice 9.2.1 (8 points) Soit
F (x, y) =
−
y
x
, 2
2
2
x + y x + y2
.
1) Trouver le domaine de définition de F .
2) Soit Ω = {(x, y) ∈ R2 : y > 0}. Montrer que F dérive d’un potentiel sur Ω. Après, trouver un tel potentiel.
Exercice 9.2.2 (12 points) Vérifier le théorème de Stokes pour
F (x, y, z) = (x2 y, z 2 , 0)
et
Σ = {(x, y, z) ∈ R3 : x2 + y 2 = z 2 , 0 ≤ z ≤ 1} .
18
Chapitre 10
Corrigés
19
10.1
Corrigé des exercices du chapitre Intégrales curvilignes
Corrigé de l’exercice 3.2.1 Soit f (x, y) = x2 + y 2 . Calculer
γ = segment entre (0, 0) et (M, 0) ;
On a γ(t) = (t, 0), avec t ∈ [0, M ]. Par conséquent
Z
Z
f ds =
Γ
M
0
γ
R
t2 ·
f ds dans les cas suivants :
√
1dt
γ = segment entre (0, 0) et (α, β)
β
t) avec t ∈ [0, α]. Par conséquent
On a γ(t) = (t, α
Z
α
Z
f ds =
0
γ
β2 2 p
2
t + 2 t · 1 + β 2 /α2 dt
α
γ = bord du carré (0, 0), (1, 0), (1, 1), (0, 1)
γ = γ1 ∪ γ2 ∪ γ3 ∪ γ4 où
γ1 (t) = (t, 0), avec t ∈ [0, 1] ;
γ2 (t) = (1, t), avec t ∈ [0, 1] ;
γ3 (t) = (1 − t, 1), avec t ∈ [0, 1] ;
γ4 (t) = (0, 1 − t), avec t ∈ [0, 1].
Par conséquent il suffit de faire la somme des quatre intégrales suivantes :
√
R1
R
f ds = 0 t2 · 1dt
γ1
√
R1
R
f ds = 0 [1 + t2 ] · 1dt
γ2
√
R1
R
f ds = 0 [(1 − t)2 + 1] · 1dt
γ3
√
R1
R
f ds = 0 (1 − t)2 · 1dt
γ4
Corrigé de l’exercice 3.2.2 Calculer
R
Γ
f ds dans les cas suivants :
f (x, y) = x; γ(t) = (cos t, sin t), 0 ≤ t ≤ 2π ;
On a
Z
Z
f dl =
2π
cos t
0
Γ
p
(− sin t)2 + (cos t)2 dt
√
f (x, y) = y ; γ(t) = (t − sin t; 1 − cos t), 0 ≤ t ≤ 2π.
On a
Z
Z 2π
p
√
1 − cos t · (1 − cos t)2 + (sin t)2 dt
f dl =
0
Γ
Corrigé de l’exercice 3.2.3 Calculer
Z
γ
1. f (x, y) = x; γ(t) = (t, t2 ), 0 ≤ t ≤ a ;
On a
Z
Z
f dl =
a
0
γ
2. f (x, y) = y 2 ; γ(t) = (t, et ), 1 ≤ t ≤ 3 ;
on a
Z
Z
1
γ
3. f (x, y) =
on a
e2t ·
γ(t) = (cos t, sin t), 0 ≤ t ≤
Z
γ
f dl =
Z
0
p
3
f dl =
x
1+y 2 ;
t·
π/2
1 + 4t2 dt = ...onpose1 + 4t2 = s
p
1 + e2t dt = ...onpose1 + e2t = s
π
2
;
√
cos t
1dt = ...onpose sin t = s
2 ·
1 + sin t
20
4. f (x, y) =
on a
p
1 − y 2 ; γ(t) = (cos t; sin t), 0 ≤ t ≤ π.
Z
f dl =
π
Z
p
√
1 − sin2 t · 1dt = ...trigo!
0
γ
Corrigé de l’exercice 3.2.4 Soit f (x, y) = x+2y. Calculer
Z
f dl si γ est le bord du trapèze (0, 0), (2, 0), (1, 1), (0, 1).
γ
On a γ = γ1 ∪ γ2 ∪ γ3 ∪ γ4 ∪ ou
1. γ1 (t) = (t, 0), t ∈ [0, 2]
2. γ2 (t) = (3 − t, t − 1), t ∈ [1, 2]
3. γ3 (t) = (1 − t, 1), t ∈ [0, 1]
4. γ4 (t) = (0, 1 − t), t ∈ [0, 1]
Par consequent
Z
Z
f dl =
γ
R2 √
t 1
0
√
R2
R
2. γ2 f dl = 1 [3 − t + 2(t − 1)] 2
√
R1
R
3. γ3 f dl = 0 [1 − t + 2] 1
√
R1
R
4. γ4 f dl = 0 2(1 − t) 1
1.
R
γ1
f dl +
γ1
Z
f dl +
γ2
Z
f dl +
γ3
Z
f dl
γ4
f dl =
Corrigé de l’exercice 3.2.5 Soient F (x, y) = (x + y, −x) et Γ = (x, y) ∈ R2 : y 2 + 4x4 − 4x2 = 0, x ≥ 0 .
1) Montrer que α(t) = (sin t, sin 2t) avec t ∈ [0, π] est une paramétrisation de Γ.
Z
2) Calculer F · dl.
Γ
On a, puisque α′ (t) = (cos t, 2 cos(2t))
Z
Z π
8
(sin t + sin(2t), − sin t) · (cos t, 2 cos(2t))dt =
F · dl =
3
0
Γ
Corrigé de l’exercice 3.2.6 Soient :
Calculer
Z
F (x, y) = xy, y 2 − x
Γ1 = {(t, t) : t ∈ [0, 1]}
Γ2 = (t, et ) : t ∈ [0, 1]
n√
o
Γ3 =
t, t2 : t ∈ [1, 2] .
F · dl, pour i = 1, 2, 3.
Γi
Z
Z
F · dl =
0
Γ1
Z
F · dl =
Γ2
Z
Γ3
F · dl =
Z
0
Z
1
1
0
(t2 , t2 − t) · (1, 1)
1
(t et , e2t − t) · (1, et )
√
√
1
(t2 t, t4 − t) · ( √ , 2t)
2 t
21
Corrigé de l’exercice 3.2.7 Soit C le cercle de centre (0, 0) et rayon 1. Soit F (x, y) = (x2 , y + x). Soit
γn (t) = (cos(nt), sin(nt)), n ≥ 1. Vérifier que
Z
Z
F · dl = n
F · dl
γn
En effet,
Z
γn
F · dl =
Z
γ1
γ1
2π
Z
(cos2 (nt), sin(nt) + cos(nt)) · (−n sin(nt), n cos(nt))dt
0
F · dl =
Z
2π
0
(cos2 t, sin t + cos t) · (− sin t, cos t)dt
Il suffit maintenant d’expliciter le produit scalaire et après d’utiliser la périodicité des fonctions trigonométriques.
Corrigé de l’exercice 3.2.8 Soit T le triangle de sommets (0, 0), (2, 2), (−2, 2). Soit F (x, y) = (x2 + 3, y + x).
Calculer
Z
F · ds
∂T
On a ∂T = γ1 ∪ γ2 ∪ γ3 , où
γ1 = (t, t), t ∈ [0, 2]
γ2 = (2 − t, 2), t ∈ [0, 4]
γ3 = (−2 + t, −t + 2), t ∈ [0, 2]
Par conséquent
Z
γ1
Z
F · ds =
γ2
Z
γ3
Z
F · ds =
2
0
[t2 + 3, 2t] · (1, 1)dt
4
Z
[(2 − t)2 + 3, 4 − t] · (−1, 0)dt
0
2
Z
F · ds =
0
[(t − 2)2 + 3, 0] · (1, −1)dt
Il suffit maintenant d’additionner les trois intégrales.
Corrigé de l’exercice 3.2.9 Soit C le cercle de centre (0, 0, 3) et rayon 2 qui se trouve sur le plan z = 3. Soit
F (x, y, z) = (x + 3, y + x, z + x). Calculer
Z
F · ds
∂C
∂C = {(2 cos t, 2 sin t, 3), t ∈ [0, 2π]}. Par conséquent
Z
∂C
F · ds =
Z
0
2π
(2 cos t + 3, 2 cos t + 2 sin t, 3 + 2 sin t) · (−2 sin t, 2 cos t, 0)dt = ...
Corrigé de l’exercice 3.2.10 Soit T le triangle de sommets (0, 0, 1), (2, 2, 1), (−2, 2, 1). Soit F (x, y, z) =
(y + z, x, −3z + y). Calculer
Z
F · ds
∂T
On a ∂T = γ1 ∪ γ2 ∪ γ3 , où
γ1 = (t, t, 1), t ∈ [0, 2]
γ2 = (2 − t, 2, 1), t ∈ [0, 4]
γ3 = (−2 + t, −t + 2, 1), t ∈ [0, 2]
Par conséquent
Z
γ1
Z
γ2
F · ds =
F · ds =
Z
2
0
Z
0
[t + 1, t, −3 + t] · (1, 1, 0)dt
4
[3, 2 − t, −3 + 2] · (−1, 0, 0)dt
22
Z
γ3
F · ds =
Z
2
0
[−t + 2 + 1, −2 + t, −3 − t] · (1, −1, 0)dt
Il suffit maintenant d’additionner les trois intégrales.
√
Corrigé de l’exercice 3.2.11 Soit γ(t) = (t2 , t + 1, t − 2), t ∈ [0, 1]. Soit F (x, y, z) = (y + z − 1, 3x, −3z + y).
Calculer
Z
F · ds
γ
Z
γ
F · ds =
Z
0
1
√
√
√
( t + 1 + t − 2 − 1, 3t2 , −3(t − 2) + t + 1) · (2t, 1/2 t, 1)dt = ...
Corrigé de l’exercice 3.2.12 Soit C = {(x, y, z) ∈ R3 : x2 + y 2 ≤ 1, z = 2, x ≥ 0, y ≥ 0}. Soit F (x, y, z) =
(x + 3, y + x, z + x). Calculer
Z
∂C
F · ds
∂C = γ1 ∪ γ2 ∪ γ3 ou
1. γ1 (t) = (t, 0, 2) avec t ∈ [0, 1]
2. γ2 (t) = (cos t, sin t, 2) avec t ∈ [0, π/2]
3. γ3 (t) = (0, 1 − t, 2) avec t ∈ [0, 1]
Par conséquent
R1
R
1. ∂γ1 F · ds = 0 (t + 3, t, 2 + t) · (1, 0, 0)
R1
R
2. ∂γ2 F · ds = 0 (cos t + 3, cos t + sin t, 2 + cos t) · (− sin t, cos t, 0)
R1
R
3. ∂γ3 F · ds = 0 (3, 1 − t, 2) · (0, −1, 0)
Il suffit maintenant d’additionner ces trois integrales.
23
10.2
Corrigé des exercices du chapitre Champs qui dérivent d’un potentiel
Corrigé de l’exercice 4.2.1 Soit F (x, y) = (4x3 y 2 , 2x4 y +y). Montrer que F dérive d’un potentiel sur Ω = R2
et trouver un tel potentiel.
F dérive d’un potentiel f car son ensemble de définition est R2 qui est convexe, et le roteur de F est nul. Pour
trouver f on écrit
∂f
∂f
= 4x3 y 2
= 2x4 y + y
∂x
∂y
En intégrant à la main on trouve
y2
+c
f (x, y) = x4 y 2 +
2
y
x
Corrigé de l’exercice 4.2.2 Soit F (x, y) = − 2
. Trouver le domaine de définition de F .
,
x + y 2 x2 + y 2
Soient
1. Ω1 = {(x, y) ∈ R2 : y > 0}
2. Ω2 = {(x, y) ∈ R2 : y < 0}
3. Ω3 = R2 \ {(x, y) ∈ R2 : x ≤ 0 , y = 0}
4. Ω4 = R2 \ {(0, 0)}
R
F dérive-t-il d’un potentiel sur Ωi ? Si oui trouver tel potentiel, sinon trouver Γ ⊂ Ωi tel que f · dl 6= 0
Γ
Le domaine de définition de F est R2 \ {(0, 0)} = Ω4 . Le roteur de F est 0.
Ω1 est convexe. Par conséquent F dérive d’un potentiel sur Ω1 . Tel potentiel est, par simple intégration à la
main
x
f (x, y) = − arctan + α+
y
Ω2 : la même analyse que dans le cas précédent conduit à
f (x, y) = − arctan
x
+ α−
y
Ω3 n’est pas convexe, donc on ne peut pas dire à priori que F dérive d’un potentiel. Puisque le roteur est nul,
cherchons à la main un potentiel f . S’il existe tel potentiel on doit avoir que f = − arctan xy + α+ pour
y > 0 et − arctan xy + α− pour y < 0. Il reste à savoir si l’on peut trouver des constantes α − + et α−
telles que F est continue. Cela est possible : il suffit de faire les limites pour y → 0+ et pour y → 0−
Ω4 n’est pas convexe. Montrons que f ne dérive pas d’un potentiel : il suffit de choisir comme courbe Γ le
cercle de centre 0 et rayon 1.
N.B. : Comment on a eu l’intuition que F ne dérive pas d’un potentiel sur Ω4 ? Il suffit de faire les limites
pour y → 0+ et pour y → 0− quand x < 0 !
Corrigé de l’exercice 4.2.3 Soit F (x, y, z) = (2x sin z, zey , x2 cos z + ey ). Montrer que F dérive d’un potentiel
sur R3 et trouver un tel potentiel.
rot F = 0 et R3 est convexe. Donc F dérive d’un potentiel sur R3 . Par simple intégration on trouve f (x, y, z) =
x2 sin z + zey + c
z
, x2 + 2yz, y 2 + arctgx). Le champ F dérive-t-il
Corrigé de l’exercice 4.2.4 Soit F (x, y, z) = (2xy +
1 + x2
d’un potentiel sur R3 ? Si oui, trouver ce potentiel.
Le potentiel est f (x, y, z) = x2 y + z arctan x + y 2 z + c
Corrigé de l’exercice 4.2.5 Soient les champs
F (x, y) =
et
G(x, y) =
−x
−y
, 2
2
2
2
(x + y ) (x + y 2 )2
y3
−xy 2
,
(x2 + y 2 )2 (x2 + y 2 )2
et soit Ω = R2 \ {(0, 0)}. Dérivent-ils d’un potentiel sur Ω ? (Si oui trouver ce potentiel, si non justifier votre
réponse).
24
1. Le roteur de F est nul, mais Ω n’est pas convexe, donc on ne peut pas dire à priori que F dérive d’un
potentiel f . Toutefois, si on le cherche à la main, on trouve f = 2(x21+y2 ) + c
2. Le roteur de F est nul, mais Ω n’est pas convexe, donc on ne peut pas dire à priori que F dérive d’un
potentiel f . En effet si C est le cercle de centre (0, 0) et rayon 1, on a que
Z
G · dl 6= 0 .
C
Corrigé de l’exercice 4.2.6 Démontrer que les champs suivants dérivent d’un potentiel
y
x + 2y
,
1. F (x, y) =
(x + y)2 (x + y)2
!
x
y
2. F (x, y) = p
,p
x2 + y 2
x2 + y 2
3. F (x, y) = 3x2 y − 2y 2 , x3 − 4xy .
Dans les trois cas on a que le roteur est 0.
1. Le domaine de définition de F n’est pas convexe. Toutefois, cherchons un potentiel à la main. Pour que f
soit un potentiel pour F on doit avoir que
y
1
x
∂f
=
=
−
∂y
(x + y)2
x + y (x + y)2
d’où
f (x, y) = ln |x + y| +
x
+c
x+y
2. Le domaine de définition de F n’est pas convexe. Toutefois, cherchons un potentiel à la main : on trouve,
par simple intégration,
p
f (x, y) = x2 + y 2 + c
3. Le domaine de définition de F est convexe, et donc F dérive d’un potentiel. En intégrant à la main on
trouve
f (x, y) = x3 y − 2y 2 x + c
Corrigé de l’exercice 4.2.7 Soit l’équation différentielle :
f2 (t, u(t)) u′ (t) + f1 (t, u(t)) = 0,
t ∈ R.
(10.1)
i) Soit F (x, y) = (f1 (x, y), f2 (x, y)) un champ vectoriel qui dérive d’un potentiel f sur R2 . Montrer qu’une
solution u = u(t) de (1) sous forme implicite est donnée par :
f (t, u(t)) = constante, ∀t ∈ R.
d
Suggestion : Calculer
f (t, u(t)) .
dt
ii) En déduire une solution de :
u2 (t)u′ (t) + sin t = 0.
u(0) = 3.
i) facile !
ii) on doit avoir f2 (t, u(t)) = u2 (t) et f1 (t, u(t)) = sin(t). Par conséquent
f2 (x, y) = y 2
d’où f (x, y) = − cos x +
y3
3
f1 (x, y) = sin x
+ c. Il suffit d’imposer maintenant la condition initiale.
25
10.3
Corrigé des exercices du chapitre Théorème de la divergence
dans le plan
Corrigé de l’exercice 5.2.1
1. La divergence de F vaut 2. Par conséquent
ZZ
divF dx dy = 2 mes(A) = 1.
Calculons
Z
F · ν dl
∂A
∂A est composé par
(a) γ1 (t) = (t, 0) avec t ∈ [0, 1]
(b) γ2 (t) = (1 − t, t) avec t ∈ [0, 1]
(c) γ3 (t) = (0, −t) avec t ∈ [−1, 0]
La normale unitée extérieure est (0, −1), √12 (1, 1) et (−1, 0) respectivement. Par conséquent il suffit d’additionner
Z
Z 1
√
(t, 0) · (0, −1) 1dt = 0
F · ν dl =
0
γ1
1
F · ν dl = √
2
Z
γ2
Z
F · ν dl =
γ3
1
Z
0
0
Z
−1
√
(1 − t, t) · (1, 1) 2dt = 1
√
(0, −t) · (−1, 0) 1dt = 0
2. A est le cercle de centre (0, 0) et rayon 1. La divergence de F vaut 0. Par conséquent
ZZ
divF dx dy = 0.
Calculons
Z
F · ν dl
∂A
On a ∂A = (cos t, sin t) avec t ∈ [0, 2π]. La normale unitée extérieure est (cos t, sin t). Par conséquent
Z
F · ν dl =
∂A
Z
0
2π
p
(sin2 t, cos t) · (cos t, sin t) sin2 t + cos2 tdt = 0
3. A est la couronne circulaire de centre (0, 0), de rayons 1 et 2. La divergence de F vaut 2xy + 2x. Alors,
en utilisant les coordonnées polaires
ZZ
ZZ
divF dx dy =
ρ(2ρ2 cos θ sin θ + 2ρ cos θ)dρ dθ = 0.
A
B
si B = {(ρ, θ) : θ ∈ [0, 2π], ρ ∈ [1, 2]}. Calculons
Z
F · ν dl .
∂A
∂A est composé par deux cercles : C2 , de rayon 2 et C1 de rayon 1. Le premier doit être parcouru au sens
anti-horaire, le deuxième au sens horaire. Calculons
Z
F · ν dl,
C2
26
C2 (t) = (2 cos t, 2 sin t) avec t ∈ [0, 2π]. La normale unitée extérieure est (cos t, sin t). Par conséquent
Z 2π
Z
p
(4 cos2 t 2 sin t, 2 2 sin t 2 cos t) · (cos t, sin t) 4 sin2 t + 4 cos2 tdt = 0
F · ν dl =
0
C2
Par ailleurs, calculons
Z
F · ν dl
C1
C1 (t) = (cos t, − sin t) avec t ∈ [0, 2π]. La normale unitée extérieure est (− cos t, sin t). Par conséquent
Z 2π
Z
p
(− cos2 t sin t, −2 cos t sin t) · (− cos t, sin t) sin2 t + cos2 tdt = 0
F · ν dl =
0
C1
4. A est le cercle de centre (0, 1) et rayon 1. La divergence de F vaut 0. Par conséquent
ZZ
divF dx dy = 0.
A
Calculons
Z
F · ν dl .
∂A
On a ∂A = (cos t, sin t + 1) avec t ∈ [0, 2π]. La normale unitée extérieure est (cos t, sin t). Par conséquent
Z
Z 2π
p
(− cos2 t(sin t + 1), cos t(sin t + 1)2 ) · (cos t, sin t) sin2 t + cos2 tdt = 0
F · ν dl =
0
∂A
5. A est le demi-cercle de centre (0, 1) et rayon 1. La divergence de F vaut 1 + ϕ′ (y). Par conséquent
ZZ
ZZ
π
ϕ′ (y)dx dy.
divF dx dy = +
2
A
p
2
2
Or, A = {(x, y) ∈ R : −1 ≤ y ≤ 1, 0 ≤ x ≤ 1 − y } Par conséquent
Z 1
ZZ
p
π
ϕ′ (y) 1 − y 2 dy.
divF dx dy = +
2
−1
Calculons
Z
F · ν dl .
∂A
∂A = S ∪ C où S(t) = (0, −t) avec t ∈ [−1, 1] et C(t) = (cos t, sin t) avec t ∈ [−π/2, π/2]. La normale
unitée extérieure est (−1, 0) et (cos t, sin t) respectivement. Par conséquent
Z
Z 1
√
(0, ϕ(−t)) · (−1, 0) 1dt = 0
F · ν dl =
−1
S
Z
C
F ν dl =
Z
π/2
−π/2
p
(cos t, ϕ(sin t)) · (cos t, sin t) sin2 t + cos2 tdt
p
R1
En faisant le changement de variables sin t = x et après en intégrant par parties, on trouve π2 + −1 ϕ′ (y) 1 − y 2 dy.
6. A est le cercle de centre (0, 0) et rayon 1. La divergence de F vaut 3y. En utilisant les coordonnées polaires
((ρ, θ) ∈ [0, 1] × [0, 2π]), on a
ZZ
divF dx dy = 0.
A
D’autre coté on a ∂A = (cos t, sin t) avec t ∈ [0, 2π]. La normale unitée extérieure est (cos t, sin t). Par
conséquent
Z
Z 2π
p
(cos t sin t, sin3 t) · (cos t, sin t) sin2 t + cos2 tdt = 0
F · ν dl =
∂A
0
27
10.4
Corrigé des exercices du chapitre Intégrales de surface
Corrigé de l’exercice 6.2.1 Soient F (x, y, z) = (y, −x, z 2 ) et Σ = {(x, y, z) ∈ R3 : z 2 = x2 + y 2 et 0 ≤ z ≤ 1}.
Calculer le flux passant à travers Σ.
On pose σ(θ, z) = (z cos θ, z sin θ, z) avec (θ, z) ∈ A = [0, 2π] × [0, 1]. On obtient σθ ∧ σz = (z cos θ, z sin θ, −z).
Par conséquent
ZZ
Z
(z sin θ, −z cos θ, z 2 ) · (z cos θ, z sin θ, −z)dz dθ
F · ds =
Σ
A
P Corrigé de l’exercice 6.2.2 Soit
= (x, y, z) ∈ R3 : z 2 = x2 + y 2 ; 0 ≤ z ≤ 1 . Soit F (x, y, z) = (x2 , y 2 , z 2 ).
Calculer le flux qui passe par cette surface.
On pose σ(θ, r) = (r cos θ, r sin θ, r) avec (θ, r) ∈ A = [0, 2π] × [0, 1]. On obtient σθ ∧ σr = (r cos θ, r sin θ, −r).
Par conséquent
Z
ZZ
F · ds =
(r2 cos2 θ, r2 sin2 θ, r2 ) · (r cos θ, r sin θ, −r)dr dθ
Σ
A
28
10.5
Corrigé des exercices du chapitre Théorème de Stokes
Corrigé de l’exercice 7.2.1
1. Le roteur de F est (1, 1, 1). Une paramétrisation de Σ est σ(θ, z) = (z cos θ, z sin θ, z) avec (θ, z) ∈ A =
[0, 2π] × [0, 1]. On a que σθ ∧ σz = (z cos θ, z sin θ, −z). Par conséquent
ZZ
Z 2π Z 1
(1, 1, 1) · (z cos θ, z sin θ, −z)dz = −π
dθ
rotF · ds =
Σ
0
0
Si on parcours le bord de A de facon positive on a
(a) (t, 0) avec t ∈ [0, 2π]
(b) (2π, t) avec t ∈ [0, 1]
(c) (2π − t, 1) avec t ∈ [0, 2π]
(d) (0, 1 − t) avec t ∈ [0, 1]
Par conséquent σ(∂A) est
(a) (0, 0, 0)
(b) (t, 0, t) avec t ∈ [0, 1]
(c) (cos t, − sin t, 1) avec t ∈ [0, 2π]
(d) (1 − t, 0, 1 − t) avec t ∈ [0, 1]
R
et donc ∂Σ F · dl est la somme des intégrales suivantes :
(a) 0
R1
R1
(b) 0 (t, t, 0) · (1, 0, 1) dt = 0 t dt
R 2π
R 2π
R 2π
(c) 0 (1, cos t, − sin t) · (− sin t, − cos t, 0) = 0 [− sin t − cos2 t] = 0 [− cos2 t]
R1
(d) 0 (1 − t, 1 − t, 0) · (−1, 0, −1) dt
2. On a rot F = (−2z, 0, −x2 ) Une paramétrisation de Σ est σ(θ, z) = (z cos θ, z sin θ, z) avec (θ, z) ∈ A =
[0, 2π] × [0, 1]. On a que σθ ∧ σz = (z cos θ, z sin θ, −z). Par conséquent
ZZ
Z 2π Z 1
π
(−2z, 0, −z 2 cos2 θ) · (z cos θ, z sin θ, −z)dz =
dθ
rotF · ds =
4
0
0
Σ
(a) (t, 0) avec t ∈ [0, 2π]
(b) (2π, t) avec t ∈ [0, 1]
(c) (2π − t, 1) avec t ∈ [0, 2π]
(d) (0, 1 − t) avec t ∈ [0, 1]
(a) (0, 0, 0)
(b) (t, 0, t) avec t ∈ [0, 1]
(c) (cos t, − sin t, 1) avec t ∈ [0, 2π]
(d) (1 − t, 0, 1 − t) avec t ∈ [0, 1]
R
(a) 0
R1
(b) 0 (0, t2 , 0) · (1, 0, 1) dt = 0
R 2π
R 2π
R 2π
R 2π
(c) 0 (− sin t cos2 t, 1, 0)·(− sin t, − cos t, 0) = 0 [sin2 t cos2 t−cos t] = 0 [sin2 t cos2 t]dt = 0 14 [sin 2t]2 dt
R1
(d) 0 (0, (1 − t)2 , 0) · (−1, 0, −1) dt = 0
3. On a rot F = (−1, −1, −x2 ). Une paramétrisation de Σ est σ(r, θ) = (r2 cos θ, r2 sin θ, r) avec A = (r, θ) ∈
[0, 1] × [0, 2π]. On a que σr × σθ = (−r2 cos θ, −r2 sin θ, 2r3 ). Par conséquent
ZZ
Z 1 Z 2π
π
(−1, −1, −r4 cos2 θ) · (−r2 cos θ, −r2 sin θ, 2r3 )dθ = −
dr
rotF · ds =
4
0
0
Σ
29
(a) (r, 0) avec r ∈ [0, 1]
(b) (1, θ) avec θ ∈ [0, 2π]
(c) (1 − r, 2π) avec r ∈ [0, 1]
(d) (0, 2π − θ) avec θ ∈ [0, 2π]
(a) (r2 , 0, r) avec r ∈ [0, 1]
(b) (cos θ, sin θ, 1) avec θ ∈ [0, 2π]
(c) ((1 − r)2 , 0, 1 − r) avec r ∈ [0, 1]
(d) (0, 0, 0)
R
R1
R1
(a) 0 (0, r, r2 ) · (2r, 0, 1)dr = 0 r2
R 2π
(b) 0 (cos2 θ sin θ, 1, cos θ) · (− sin θ, cos θ, 0)
R1
R1
(c) 0 [(1 − r)2 0, 1 − r, (1 − r)2 ] · [−2(1 − r), 0, −1]dr = − 0 (1 − r)2
(d) 0
4. On a rot F = (0, 0, −3x2 y 2 ). Une paramétrisation de Σ est σ(θ, ϕ) = R(cos θ sin ϕ, sin θ sin ϕ, cos ϕ) avec
(θ, ϕ) ∈ A = [0, 2π] × [0, π/2]. On a que σθ ∧ σϕ = −R2 sin ϕ(cos θ sin ϕ, sin θ sin ϕ, cos ϕ). Par conséquent
ZZ
ZZ
rotF ·ds =
(0, 0, −3R2 cos2 θ sin2 ϕR2 sin2 θ sin2 ϕ)·(−R2 sin2 ϕ cos θ, −R2 sin2 ϕ sin θ, −R2 sin ϕ cos ϕ)
Σ
A
= 3R
6
ZZ
cos2 θ sin2 θ sin5 ϕ cos ϕ .
A
(a) (θ, 0) avec θ ∈ [0, 2π]
(b) (2π, ϕ) avec ϕ ∈ [0, π/2]
(c) (2π − θ, π/2) avec θ ∈ [0, 2π]
(d) (0, π/2 − ϕ) avec ϕ ∈ [0, π/2]
(a) R(0, 0, 1) avec θ ∈ [0, 2π]
(b) R(sin ϕ, 0, cos ϕ) avec ϕ ∈ [0, π/2]
(c) R(cos θ, − sin θ, 0) avec ∈ [0, 2π]
(d) R(sin(π/2 − ϕ), 0, cos(π/2 − ϕ)) = R(cos ϕ, 0, sin ϕ) avec ϕ ∈ [0, π/2]
R
R 2π
(a) R 0 () · (0, 0, 0)dθ = 0
R π/2
(b) R 0 (0, 1, R cos ϕ) · (cos ϕ, 0, − sin ϕ)
R 2π
(c) R 0 [−R5 cos2 θ sin3 θ, 1, 0] · [− sin θ, − cos θ, 0]
R π/2
(d) R 0 (0, 1, R sin ϕ) · (− sin ϕ, 0, cos ϕ)
5. On a rot F = (0, 0, 2x). Une paramétrisation de Σ est σ(x, y) = (x, y, 0) avec (x, y) ∈ A = {(x, y) ∈ R2 :
1 ≤ x ≤ 2, 2x − 2 ≤ y ≤ x}. On a que σx ∧ σy = (0, 0, 1). Par conséquent
ZZ
ZZ
4
rotF · ds =
(0, 0, 2x) · (0, 0, 1) =
3
Σ
A
(a) (x, 2x − 2) avec x ∈ [1, 2]
(b) (2 − x, 2 − x) avec x ∈ [0, 1]
(c) (1, 1 − y) avec y ∈ [0, 1]
(a) (x, 2x − 2, 0) avec ∈ [1, 2]
30
(b) (2 − x, 2 − x, 0) avec ∈ [0, 1]
(c) (1, 1 − y, 0) avec ∈ [0, 1]
R
R2
(a) 1 (0, x2 , 0) · (1, 2, 0)
R1
R1
(b) 0 (0, (2 − x)2 , 0) · (−1, −1, 0) = − 0 (2 − x)2
R1
R1
(c) 0 (0, (1)2 , 0) · (0, −1, 0) = − 0 1
6. On a rot F = (−2z, 0, 0). Une paramétrisation de Σ est σ(θ, ϕ) = 2(cos θ sin ϕ, sin θ sin ϕ, cos ϕ) avec
(θ, ϕ) ∈ A = [0, π/2]×[π/6, π/3]. On a que σθ ∧σϕ = −22 sin ϕ(cos θ sin ϕ, sin θ sin ϕ, cos ϕ). Par conséquent
ZZ
ZZ
√
2
(−4cosϕ, 0, 0) · (−4 sin ϕ)(cos θ sin ϕ, sin θ sin ϕ, cos ϕ) = 2 3 −
rotF · ds =
3
A
Σ
(a) (θ, π/6) avec θ ∈ [0, π/2]
(b) (π/2, ϕ) avec ϕ ∈ [π/6, π/3]
(c) (π/2 − θ, π/3) avec θ ∈ [0, π/2]
(d) (0, π/2 − ϕ) avec ϕ ∈ [π/6, π/3]
(a) 2(cos θ sin(π/6), sin θ sin(π/6), cos(π/6)) = (cos θ, sin θ,
√
3) avec θ ∈ [0, π/2]
(b) 2(cos(π/2) sin ϕ, sin(π/2) sin ϕ, cos ϕ) = (0, 2 sin ϕ, 2 cos ϕ) avec ϕ ∈ [π/6, π/3]
√
√
(c) 2(cos(π/2 − θ) sin(π/3), sin(π/2 − θ) sin(π/3), cos(π/3)) = (sin θ 3, cos θ 3, 1) avec θ ∈ [0, π/2]
(d) 2(cos ϕ, 0, sin ϕ) avec ϕ ∈ [π/6, π/3]
R
R π/2
(a) 0 (0, 3, 0) · (− sin θ, cos θ, 0)dθ = 0
R π/3
(b) π/6 (0, 4 cos2 ϕ, 0) · (0, 2 cos ϕ, −2 sin ϕ)
√
√
R π/2
(c) 0 [0, 1, 0] · [ 3 cos θ, − 3 sin θ, 0]
R π/3
(d) π/6 (0, 4 sin2 ϕ, 0) · 2(− sin ϕ, 0, cos ϕ)
31
Chapitre 11
Retrouver ce cours sur le web : EUREKA
Eureka est un site Internet, où (entre autres) les enseignants de Mathématiques au Département de Génie
Electrique et Informatique Industrielle de l’IUT du Havre ont mis les documents des cours de la première année
et de la deuxième année : résumés des cours avec exercices (et corrigés), interrogations écrites, DS.
Voici les cours de Mathématiques donnés en GEII que l’on peut trouver sur Eureka :
– GEII mathématiques semestre 1 (1ère année)
– GEII mathématiques semestre 2 (1ère année)
– GEII S2-Mathématiques Numériques (1ère année)
– GEII mathématiques semestre 3 (2ème année)
– GEII-MCM1-Analyse vectorielle (module complémentaire 2ème année)
– GEII-MCM3-Probabilités et statistiques inférentielles (module complémentaire 2ème année)
COMMENT ACCEDER A EUREKA
1) Aller sur https ://eureka.univ-lehavre.fr
2) Cliquer sur "aide à l’utilisation des ressources informatiques pour les étudiants".
3) Cliquer sur "Comment connaître votre compte ?"
Identifiant : xycccccc
x=>1er caractère du nom
y => 1er caractère du prénom
cccccc => 6 derniers chiffres du code étudiant
mot de passe initial : jjmmaaaa (date de naissance)
par exemple, si la date de naissance est 2 juin 1981, le mot de passe sera 02061981
4) Cliquer sur "Comment activer votre compte ?"
Aller sur l’annuaire https ://intra-annuaire.univ-lehavre.fr (intranet ou WiFi)
=> "gérer son compte"
=> entrer votre identifiant et votre mot de passe
Lire la charte d’utilisation du réseau, valider le formulaire.
Si on veut, on peut changer son mot de passe.
Quitter l’annuaire : => menu "Navigation" de l’annuaire => "Déconnexion"
5) Revenir sur https ://eureka.univ-lehavre.fr ; entrer l’Identifiant et le mot de passe.
6) Cliquer sur DUT. Cliquer sur un cours qu’on veut consulter (s’inscrire).
32

Module complémentaire I de Mathématiques Département de Génie

Transcription

Documents pareils

Lycée Chrestien de Troyes - 2016/2017 - PCSI

Indications - Exercice 10 - XMaths

Formulaire de primitives

le cos vous propose une vente tupperware les cheques sont a l

note nitro circus et keen v - Pagesperso

TI-collège Plus

Exercices d`Analyse Complexe - MaPC41

III - Construction de FRESNEL

bac blanc 2009 - Lycée Camille Corot

Le double pendule - E