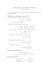Mouvements à Accélération Centrale

CHAPITRE 8
Mouvements à Accélération
Centrale
8.1 PROPRIÉTÉS GÉNÉRALES
8.1.1 Définition
Le mouvement du point M est un mouvement à accélération centrale dans le
repère (T), si et seulement si, il existe un point O de (T), tel que le vecteur
JJJJG
position OM du point M soit colinéaire au vecteur accélération du point M :
JJJJG
G( )
a T ( M , t ) = λ ( M ) OM ,
(8.1)
où λ(M) est un nombre réel dépendant ou indépendant du point M.
8.1.2 Un mouvement à accélération centrale est un
mouvement à trajectoire plane
Il résulte de la définition précédente qu'un mouvement est à accélération
centrale, si et seulement si :
JJJJG G ( )
G
OM ∧ a T ( M , t ) = 0 .
(8.2)
Or, nous avons la relation :
( ) JJJJG
JJJJG G (T )
G (T )
d T ⎡OM
⎤
∧
=
∧ a (M, t ) .
M
t
OM
(
,
)
v
⎦
dt ⎣
(8.3)
La comparaison de (8.2) et (8.3) montre donc qu'un mouvement est à accélération
centrale si et seulement si :
JJJJG G ( )
JG
OM ∧ v T ( M , t ) = C ,
(8.4)
JG
où C est un vecteur indépendant du temps.
8.1 Propriétés générales
101
JG
Si C est différent du vecteur nul, l'expression précédente montre que le point
M appartient
au plan passant par le point O et de direction orthogonale au
JG
vecteur C .
JG
Si C est le vecteur nul, la trajectoire est portée par une droite passant par le
point O.
8.1.3 Vitesse aréolaire
Le mouvement du point M étant un mouvement plan, il est possible de repérer
le point M par ses coordonnées polaires (r, α) dans ce plan (figure 8.1a).
Considérons alors (figure 8.1b) deux positions infiniment voisines M(t) et M(t +
dt) du point M sur sa trajectoire. Nous avons :
JJJJG
G
OM (t ) = r u (α ) ,
(8.5)
et
JJJJJJJJJJJJJJJG
G
( ) JJJJG
( )G
M (t ) M (t + d t ) = d T OM (t ) = d r u (α ) + r d T u (α )
(8.6)
G
G
= d r u (α ) + r u (α + π ) d α .
2
L'aire balayée par le segment OM est égale à l'aire de la surface dσ du triangle
OM(t)M(t + dt). Soit :
JJJJG
JJJJG
dσ = 1 OM (t ) ∧ dOM (t ) = 1 r 2dα .
(8.7)
2
2
La grandeur σ représente l'aire balayée entre une date prise comme origine des
temps et la date t. Sa dérivée par rapport au temps σ est appelée la vitesse
aréolaire du mouvement à la date t :
σ = dσ = 1 r 2α .
(8.8)
dt 2
La vitesse aréolaire représente l'aire balayée par unité de temps.
y
M(t + dt)
M(t)
G
u (α + π )
2
r
G
u (α )
α
M
x
O
O
(a)
(b)
FIGURE 8.1. Coordonnées polaires et aire balayée.
102
Chapitre 8 Mouvements à accélération centrale
8.1.4 Loi des aires
Dans le cas d'un mouvement plan, le vecteur vitesse du M point s'écrit d'après
(6.35) :
G( )
G
G
v T ( M , t ) = r u (α ) + rα u (α + π ) .
(8.9)
2
JG
Il en résulte que la relation (8.4) conduit à l'expression du vecteur C :
JG
G
G
C = r 2α k = C k ,
(8.10)
en posant :
C = r 2α .
(8.11)
JG
Le vecteur C étant indépendant du temps, il en résulte que C est également indépendant du temps. Par ailleurs en comparant à l'expression (8.8), nous obtenons :
σ = dσ = C .
dt
(8.12)
2
La constante C est alors appelée constante des aires.
Pour un mouvement plan à accélération centrale de centre O, la vitesse
aréolaire relative au point O est constante.
8.1.5 Expressions des vecteurs cinématiques
Les vecteurs cinématiques (6.29) et (6.33) peuvent être exprimés en
introduisant la constante des aires C exprimée en (8.11). Nous avons :
r = d r = d r dα = d r α = C2 d r = −C d 1 ,
d t dα d t dα
dα r
r dα
2
2
r = d r = d r α = C2 d ⎡−C d 1 ⎤ = − C2 d 2 1 ,
(8.13)
d t dα
r dα ⎣⎢ dα r ⎦⎥
r dα r
()
()
rα = C ,
r
D'où :
()
2
rα 2 = C2 .
r
()
G( )
G
G
v T ( M , t ) = −C u (α ) d 1 + C u (α + π ) ,
dα r
r
2
()
2 ⎡
2
G( )
⎤G
a T ( M , t ) = − C2 ⎢ 1 + d 2 1 ⎥ u (α ) .
r ⎣ r dα r ⎦
(8.14)
(8.15)
8.1.6 Équation polaire de la trajectoire
Dans le cas d'un mouvement à accélération centrale, l'expression (8.1) du
vecteur accélération s'écrit :
8.1 Propriétés générales
103
JJJJG
G( )
a T ( M , t ) = λ (r, α ) OM ,
(8.16)
où λ est un nombre réel qui dépend à priori de r et de α. Les équations de la dynamique (partie V) permettront de trouver l'expression de λ.
En introduisant dans la relation (8.16), les expressions (8.5) du vecteur position
et (8.15) du vecteur accélération, nous obtenons l'équation différentielle qui lie les
variables r et α :
()
d2 1 + λ r3 + 1 = 0 .
r
dα 2 r C 2
(8.17)
Cette équation permet de trouver r en fonction de α soit :
r = f (α ) ,
(8.18)
lorsque λ est connu. La loi des temps du mouvement sur la trajectoire est ensuite
obtenue à partir de (8.11) sous la forme :
2
d t = 1 r 2dα = 1 [ f (α )] dα .
C
C
(8.19)
Si α0 est la valeur de α à la date t, l'expression de t s'écrit :
t − t0 = 1
C
∫
α
α0
[ f (α )]2 dα .
(8.20)
8.1.7 Mouvements à accélération centrale pour lesquels
JJJJG
G(T )
2
a ( M , t ) = −ω OM
Le cas des mouvements rectilignes a été étudié au paragraphe 7.1.4, et nous
n'étudions donc dans ce paragraphe que le cas des mouvements curvilignes. Soit
(x, y, 0) les coordonnées cartésiennes du point M dans le plan (Oxy). Les coordonnées (x, y) vérifient les relations :
x = −ω 2 x
et
y = −ω 2 y .
(8.21)
D'où les équations du mouvement :
x = A cos ωt + B sin ωt ,
y = D cos ωt + E sin ωt ,
(8.22)
z = 0.
Nous choisissons une échelle des temps telle qu'à la date t = 0, le point M soit
en M0 tel que :
JJJJG
G
OM 0 = x0 i ,
(8.23)
avec une vitesse :
G
G
G
v0 = x0 i + y0 j .
(8.24)
104
Chapitre 8 Mouvements à accélération centrale
Les constantes A, B, D et E se calculent en fonction des conditions initiales x0 ,
x0 et y0 . Il en résulte que les équations de mouvement s'écrivent :
x = x0 cos ωt +
y=
y 0
ω
z = 0,
x0
ω
sin ωt ,
sin ωt ,
(8.25)
(en supposant ω > 0).
La trajectoire est alors une ellipse de centre O et d'équation :
( )
2
1 ⎛ x − x0 y ⎞ + ω y
⎜
y 0 ⎟⎠
y0
x0 2 ⎝
2
= 1.
(8.26)
La trajectoire est un cercle si x0 = 0 et y0 = ±ω x0 .
Quelle que soit la trajectoire, le mouvement est périodique, de période :
T = 2π .
(8.27)
C = x0 y 0 .
(8.28)
ω
La constante des aires est :
8.2 MOUVEMENTS À ACCÉLÉRATION CENTRALE
JJJJG
G (T )
OM
POUR LESQUELS a ( M , t ) = − K
OM 3
Nous étudions dans ce paragraphe les mouvements à accélération centrale pour
lesquels le vecteur accélération peut se mettre sous la forme :
JJJJG
G( )
(8.29)
a T ( M , t ) = − K OM3 ,
OM
où K est un nombre réel indépendant du point M.
8.2.1 Équations des trajectoires
L'équation des trajectoires s'obtient à partir de la relation (8.17) qui s'écrit ici :
()
d2 1 + 1 − K = 0
r C2
dα 2 r
(8.30)
Cette équation admet comme solution générale :
1 = K + A cos (α − α ) ,
0
r C2
(8.31)
JJJJG
G( )
8.2 Mouvements à accélération centrale pour lesquels a T ( M , t ) = − K OM3
OM
105
où A et α0 sont des constantes positives ou négatives déterminées par les conditions initiales (conditions à une date donnée). L'équation précédente peut être
réécrite sous la forme :
1 = K ⎡1 + AC 2 cos (α − α )⎤ .
(8.32)
0 ⎥
⎦
r C 2 ⎢⎣
K
Nous remarquons alors que la forme de cette équation ne change pas, lorsque
nous substituons au couple ( A, α 0 ) des constantes, le couple ( − A, α 0 + π ) . Sans
2
restreindre la généralité de l'étude, il est alors possible de choisir la quantité AC
K
positive. Nous posons :
2
e = AC ,
K
avec
e ≥ 0.
(8.33)
L'équation de la trajectoire s'écrit donc finalement :
1 = K [1 + e cos (α − α )] .
0
r C2
(8.34)
La trajectoire d'équation (8.34) s'obtient à partir de la courbe d'équation polaire
1 = K [1 + e cos α ] ,
r C2
(8.35)
en lui faisant subir une rotation de centre O et d'angle α0 .L'équation (8.35) représente en coordonnées polaires une conique d'excentricité e, de paramètre :
2
p=C ,
K
(8.36)
JJJG
dont l'un des foyers est le point O et d'axe focal Ox . L'équation (8.34) représente
JJG
donc une conique de foyer O, dont l'axe focal fait un angle α0 avec l'axe Ox .
Toutefois la condition r > 0 impose des restrictions suivant le signe de K.
8.2.2 Étude des trajectoires
8.2.2.1 Cas où K > 0
Le paramètre de la conique s'écrit :
2
p=C ,
K
(8.37)
et l'équation (8.34) de la trajectoire devient :
r=
p
1 + e cos ( α − α 0 )
.
(8.38)
106
Chapitre 8 Mouvements à accélération centrale
asymptote
y
y
p
p
axe
focal
O
X
P
axe
focal
α0
X
P
O
α0
x
x
(a) e > 1
(b) e = 1
Y
y
p
A
axe focal
C
O
X
P
α0
x
(c) 0 < e < 1
FIGURE 8.2. Trajectoires dans le cas où K > 0.
1. Si e > 1 , la trajectoire est la branche d'hyperbole qui tourne sa concavité vers
O (figure 8.2a). Le point P de plus petit rayon vecteur est appelé le péricentre :
p
OP = rp =
.
(8.39)
1+ e
2. Si e = 1 , la trajectoire est une parabole (figure 8.2b). Le péricentre est alors
défini par :
p
OP = rp = .
(8.40)
2
3. Si 0 < e < 1 , la trajectoire est une ellipse (figure 8.2c). Le péricentre est
donné par :
p
OP = rp =
.
(8.41)
1+ e
Le point A le plus éloigné de O est appelé l'apocentre :
OA = rA =
p
.
1− e
4. Si e = 0 , la trajectoire est un cercle de centre O.
(8.42)
JJJJG
G( )
8.2 Mouvements à accélération centrale pour lesquels a T ( M , t ) = − K OM3
OM
107
asymptote
y
axe focal
X
P
O
α0
x
FIGURE 8.3. Trajectoire dans le cas où K < 0.
8.2.2.2 Cas où K < 0
Lorsque K est négatif, le paramètre de la conique est :
2
p = −C ,
K
(8.43)
et l'équation (8.34) de la trajectoire se met sous la forme :
r=
−p
.
1 + e cos ( α − α 0 )
(8.44)
La condition que r soit positif impose que l'excentricité e soit supérieure à 1. La
trajectoire est la branche d'hyperbole (figure 8.3), qui tourne son côté convexe
vers O. Le péricentre est défini par :
OP = rp =
p
.
e −1
(8.45)
8.2.3 Intensité de la vitesse en un point de la trajectoire
G
G( )
Nous notons v le vecteur vitesse v T ( M , t ) en un point de la trajectoire.
D'après l'expression (8.14), nous avons :
()
2
2
G
v 2 = C 2 ⎡ d 1 ⎤ + C2 .
⎢⎣ dα r ⎥⎦
r
(8.46)
Soit en introduisant l'expression (8.34) de 1 :
r
2
G
v 2 = 2 K + K 2 (e2 − 1) ,
r C
(8.47)
108
Chapitre 8 Mouvements à accélération centrale
ou
(
)
G
v2 = 2 K + E ,
r
(8.48)
en posant :
2
(8.49)
E = 1 K 2 (e 2 − 1) .
2C
G2
Nous trouvons donc que la quantité v − K reste constante au cours du mouver
2
ment, soit :
G
v2 − K = E .
(8.50)
r
2
Le signe de E ne dépend (8.49) que de l'excentricité de la conique :
— si la trajectoire est elliptique, E < 0 ;
— si la trajectoire est une parabole, E = 0 ;
— si la trajectoire est une hyperbole, E > 0 .
8.2.4 Mouvement elliptique. Lois de Kepler.
8.2.4.1 Caractéristiques de la trajectoire elliptique
Dans le cas d'une trajectoire elliptique, l'équation de la trajectoire est donnée
par la relation (8.38), avec 0 ≤ e ≤ 1 . La distance entre le péricentre et l'apocentre
est égale au grand axe 2a de l'ellipse. Soit, d'après (8.41) et (8.42) :
a=
p
.
1 − e2
(8.51)
La distance c entre le centre C de l'ellipse (figure 8.2c) et le foyer O, appelée
distance focale est :
pe
,
(8.52)
c = a − OP =
1 − e2
d'où l'expression de l'excentricité :
e= c.
a
(8.53)
Dans le système d'axes (CXY) de l'ellipse (figure 8.2c), l'équation (8.35) de
l'ellipse s'écrit :
1
p = eX + ( X 2 + Y 2 ) 2 ,
(8.54)
( X + ae)2 Y 2
+ 2 = 1,
a2
b
(8.55)
ou en développant :
JJJJG
G( )
8.2 Mouvements à accélération centrale pour lesquels a T ( M , t ) = − K OM3
OM
109
avec
b 2 = a 2 (1 − e 2 ) .
(8.56)
Le paramètre b représente le demi-petit axe de l'ellipse.
Enfin, l'expression (8.49) montre que la constante E s'exprime dans le cas d'une
trajectoire elliptique sous la forme :
E=− K .
2a
(8.57)
Il en résulte que l'intensité de la vitesse (8.48) s'écrit :
(
)
G
v2 = K 2 − 1 .
r a
(8.58)
La vitesse est donc maximale au péricentre (point le plus proche du foyer) et
minimale à l'apocentre (point le plus éloigné).
8.2.4.2 Période de révolution
La vitesse aréolaire étant constante, le mouvement du point M sur la trajectoire
elliptique est périodique de période T, égale à la durée mise pour parcourir une
fois la trajectoire. Soit, d'après l'expression (8.12) :
π ab = 1 C T .
2
(8.59)
En tenant compte des relations (8.37), (8.51) et (8.56), la période de révolution
s'écrit :
T = 2π a3/2 .
K
(8.60)
8.2.4.3 Lois de Kepler
Les lois de Kepler regroupent certains des résultats établis dans ce chapitre et
peuvent être énoncées de la manière qui suit .
Si dans un repère, un point M a une accélération centrale de centre O fixe dans
ce repère et si la trajectoire de M n'a pas de branches infinies, il en résulte que :
1. La trajectoire du point M est une ellipse dont un des foyers est le point O.
2. La vitesse aréolaire de M relativement au point O est constante.
3. Le carré du temps de révolution est proportionnel au cube du grand axe de
l'ellipse.
Ces lois ont été établies sous des formes équivalentes par Kepler, à partir des
observations faites sur le mouvement des planètes.
110
Chapitre 8 Mouvements à accélération centrale
COMMENTAIRES
Une application particulièrement importante des mouvements à accélération centrale est celle des mouvements des planètes et de la Terre. Ces
mouvements dont les trajectoires sont des ellipses sont régies par les lois de
Kepler introduites dans ce chapitre. Le lecteur s'intéressera donc plus
particulièrement aux résultats établis au paragraphe 8.2.4. Ces résultats
seront utilisés au chapitre 19.