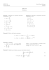1 Un développement asymptotique 〈〈 copy/paste 〉〉

843 - 2008/2009
1
DM 7 - corrigé
Un développement asymptotique
hh
copy/paste
ii
1. f est dérivable sur R, de dérivée f 0 (x) = 2 + 4x + 3x2 , trinôme de discriminant ∆ = 16 − 24 < 0,
donc f 0 est de signe constant > 0, donc f est continue, strictement croissante, avec f (x) −→+ −∞
x→0
et f (x) −→ +∞, donc réalise une bijection entre R∗+ et R. Dans la suite, on note g = f −1 sa
x→+∞
réciproque.
Fig. 1 – Graphes de f et de g
2. Attention, f réalise une bijection de R+ sur [1, +∞[ ; l’énoncé est donc faux. On sait cependant que
pour tout n ∈ N∗ ⊂ [1, +∞[, il existe un unique réel positif xn ∈ R+ , tel que f (xn ) = n (l’unique
antécédent de n par la bijection f , soit encore : xn = g(n)).
3. J’ai calculé un peu plus de termes que demandé :
seq(g(10**k),k=1..6);
1.365018995, 3.922991396, 9.310244955, 20.86717932, 45.74439392, 99.33110247
g(106 ) semble proche de 102 ...
4. f est croissante, donc sa bijection réciproque f −1 aussi. Et puisque xn = f −1 (n)...
Point de vue plus élémentaire : fixons n ∈ N et supposons xn+1 ≤ xn ; on a alors par croissance de
f , f (xn+1 ) ≤ f (xn ), c’est-à-dire n + 1 ≤ n : c’est absurde, ce qui prouve bien : f (xn ) < f (xn+1 ).
Supposons que (xn ) converge, et notons l sa limite. Dans la relation f (xn ) = n, le membre de
droite tend vers +∞ lorsque n tend vers +∞, et le membre de gauche vers f (l) par continuité de
f : c’est en contradiction avec l’unicité de la limite.
Ainsi, (xn ) est croissante et ne converge pas, donc : xn −→ +∞.
n→∞
√
3
3
5. f (x) ∼+∞ x et xn −→ +∞, donc f (xn ) ∼ xn ; or f (xn ) = n, donc x3n ∼ n, puis : xn ∼ 3 n.
n→∞
√
6. Puisque xn = 3 n(1 + αn ), l’équation f (xn ) = n devient :
n(1 + αn )3 + 2n2/3 (1 + αn )2 + 2n1/3 (1 + αn ) + 1 = n.
On laisse d’un côté tous les termes faisant intervenir αn et on passe de l’autre tous les autres. On
obtient alors :
3nαn + o(nαn ) = −2n2/3 + o(n2/3 ),
donc 3nαn ∼ −2n2/3 , puis :
αn ∼ −
1
2
3n−1/3
·
7. On a maintenant : xn = n1/3 −
2
+ o(1), donc :
3
√
2
xn − 3 n −→ − ·
n→∞
3
8. Avec ce qui précède, l’équation f (xn ) = n devient :
3
2
2
2
2
2/3
1/3
1 − 1/3 (1 + εn ) + 2n
1 − 1/3 (1 + εn ) + 1 = n
n 1 − 1/3 (1 + εn ) + 2n
3n
3n
3n
On retranche le terme principal, à savoir n. Les deux plus gros termes du membre de gauche
(±2n2/3 ) s’éliminent sans surprise. Il reste alors :
4
−2n2/3 εn + o(n2/3 εn ) − n1/3 + o(n1/3 ) + 2n1/3 + o(n1/3 ) = 0,
3
2
1
donc 2n2/3 εn + o(n2/3 εn ) = n1/3 + o(n1/3 ), et ainsi : εn ∼ 1/3 , et finalement :
3
3n
2 2
xn = n1/3 − − n−1/3 + o(n−1/3 ).
3 9
Si on laisse maple continuer, on obtient :
xn = n1/3 −
2
7
2 2 −1/3
− n
− n−2/3 + o(n−2/3 ).
3 9
81
Polynômes
2
1
1
1
1
1
1
1. (a) z 0 + 0 = 2 ; z 1 + 1 = z + , et enfin z +
= z 2 + 2 + 2, de sorte que z 2 + 2 =
z
z
z
z
z
z
2
1
− 2. Les polynômes P0 = 2, P1 = X et P2 = X 2 − 2 conviennent donc. Par ailleurs :
z+
z
3
1
3
1
= z 3 + 3z + + 3 ,
z+
z
z
z
de sorte que P3 = X 3 − 3X convient également.
(b) Ben heu...
1
1
1
1
tn + n
t+
= tn+1 + n+1 + tn−1 + n−1 ·
t
t
t
t
Cette relation se réécrit avantageusement :
1
1
1
1
tn+1 + n+1 = tn + n
t+
− tn−1 + n−1
t
t
t
t
ce qui peut donner une idée pour la suite...
(c) On définit, pour chaque
n ∈ N, la proposition Pn : hh il existe Pn ∈ R[X] tel que pour tout
1
1
∗
n
z ∈ C , Pn z +
= z + n · ii
z
z
– P a été vérifiée jusqu’au rang 3.
– Suposons la propriété vérifiée aux rangs n − 1 et n, pour un certain n ≥ 3, et montrons
P(n + 1). D’après P(n − 1) et P(n), on sait qu’il existe deux polynômes Pn−1 et Pn tels
que... Mais on a alors
1
1
1
1
n+1
z
+ n+1 = z +
Pn z +
− Pn−1 z +
,
z
z
z
z
∗
de sorte
qu’il suffit de considérer Pn+1 = XPn − Pn−1 pour avoir pour tout z ∈ C ,
1
1
Pn+1 z +
= z n+1 + n+1 · Ce qui établit P(n + 1).
z
z
2
Le principe de récurrence nous assure que P(n) est bien vérifiée pour tout n ∈ N.
2. (a) ϕ est impaire ; on ne l’étudiera que sur R∗ . Ses limites en 0+ et +∞ sont claires. Même
chose pour ses variations. Clairement, la droite d’équation y = x est asymptote au graphe
de ϕ en ±∞. Le changement de variation s’opère en 1. L’étude de ϕ nous assure : ϕ(R∗ ) =
] − ∞, −2] ∪ [2, +∞[.
Fig. 2 – Graphe de ϕ
(b) Si Pn et Qn répondent au problème, alors (Pn − Qn ) ϕ(t) = 0 pour tout t ∈ R∗ . Or ϕ(t)
prend une infinité de valeurs lorsque t décrit R∗ , donc Pn − Qn possède une infinité de racines,
donc est nul, et ainsi Pn = Qn .
0
si |z| < 2
(c) Il suffit de prendre f3 : z ∈ C 7→
P3 (z)
sinon
1
En effet, lorsque t ∈ R∗ , on a |ϕ(t)| ≥ 2, donc f3 ϕ(t) = P3 ϕ(t) = t3 + 3 ·
t
(d) Fixons z0 ∈ C. Pour z ∈ C∗ , l’équation ψ(z) = z0 est équivalente à z 2 − zz0 + 1 = 0. On
sait bien qu’une telle équation possède une ou deux solutions complexes. Ainsi, z0 possède au
moins un antécédent par ψ. Cette dernière application est donc surjective.
1
1
1
(e) La condition g3 z +
= z 3 + 3 = P3 z +
impose à g3 et P3 de coïncider sur tout
z
z
z
1
complexe de la forme z + , donc sur C d’après la question précédente, et ainsi : g3 = P3 .
z
3. (a) On peut constater à l’aide des Pk trouvés en début de problème que P0 (2 cos θ) = 2, P1 (2 cos θ) =
2 cos(θ) et P2 (2 cos θ) = (2 cos θ)2 − 2 = 4 cos2 θ − 2 = 2 cos(2θ), ce qui donne une petite idée
du résultat... et en effet :
1
1
iθ
Pn (2 cos θ) = Pn e + iθ = eniθ + niθ = 2 cos(nθ).
e
e
1 π
(b) Lorsque cos(nθ) = 0, on a Pn (2 cos θ) = 0. Ceci a lieu pour θ =
+ kπ pour tout k ∈ Z.
n 2
1 π
Mais lorsque k ∈ [[0, n − 1]], les réels
+ kπ sont distincts deux à deux et sont situés
n 2
dans ]0, π[, donc ont leur cosinus
distinctsπpar
injectivité du cosinus sur [0, π]. Ainsi, lorsque
k décrit [[0, n − 1]], les xk = cos (2k + 1)
constituent n racines distinctes de Pn .
2n
(c) On montrerait par récurrence (à l’aide de la formule de récurrence vérifiée par les Pn ) que
Pn est unitaire de degré n. Mais un polynôme de degré n admet au plus n racines distinctes.
Comme dans la question précédente, on en a effectivement exhibé n, le compte est bon et il y
en a exactement n. On a donc d’après le cours :
Pn =
n−1
Y
k=0
π ·
X − cos (2k + 1)
2n
1
Pn (2x)
4. On a Tn (cos θ) = cos(nθ) = Pn (2 cos θ). Si on note ∆ = Tn
, on a alors ∆(cos θ) = 0 pour
2
2
tout θ ∈ R, ce qui prouve que le polynôme ∆ possède une infinité de racines, donc est nul. Ainsi :
Tn =
3
Pn (2X)
·
2