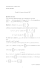Rang d`une matrice

Espace des lignes, espace des colonnes
Rang d’une matrice



Notation. Soit la matrice A : m×n A = 


A11

 A
A =  .21
 .
Am1


!lT
1
 
!
l2T
 

= .
  .
!lT
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
A=
!
A11| A12| . . . |A1n
"
!
"
!
a
!
a
.
.
.
|!
a
|
|
2
n
= # 1
$%
&
colonnes de A
m
a11 a12
a21 a22
..
..
am1 am2






 lignes de A





· · · a1n
· · · a2n
. . . ..
· · · amn





1
Définition. L’espace des lignes L(A) est le sous-espace de Rn
engendré par les lignes de la matrice A :
'
(
L(A) = !x ∈ Rn| ∃!z ∈ Rm : !xT = !z T A
c’est-à-dire les vecteurs de la forme
!x = AT !z = z1!l1 + z2!l2 + . . . + zm!lm
ou encore, dans une notation compacte :
)
'
(
L(A) = AT !z ) z ∈ Rm
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
2
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
3
Définition. L’espace des colonnes C(A) est le sous-espace de Rm
engendré par les colonnes de la matrice A :
Exemple.
C(A) = {!y ∈ Rm| ∃!x ∈ Rn : !y = A!x}
c’est-à-dire les vecteurs de la forme
!y = A!x = x1!a1 + x2!a2 + . . . + xn!an
C(A) = {A!x| !x ∈ Rn}
Remarque. On a ainsi L(A) = C(AT ) et C(A) = L(AT ).






$
$
les vecteurs de S avec S = 





L’espace des lignes L(A) est le sous-espace de R4 engendré par
4
2
2
1
5

0
0 

   

0 1
 ,   .
 1   1 


2
1 
 


,


2 2 1 5


A=0 0 1 2
0 1 1 1
3
L’espace des colonnes C(A) 
estle sous-espace
par
   de
 R engendré
 

2
1
5 
 2

       
les vecteurs de S avec S =  0  ,  0  ,  1  ,  2  .


 0
1
1
1 
ou encore, dans une notation compacte :
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL

 
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
5
Théorème. Les opérations élémentaires sur les lignes d’une matrice laissent inchangé son espace des lignes.
Pr. On montre que L(A) = L(EA) pour toute matrice élémentaire
E.
Soit !x ∈ L(A), c’est-à-dire qu’il existe !z ∈ Rm avec !xT = !z T A.
Soit w
! T = !z T E −1. Il vient !z T = w
! T E,
et ainsi !xT = !z T A = w
! T EA = w
! T (EA), donc !x ∈ L(EA).
!
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
6
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
7
Théorème. Les lignes non nulles de la matrice échelonnée réduite
R obtenue à partir de A forment une base de l’espace des lignes
L(A).
Pr. Par le théorème précédent, il suffit de montrer que les lignes
non nulles de R forment un ensemble linéairement indépendant. Or
chaque ligne i non nulle de R contient son 1-directeur qui est le seul
élément non nul dans sa colonne. Ainsi, la seule façon d’exprimer le
vecteur ligne nul comme combinaison linéaire des lignes non nulles
de R est de choisir des coefficients 0 pour chacune de ces lignes. !
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
Base de L(A) :
8
Exemple. Déterminer une base de l’espace des lignes de A avec


1 1 1 1


2 2 2 2
A=

1 2 2 2
2 3 3 3



On échelonne et réduit A et on obtient R = 

1
0
0
0
0
1
0
0
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
0
1
0
0
0
1
0
0





9
Théorème du rang






S= 





1
0
0
0
 


,

0

1

1
1











Théorème. Pour toute matrice A : m × n on a :
dim(L(A)) = dim(C(A))
On appelle rang de la matrice A ce nombre
rang(A) := dim(L(A)) = dim(C(A))
Pr.
Soit k la dimension de L(A) et B = {!v1, !v2, . . . , !vk }une base de
L(A).
Soit B : k × n la matrice ayant pour lignes les vecteurs de cette
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
10
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
11
base :
Il vient alors pour A


 !

"
!lT
B
g11 . . . g1k
"
 !1T 
 !

 l2 
 g21 . . . g2k B 



A=
 ..  = 

..


!
" 
!lT
gm1 . . . gmk B
m


g11 . . . g1k


 g21 . . . g2k 
 B = GB
= 


..


gm1 . . . gmk

!v1T
 !v T 


B =  .2 
 . 
!vkT
Chaque ligne de A s’écrit comme combinaison linéaire de B :

!lT = gi1!v T + . . . + gik!v T
1
k
i
c’est-à-dire
!lT =
i
!
"
gi1 . . . gik B
où G est une matrice m×k et B une matrice k×n. En décomposant
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
12
B en colonnes, il vient :
) 9 8
)
)
8 )
9 !
"
)
)!
)
) !
!
!
A = G b1) . . . )bn = Gb1) . . . )Gbn = !a1| . . . |!an
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
dim(C(A)) ≤ dim(L(A))
dim(L(A)) ≤ dim(C(A))
13
7
⇒ dim(L(A)) = dim(C(A))
On a ainsi montré que toute matrice A satisfait dim(C(A)) ≤
dim(L(A)). L’inégalité est donc aussi satisfaite par AT et on a
dim(C(AT )) ≤ dim(L(AT )). Mais, avec C(AT ) = L(A) et
L(AT ) = C(A) cette inégalité s’écrit dim(L(A)) ≤ dim(C(A)).
Finalement,
!
Par le théorème du rang, le rang d’une matrice est donc un nombre
bien défini et, pour déterminer ce nombre, il suffit de déterminer une
base de L(A).
Par convention, on pose pour toute matrice nulle Om×n,
rang(Om×n) = 0.
On obtient ainsi :
rang(A) = nombre de lignes non-nulles de la matrice échelonnée
réduite R.
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
Ainsi, chaque colonne de A est combinaison linéaire des colonnes de
G et donc
dim(C(A)) ≤ k = dim(L(A))
14
15
!
"T
Les deux premières lignes de A, à savoir 1 2 0 −3
et
!
"T
forment aussi une base de L(A). En effet, puis0 1 0 0
qu’on a obtenu R sans faire de permutations de lignes, les deux
premières lignes de R sont des combinaisons linéaires des deux
premières lignes de A.
Exemple.

Soit
1

A= 0
−1

1

R=0
0
On obtient
d’où

2 0 −3

1 0 0 
−2 0 3

0 0 −3

1 0 0 
0 0 0
On a donc dim(C(A)) = 2.
rang(A) = 2
Les deux premières lignes de R, à savoir
!
"T
forment une base de L(A).
0 1 0 0
!
1 0 0 −3
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL



A =

T
1
2
0
−3


0 −1


1 −2 

$
→R =
0 0 

0 3
"T
et
16
1
0
0
0

0 −1

1 0 

0 0 
0 0
Pour obtenir une base de C(A), on peut utiliser C(A) = L(AT )
et donc échelonner et réduire la matrice AT :
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
17
Théorème. Les colonnes de A correspondant aux colonnes directrices de R forment une base de C(A).
On constate
qu’on a bien dim(C(A))
= 2.
:!
"T !
"T ;
S=
est une base de C(A).
1 0 −1 , 0 1 0
!
"T !
"T
Comme précédemment, les vecteurs 1 0 −1 et 2 1 −2
forment également une base de C(A).
Pr. Soit r le nombre de lignes non nulles de R. On sait que
dim(C(A)) = r. Il suffit donc de montrer que les r colonnes de
A choisies sont bien linéairement indépendantes.
Soit A$ la sous-matrice de A ayant pour colonnes les r colonnes de
A choisies, et de manière analogue, R$ la sous-matrice de R ayant
pour colonnes les r colonnes directrices (ces colonnes sont donc les
r premières colonnes de la matrice identité Im).
Cependant, connaissant R, la matrice échelonnée réduite obtenue à
partir de A, le travail effectué précédemment pour déterminer une
base de C(A) est superflu.
A$ est équivalente par lignes à R$. En effet A est équivalente par
lignes à R, et en effectuant la même suite d’opérations élémentaires sur les lignes de A$ on aboutit alors à R$. Ainsi l’ensemble de
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
18
19
solutions du système A$!x = !0 est le même que celui du système
R$!x = !0. Or ce dernier système n’admet que la solution triviale,
puisque les colonnes de R$ sont des colonnes de la matrice identité.
Donc les colonnes de A$ sont bien linéairement indépendantes. !
Exemple.




A=


1 2 2
1 2 1
2 4 9
−1 −2 6
3 6 17
On en conclut








→R=




1
0
0
0
0
2
0
0
0
0
0
1
0
0
0







Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
20
Propriétés du rang d’une matrice
Théorème. Quelle que soit la matrice carrée A : n × n, les affirmations suivantes sont équivalentes :
1. A est inversible
2. rang(A) = n
3. dim(L(A)) = n
"T !
"T ;
et
2 0 , 0 0 1







2
1
9
6
17








 et






Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
21
Théorème. Soit les matrices A : m×n, B : m×n et D : n×p.
1. Si C : m × m est inversible, alors rang(CA) = rang(A)
2. rang(A) ≤ min(m, n)
3. rang(A + B) ≤ rang(A) + rang(B)
4. rang(AD) ≤ min(rang(A), rang(D))
Pr.
1. On a
4. dim(C(A)) = n
Pr. L’équivalence de 2. 3. et 4. n’est autre que le théorème du rang.
Pour montrer l’équivalence de 1. et 2. on se souvient qu’une matrice
A est inversible si et seulement si elle est équivalente par lignes à la
matrice identité I, c’est-à-dire L(A) = L(I), et L(I) = Rn. !
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
– rang(A) = 2
:!
– Une base de L(A) est
1
dim(L(A)) = 2



1






 1 


– Une base de C(A) est  2  ,





 −1 


 3
dim(C(A)) = 2
22
rang(A) = dim(L(A)) = dim(L(CA)) = rang(CA)
En effet, les premier et dernier signes égalité viennent de la définition du rang, celui du milieu du fait que C, étant inversible,
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
23
En effet, la première inégalité vient de ce que les lignes de A + B
sont évidemment des combinaisons
des lignes de A et des
< linéaires
=
A
lignes de B donc des lignes de
. La deuxième, de ce que le
B
nombre
= de lignes non nulles de la matrice échelonnée réduite de
<
A
est certainement inférieur ou égal a la somme de celui de
B
la matrice échelonnée réduite de A et de la matrice échelonnée
réduite de B (= rang(A) + rang(B)).
s’exprime comme produit de matrices élémentaires.
2. On a
dim(L(A)) ≤ m
dim(C(A)) ≤ n
et donc rang(A) = dim(L(A)) = dim(C(A)) ≤ min(m, n)
<
=
A
3. Considérant la matrice
on a
B
4. Chaque ligne de AD est combinaison linéaire des lignes de D.
Ainsi l’espace des lignes L(AD) est un sous-espace de L(D) et
<
=
A
rang(A + B) ≤ rang(
) ≤ rang(A) + rang(B)
B
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
rang(AD) = dim(L(AD)) ≤ dim(L(D)) = rang(D)
24
De même, chaque colonne de AD est combinaison linéaire des
colonnes de A. Ainsi
rang(AD) = dim(C(AD)) ≤ dim(C(A)) = rang(A)
!
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
26
Algèbre Linéaire - Th. M. Liebling, A. Prodon, ROSO-EPFL
25