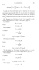Estimation de quantiles extrêmes pour les lois à queue de type

Transcription

Journal de la Société Française de Statistique
Vol. 154 No. 2 (2013)
Estimation de quantiles extrêmes pour les lois à
queue de type Weibull : une synthèse
bibliographique
Title: Extreme quantile estimation for Weibull-tail distributions: an overview
Laurent Gardes1 et Stéphane Girard2
Résumé : Cet article est une synthèse bibliographique des méthodes d’estimation de quantiles extrêmes pour les lois
à queue de type Weibull. Ces lois ont une fonction de survie qui décroit vers zéro à une vitesse exponentielle. Nous
montrons comment cette problématique s’inscrit plus largement dans la théorie des valeurs extrêmes.
Abstract: In this paper, an overview on extreme quantiles estimation for Weibull-tail distribution is provided. Recall
that the survival function of a Weibull-tail distribution decreases exponentially fast. We show how this problem can be
inserted in the more general setting of extreme value theory.
Mots-clés : Lois à queue de type Weibull, Synthèse bibliographique
Keywords: Weibull-tail distributions, Overview
Classification AMS 2000 : 62-00, 62G32
1. Introduction
Dans cet article, nous étudions le comportement des valeurs extrêmes d’un échantillon de variables
aléatoires unidimensionnelles. Nous nous concentrons essentiellement sur une famille particulière
de lois : les lois à queue de type Weibull. Ces lois ont une fonction de survie qui décroit vers zéro
à la vitesse exponentielle. Nous donnerons une définition plus précise de cette famille dans le
paragraphe 3. Notre principal objectif est de proposer des estimateurs de quantiles extrêmes. Plus
précisément, disposant d’un échantillon X1 , . . . , Xn de n variables aléatoires réelles indépendantes
et identiquement distribuées de fonction de répartition commune F(.), nous souhaitons estimer le
réel q(αn ) défini par
q(αn ) = F̄ ← (αn ), avec αn → 0 lorsque n → ∞,
où (αn ) est une suite connue et F̄ ← (u) = inf{x, F̄(x) ≤ u} est l’inverse généralisée de la fonction
de survie F̄(.) = 1 − F(.). Remarquons que q(αn ) est le quantile d’ordre 1 − αn de la fonction
de répartition F. Un problème similaire à l’estimation de q(αn ) est l’estimation de "petites
probabilités" pn . Autrement dit, pour une suite de réels (xn ) fixée, nous souhaitons estimer la
1
2
Université de Strasbourg & CNRS, IRMA, UMR 7501.
E-mail : [email protected]
INRIA Rhône-Alpes & LJK.
E-mail : [email protected]
Journal de la Société Française de Statistique, Vol. 154 No. 2 98-118
http://www.sfds.asso.fr/journal
© Société Française de Statistique et Société Mathématique de France (2013) ISSN: 2102-6238
Estimation de quantiles extrêmes pour les lois à queue de type Weibull : une synthèse bibliographique
99
probabilité pn définie par
pn = F̄(xn ), xn → ∞ lorsque n → ∞.
Ce sont les hydrologues qui ont été parmi les premiers à s’intéresser à ces deux problèmes.
Disposant d’un échantillon de hauteurs d’un cours d’eau, ils se sont posés les deux questions
suivantes :
1) quelle est la hauteur d’eau qui est atteinte ou dépassée pour une faible probabilité donnée ?
2) pour une "grande" hauteur d’eau fixée, qu’elle est la probabilité d’observer une hauteur
d’eau qui lui sera supérieure ?
Les questions 1) et 2) se rapportent donc respectivement à l’estimation d’un quantile extrême
(ou niveau de retour en hydrologie) et d’une "petite probabilité" (ou de façon équivalente en
hydrologie, période de retour). La difficulté principale réside dans le fait que l’on considère un
ordre de quantile αn → 0 (ou de manière équivalente un seuil xn → ∞). En effet, si par exemple
nαn → 0 lorsque n → ∞, il est clair que
P(Xn,n < q(αn )) = F n (q(αn )) = (1 − αn )n → 1
où X1,n ≤ . . . ≤ Xn,n est l’échantillon ordonné associé à X1 , . . . , Xn . La quantité q(αn ) n’appartient
donc pas à l’intervalle de variation de nos observations. En conséquence, l’estimateur de q(αn ) ne
peut être obtenu en inversant simplement la fonction de répartition empirique
F̂n (x) =
1 n
∑ I{Xi ≤ x},
n i=1
car F̂n (x) = 1 pour x ≥ Xn,n . L’estimation de quantiles extrêmes et/ou de "petites probabilités" est
requise dans de nombreux domaines d’application parmi lesquels citons la fiabilité (Ditlevsen
(1998)), la finance (Embrechts et al. (1997)), les assurances (Beirlant and Teugels (1992); Brodin
and Rootzén (2009)) et la climatologie (Rootzén and Tajvidi (2001)). Pour répondre à ces deux
questions, nous devons donc étudier de près le comportement de la queue de distribution de F(.)
en utilisant la théorie des valeurs extrêmes. Nous présentons les éléments essentiels de cette
théorie paragraphe 2. Dans le paragraphe 3, nous proposons des estimateurs de quantiles extrêmes
pour la famille des lois à queue de type Weibull.
2. Introduction à la théorie des valeurs extrêmes
Lorsque l’on s’intéresse à la partie centrale d’un échantillon, le résultat clé est le Théorème de
la Limite Centrale (abrégé en TLC) donnant la loi asymptotique de la somme des observations.
Par contre, si l’on souhaite étudier les valeurs extrêmes de cet échantillon, le TLC ne présente
que peu d’intérêt. On utilise plutôt un résultat établissant la loi asymptotique du maximum de
l’échantillon. Ce résultat est énoncé dans le paragraphe 2.1. Il permet de classer la plupart des lois
en trois domaines d’attraction. La caractérisation des fonctions de répartition dans chacun de ces
domaines est donnée dans le paragraphe 2.2.
100
L. Gardes & S. Girard
F IGURE 1. Exemples de densités associées à la loi des valeurs extrêmes (noir : γ = 0, bleu : γ = 1 et rouge : γ = −1).
2.1. Convergence en loi du maximum d’un échantillon
Le résultat ci-dessous établit la loi asymptotique du maximum Xn,n = max(X1 , . . . , Xn ) de l’échantillon. Il a été démontré notamment par Gnedenko (1943).
Théorème 1. S’il existe deux suites réelles (an > 0), (bn ) et un réel γ tels que
Xn,n − bn
P
≤ x → Hγ (x),
an
lorsque n → ∞ alors
(
Hγ (x) =
−1/γ
exp[−(1 + γx)+ ] si γ 6= 0,
exp(−e−x ) si γ = 0,
où y+ = max(0, y).
La fonction de répartition Hγ (.) est la fonction de répartition de la loi des valeurs extrêmes. La
densité associée est représentée Figure 1 pour différentes valeurs de γ. Cette loi dépend du seul
paramètre γ appelé l’indice des valeurs extrêmes. Selon le signe de γ, on définit trois domaines
d’attraction :
• si γ > 0, on dit que F(.) appartient au domaine d’attraction de Fréchet. Il contient les lois
dont la fonction de survie décroit comme une fonction puissance. On parle aussi de lois à
101
TABLE 1. Domaines d’attraction des lois usuelles.
Domaine
d’attraction
Loi
Gumbel
γ =0
Fréchet
γ >0
Weibull
γ <0
Normale
Exponentielle
Lognormale
Gamma
Weibull
Cauchy
Pareto
Student
Burr
Uniforme
Beta
queue lourde. Dans ce domaine d’attraction, on trouve les lois de Pareto, de Student, de
Cauchy, etc . . .
• si γ = 0, F(.) est dans le domaine d’attraction de Gumbel qui regroupe les lois ayant une
fonction de survie à décroissance exponentielle. C’est le cas des lois normale, gamma,
exponentielle, etc . . .
• si γ < 0, F(.) appartient au domaine d’attraction de Weibull. Ce domaine contient les lois
dont le point terminal xF = inf{x, F(x) ≥ 1} est fini. C’est le cas par exemple des lois
uniformes, lois beta, etc . . .
Un classement de nombreuses lois par domaine d’attraction est disponible dans (Embrechts et al.,
1997, Tableaux 3.4.2-3.4.4). Un extrait en est présenté Table 1. Nous allons à présent rappeler les
théorèmes de caractérisation des trois domaines d’attraction ci-dessus.
2.2. Caractérisation des domaines d’attraction
La caractérisation des domaines d’attraction fait largement appel à la notion de fonctions à
variations régulières. Rappelons qu’une fonction U(.) positive est à variations régulières d’indice
δ ∈ R à l’infini (on notera par la suite U(.) ∈ RV δ ) si pour tout λ > 0,
lim
x→∞
U(λ x)
= λδ.
U(x)
Si δ = 0, on dit que la fonction U(.) est à variations lentes (U(.) ∈ RV 0 ). On montre facilement
que toute fonction à variations régulières d’indice δ ∈ R s’écrit,
U(x) = xδ L(x), L ∈ RV 0 .
Rappelons enfin que toutes les fonctions à variations lentes L(.) s’écrivent sous la forme :
Z x
∆(u)
L(x) = c(x) exp
du ,
u
1
où c(x) → c > 0 et ∆(x) → 0 lorsque x → ∞. Cette représentation des fonctions à variations lentes
est connue sous le nom de représentation de Karamata (voir (Bingham et al., 1987, Théorème
1.3.1)). De plus, si la fonction c(.) est constante, la fonction L(.) est dite normalisée. De nombreux
résultats sur les fonctions à variations régulières sont donnés dans le livre de Bingham et al.
(1987).
102
2.2.1. Domaine d’attraction de Fréchet
Le résultat ci-dessous énoncé par Gnedenko (1943) et dont on trouvera une démonstration simple
dans le livre de (Resnick, 1987, Proposition 1.11) assure que toute fonction appartenant au
domaine d’attraction de Fréchet est une fonction à variations régulières.
Théorème 2. Une fonction de répartition F(.) appartient au domaine d’attraction de Fréchet
(avec un indice des valeurs extrêmes γ > 0) si et seulement si la fonction de survie F̄(.) ∈ RV −1/γ .
Autrement dit, une fonction de répartition F(.) appartenant au domaine d’attraction de Fréchet
s’écrit sous la forme :
F(x) = 1 − x−1/γ L(x), L(.) ∈ RV 0 .
(1)
Les suites de normalisation (an ) et (bn ) sont données dans ce cas par an = F̄ ← (1/n) et bn = 0
(voir (Resnick, 1987, Proposition 1.11)). Il faut aussi noter que toutes les fonctions de répartition
du domaine d’attraction de Fréchet ont un point terminal infini. On peut montrer (voir (Bingham
et al., 1987, Théorème 1.5.12)) que l’équation (1) est équivalente à :
q(α) = α −γ `(α −1 ), `(.) ∈ RV 0 ,
(2)
où α ∈ [0, 1]. De nombreux auteurs se sont intéressés à l’estimation de l’indice des valeurs
extrêmes γ et des quantiles extrêmes q(αn ) pour des lois à queue lourde. L’estimateur le plus
connu de γ > 0 est l’estimateur proposé par Hill (1975) et défini par
γ̂nH =
1 kn
∑ log(Xn−i+1,n ) − log(Xn−kn ,n ),
kn i=1
(3)
où (kn ) est une suite d’entiers telle que 1 < kn < n. D’autres estimateurs de cet indice ont
été proposés notamment par Beirlant et al. (2002, 1999) qui utilisent un modèle de régression
exponentiel pour débiaiser l’estimateur de Hill et par Feuerverger and Hall (1999) qui introduisent
un estimateur des moindres carrés. L’utilisation d’un noyau dans l’estimateur de Hill a été étudiée
par Csörgő et al. (1985). Un estimateur efficace de l’indice des valeurs extrêmes a été proposé
par Falk and Marohn (1997). Une liste plus détaillée des différents travaux sur l’estimation de
l’indice des valeurs extrêmes est effectuée par Csörgő and Viharos (1998). Concernant l’étude
du quantile extrême q(αn ), l’estimateur le plus fréquemment utilisé a été proposé par Weissman
(1978). Il est défini par :
H
kn γ̂n
W
q̂n (αn ) = Xn−kn +1,n
.
(4)
nαn
On peut trouver de nombreux autres estimateurs du quantile extrême dans le livre écrit par de Haan
and Ferreira (2006).
2.2.2. Domaine d’attraction de Weibull
Le résultat suivant (voir Gnedenko (1943), (Resnick, 1987, Proposition 1.13)) montre que l’on
passe du domaine d’attraction de Fréchet à celui de Weibull par un simple changement de variable
dans la fonction de répartition.
103
Théorème 3. Une fonction de répartition F(.) appartient au domaine d’attraction de Weibull
(avec un indice des valeurs extrêmes γ < 0) si et seulement si son point terminal xF est fini et si la
fonction de répartition F∗ (.) définie par
0
si x < 0
F∗ (x) =
F(xF − 1/x) si x ≥ 0,
appartient au domaine d’attraction de Fréchet avec un indice des valeurs extrêmes −γ > 0.
Ainsi, une fonction de répartition F(.) du domaine d’attraction de Weibull s’écrit pour x ≤ xF :
F(x) = 1 − (xF − x)−1/γ L((xF − x)−1 ), L(.) ∈ RV 0 .
(5)
De manière équivalente, le quantile q(α) associé s’écrit :
q(α) = xF − α −γ `(1/x), `(.) ∈ RV 0 .
(6)
Les suites de normalisation (an ) et (bn ) sont données par an = xF − F̄ ← (1/n) et bn = xF . Ce
domaine d’attraction a été considéré notamment par Falk (1995), Girard et al. (2012) et Hall and
Park (2002) pour estimer le point terminal d’une distribution.
2.2.3. Domaine d’attraction de Gumbel
La caractérisation des fonctions de répartition du domaine d’attraction de Gumbel est plus
complexe. Le résultat ci-dessous est démontré notamment dans (Resnick, 1987, Proposition 1.4).
Théorème 4. Une fonction de répartition F(.) appartient au domaine d’attraction de Gumbel si
et seulement si il existe z < xF ≤ ∞ tel que
Zx
1
F̄(x) = c(x) exp −
dt , z < x < xF ,
(7)
z a(t)
où c(x) → c > 0 lorsque x → xF et a(.) est une fonction positive et dérivable de dérivée a0 (.) telle
que a0 (x) → 0 lorsque x → xF .
Le domaine d’attraction de Gumbel regroupe une grande diversité de lois comptant parmi elles
la plupart des lois usuelles (loi normale, exponentielle, gamma, log-normale). Cette famille
étant difficile à étudier dans toute sa généralité, de nombreux auteurs se sont concentrés sur une
sous-famille : les lois à queue de type Weibull. Leur définition est donnée dans le paragraphe
suivant.
3. Inférence pour les lois à queue de type Weibull
Les lois à queue de type Weibull correspondent au cas particulier où l’on suppose dans (7) que
la dérivée de la fonction a(.) est à variations régulières avec un indice strictement négatif. Plus
précisément, si on suppose que a0 (.) ∈ RV −1/θ où θ > 0 est appelé l’indice de queue de Weibull,
on montre facilement que l’équation (7) s’écrit :
n
o
F̄(x) = exp −x1/θ L(x) , L(.) ∈ RV 0 .
(8)
104
Une fonction de répartition s’écrivant selon le modèle (8) est dite à queue de type Weibull d’indice
θ > 0. L’équation (8) est équivalente à
q(α) = (− log α)θ `(− log α), `(.) ∈ RV 0 ,
(9)
où α ∈ [0, 1]. Cette famille de lois contient par exemple les lois normale, Gamma, exponentielle,
etc . . . Par contre, la loi log-normale qui appartient au domaine d’attraction de Gumbel n’est pas
une loi à queue de type Weibull. Dans la suite, on considère un échantillon X1 , . . . , Xn de variables
aléatoires indépendantes et distribuées selon le modèle (8). Le paragraphe 3.1 est consacré à
l’estimation de l’indice de queue de Weibull. L’estimation des quantiles extrêmes est discutée
dans le paragraphe 3.2.
3.1. Estimation de l’indice de queue de Weibull
Les lois à queue de type Weibull appartiennent évidemment au domaine d’attraction de Gumbel
(i.e. avec un indice des valeurs extrêmes γ = 0). L’indice des valeurs extrêmes ne fournit donc
aucune information sur la vitesse de décroissance de la fonction de survie à l’intérieur de cette
famille de loi. C’est l’indice de queue de Weibull θ qui nous donne cette information : une valeur
de θ proche de zéro (resp. l’infini) correspond à une décroissance rapide (resp. lente) de la queue
de distribution. La connaissance de ce paramètre est donc essentielle si l’on souhaite par exemple
estimer un quantile extrême. Il existe dans la littérature de nombreux estimateurs de l’indice θ .
Berred (1991) propose un estimateur basé sur des valeurs records mais la majorité des estimateurs
utilise les kn plus grandes observations de l’échantillon. Parmi ceux-ci citons Beirlant et al. (2006,
1995, 1996), Broniatowski (1993), Diebolt et al. (2008a), Dierckx et al. (2009), Gardes and Girard
(2006, 2008), Girard (2004) Goegebeur et al. (2010); Goegebeur and Guillou (2010). Le plus
simple d’entre eux a été proposé dans Beirlant et al. (1996). Il est défini par :
,
θ̂nB =
kn −1
kn −1
∑ (log(Xn−i+1,n ) − log(Xn−k +1,n ))
n
i=1
∑ (log log(n/i) − log log(n/kn )) ,
(10)
i=1
et rappelons que (kn ) est une suite d’entiers tels que 1 < kn < n. Son expression est proche de
celle de l’estimateur de l’indice des valeurs extrêmes proposé par Hill (1975) (voir l’équation (3)).
Elle est basée sur la remarque suivante : d’après (9),
log q(α)
log `(log(1/α))
=θ+
.
log log(1/α)
log log(1/α)
Ainsi, comme log(`(x))/ log(x) → 0 lorsque x → ∞ (voir (Bingham et al., 1987, Propriété 1.3.6)),
on en déduit que pour α → 0,
log q(α) ∼ θ log log(1/α).
(11)
Ainsi, les points (log log(n/i), log(Xn−i+1,n )), i = 1, . . . , kn − 1 sont approximativement répartis
sur une droite de pente θ . Nous détaillons dans les paragraphes 3.1.1 et 3.1.2 deux familles d’estimateurs englobant θ̂nB ainsi qu’un estimateur débiaisé de l’indice θ (voir le paragraphe 3.1.3). Les
résultats asymptotiques sont obtenus (entre autres) sous les hypothèses suivantes.
105
TABLE 2. Paramètres θ , ρ et fonction b(.) associés aux lois usuelles. Les paramètres α et λ sont respectivement des
paramètres de forme et d’échelle.
Loi
θ
b(x)
ρ
Normale N (µ, σ 2 )
1/2
1 log x
4 x
−1
Gamma Γ(α 6= 1, λ )
1
Weibull W (α, λ )
1/α
(1 − α)
0
log x
x
−1
−∞
(H.1) La suite (kn ) vérifie kn → ∞ et n/kn → ∞ lorsque n → ∞.
(H.2) Il existe un paramètre ρ < 0 et une fonction b(.) vérifiant b(x) → 0 lorsque x → ∞ tels
que pour tout 1 < A < ∞
log(`(λ x)/`(x))
lim sup − 1 = 0,
x→∞ λ ∈[1,A]
b(x)Kρ (λ )
où Kρ (λ ) =
R λ ρ−1
dt et `(.) est la fonction à variations lentes introduite dans (9).
1 t
L’hypothèse (H.1) assure que le nombre de statistiques d’ordre conservées kn est assez grand
(kn → ∞) pour obtenir des estimateurs stables, mais pas trop (n/kn → ∞) pour que les observations
utilisées restent dans la queue de distribution. Le choix de la suite (kn ) est donc un compromis
entre le biais et la variance de l’estimateur.
L’hypothèse (H.2) est très souvent utilisée pour étudier le comportement asymptotique d’estimateurs d’indice ou de quantiles extrêmes. Elle est notamment nécessaire pour démontrer la normalité
asymptotique de l’estimateur de Hill défini en (3). On peut montrer (voir par exemple Geluk and
Haan (1987)) que la fonction b(.) (appelée aussi fonction de biais) est à variations régulières
d’indice ρ < 0. Le paramètre ρ (appelé paramètre du second ordre) contrôle donc la vitesse de
convergence de `(λ x)/`(x) vers 1. Une valeur de ρ proche de 0 implique une faible vitesse de
convergence. Quelques exemples en sont donnés dans la Table 2.
3.1.1. Utilisation de poids
Nous nous focalisons sur la famille d’estimateurs Gardes and Girard (2008) de θ incorporant des
poids dans l’estimateur θ̂nB défini par (10). Les estimateurs obtenus sont donc des combinaisons
linéaires de statistiques d’ordre c’est-à-dire des L-estimateurs. Plus précisément, on considère la
famille d’estimateurs Θ1 = {θ̂n (ζ ), ζ = (ζ1,n , . . . , ζkn −1,n )} avec
,
kn −1
θ̂n (ζ ) =
kn −1
∑ ζi,n (log(Xn−i+1,n ) − log(Xn−k +1,n ))
n
i=1
∑ ζi,n (log log(n/i) − log log(n/kn )) ,
i=1
(12)
106
où ζi,n = W (i/kn ) + εi,n , (εi,n ), i = 1, . . . , kn − 1 étant une suite non-aléatoire. La fonction déterministe W (.) doit satisfaire les deux hypothèses de régularité ci dessous :
(H.3) la fonction W (.) est définie et admet une dérivée continue sur l’intervalle ]0, 1[.
(H.4) Il existe M > 0, 0 ≤ q < 1/2 et p < 1 tels que pour tout x ∈]0, 1[, |W (x)| ≤ Mx−q et
|W 0 (x)| ≤ Mx−p−q .
Ces conditions sont essentielles pour établir la normalité asymptotique des L-estimateurs (voir
par exemple Mason (1981)). On pose :
kεkn,∞ = max |εi,n |, µ(W ) =
1,...,kn −1
2
Z 1Z 1
σ (W ) =
W (x)W (y)
0
0
Z 1
W (x) log(1/x)dx,
0
min(x, y) − xy
dxdy.
xy
Nous rappelons à présent (voir (Gardes and Girard, 2008, Théorème 1)) le résultat de normalité
asymptotique des estimateurs appartenant à cette famille.
Théorème 5. On se place sous le modèle (8) et on suppose que les conditions (H.1) à (H.4)
1/2
1/2
sont satisfaites. Si kn b(log(n/kn )) → Λ ∈ R et kn max{1/ log(n), kεkn,∞ } → 0 lorsque n → ∞
alors,
d
1/2
kn (θ̂n (ζ ) − θ − b(log(n/kn ))) → N (0, θ 2 σ 2 (W )/µ 2 (W )).
Dans le cas où lim inf kεkn,∞ log(n) ≤ 1 avec Λ 6= 0, le Théorème 5 n’est valable que si ρ > −1
ce qui correspond à une vitesse de convergence lente dans la condition (H.2). Donnons à présent
deux choix possibles pour les poids ζi,n , i = 1, . . . , kn − 1.
En prenant ζi,n = 1 pour tout i = 1, . . . , kn − 1 (i.e. W (x) = 1 pour tout x ∈]0, 1[ et εi,n =
0 pour tout i = 1, . . . , kn − 1), on retrouve l’estimateur θ̂nB proposé par Beirlant et al. (1996)
(voir l’équation (10)). Le résultat de normalité asymptotique établi par Girard (2004) est une
conséquence directe du Théorème 5. Nous rappelons ce résultat ci-dessous :
Corollaire 1. On se place sous le modèle (8) et on suppose que les conditions (H.1) et (H.2) sont
d
1/2
1/2
1/2
satisfaites. Si kn b(log(n/kn )) → 0 et kn / log(n) → 0 alors kn (θ̂nB − θ ) → N (0, θ 2 ).
En rappelant que les points (log log(n/i), log(Xn−i+1,n )), i = 1, . . . , kn − 1 sont approximativement répartis sur une droite de pente θ , il est possible d’estimer θ par l’estimateur des moindres
carrés. Il est montré dans (Gardes and Girard, 2008, Corollaire 2) que l’estimateur des moindres
carrés appartient à la famille Θ1 avec les poids :
Z
ζi,n = ζi,n
= log log(n/i) −
1 kn −1
∑ log log(n/i) = W (i/kn ) + εi,n ,
kn − 1 i=1
où W (x) = −(log(x) + 1) et, uniformément en i = 1, . . . , kn − 1, εi,n = O(log2 (kn )/ log(n)) +
O(log(kn )/kn ). L’estimateur θ̂n (ζ Z ) ainsi obtenu est similaire à l’estimateur de l’indice des
107
valeurs extrêmes de Zipf introduit par Kratz and Resnick (1996) et Schultze and Steinebach
(1996) dans le cas de lois à queue lourde. Nous rappelons ci-dessous le résultat sur la normalité
asymptotique de θ̂n (ζ Z ) (voir (Gardes and Girard, 2008, Corollaire 2)). C’est une conséquence
directe du Théorème 5.
Corollaire 2. On se place sous le modèle (8) et on suppose que les conditions (H.1) et (H.2)
d
1/2
1/2
1/2
sont satisfaites. Si kn b(log(n/kn )) → 0 et kn log2 (kn )/ log(n) → 0 alors kn (θ̂n (ζ Z ) − θ ) →
N (0, 2θ 2 ).
3.1.2. Utilisation d’autres suites de normalisation
Dans l’estimateur θ̂nB (voir l’équation (10)), la somme des écarts entre les logarithmes des
statistiques d’ordre est normalisée par la suite :
(1)
Tn
kn −1
=
∑ (log log(n/i) − log log(n/kn )).
(13)
i=1
(1)
Il est possible de remplacer cette suite (Tn ) par une suite positive quelconque (Tn ). Ceci conduit
à définir la famille d’estimateurs Θ2 = {θ̂n (Tn ), Tn > 0} avec
θ̂n (Tn ) =
1 kn −1
∑ (log(Xn−i+1,n ) − log(Xn−kn +1,n )).
Tn i=1
(14)
En posant
log(1 + x/t)e−x dx
− 1,
Tn
on obtient (Gardes and Girard, 2006, Théorème 2.1) un résultat de normalité asymptotique pour
cette famille d’estimateurs. Ce résultat est rappelé ci-dessous :
un =
kn
R∞
0
Théorème 6. On se place sous le modèle (8) et on suppose que les conditions (H.1) et (H.2) sont
1/2
satisfaites. Si Tn kn log(n/kn ) → 1 et kn b(log(n/kn )) → Λ ∈ R lorsque n → ∞ alors
1/2
d
kn (θ̂n (Tn ) − θ − b(log(n/kn )) − θ un ) → N (0, θ 2 ).
La meilleure vitesse de convergence de θ̂n (Tn ) est obtenue lorsque Λ 6= 0. Dans ce cas, on
peut montrer (voir (Gardes and Girard, 2006, Proposition 2.2)) que (kn ) est équivalente à
Λ2 (log n)−2ρ `∗ (log(n)) où `∗ (.) est une fonction à variations lentes. Sous l’hypothèse supplémentaire lim inf kεkn,∞ log(n) ≤ 1, les estimateurs de la famille Θ1 ont la même vitesse de convergence
que ceux de la famille Θ2 . Le Théorème 6 permet de déterminer l’erreur moyenne quadratique
asymptotique (AMSE) de θ̂n (Tn ). Elle est donnée par
AMSE(θ̂n (Tn )) = (θ un + b(log(n/kn )))2 +
θ2
.
kn
(15)
Le terme de variance asymptotique est donc identique pour tous les estimateurs de la famille. Le
biais dépend par contre du choix de la suite (Tn ). Le choix idéal pour cette suite de normalisation
108
serait donc de prendre Tn de telle sorte que θ un + b(log(n/kn )) = 0. Malheureusement, θ et
la fonction de biais b(.) sont inconnus et il est donc impossible de définir une telle suite (Tn ).
Donnons à présent quelques choix possibles pour cette suite.
(1)
Comme nous l’avons déjà mentionné, le choix (Tn ) = (Tn ) (voir l’équation (13)) conduit
(1)
à l’estimateur θ̂nB (voir l’équation (10)). La normalité asymptotique de θ̂n (Tn ) = θ̂nB énoncée
ci-dessous est une conséquence directe du Théorème 6.
d
1/2
1/2
(1)
satisfaites. Si kn b(log(n/kn )) → 0 et log(kn )/ log(n) → 0 alors kn (θ̂n (Tn )−θ ) → N (0, θ 2 ).
Dans le Corollaire 1 du sous-paragraphe précédent, ce résultat est obtenu sous la condition sup1/2
plémentaire kn / log(n) → 0.
Un choix naturel pour (Tn ) est de prendre la suite annulant une partie du biais asymptotique :
(2)
la partie dépendant de un . Pour ce faire, il suffit de prendre (Tn ) = (Tn ) avec
Z ∞
x
(2)
e−x dx.
Tn = kn
log 1 +
log(n/k
)
0
n
(2)
En remarquant que Tn = n/kn E1 (log(n/kn )), où E1 (z) dénote l’exponentielle intégrale calculée
(2)
au point z (voir (Abramowitz and Stegan, 1972, Chapitre 5, p. 225-233)), le calcul de la suite Tn
est simple à effectuer. Il est aussi intéressant de noter que
(1)
Tn
kn
log(i/kn )
= ∑ log 1 −
log(n/kn )
i=1
(2)
est en fait l’approximation par des sommes de Riemann de Tn car en intégrant par partie on
montre que
Z 1
log(x)
(2)
Tn =
log 1 −
dx.
log(n/kn )
0
On déduit du Théorème 6 le résultat suivant :
d
1/2
1/2
(2)
satisfaites. Si kn b(log(n/kn )) → 0 alors kn (θ̂n (Tn ) − θ ) → N (0, θ 2 ).
Une des hypothèses du Théorème 6 étant que Tn kn log(n/kn ) → 1, un choix simple est de
(3)
prendre Tn = Tn = (kn log(n/kn ))−1 . La normalité asymptotique de l’estimateur ainsi obtenu est
donnée ci-dessous :
d
1/2
1/2
1/2
(3)
satisfaites. Si kn b(log(n/kn )) → 0 et kn / log(n/kn ) → 0 alors kn (θ̂n (Tn ) − θ ) → N (0, θ 2 ).
Notez que les Corollaires 3, 4 et 5 sont énoncés dans (Gardes and Girard, 2006, Corollaire 1) et
sont démontrés dans ce même article. Nous allons à présent comparer ces trois estimateurs en
fonction de leur erreur moyenne quadratique asymptotique définie par l’équation (15).
109
Proposition 1. On se place sous le modèle (8) et on suppose que les conditions (H.1) et (H.2)
1/2
sont satisfaites. Si kn b(log(n/kn )) → Λ ∈ R, plusieurs situations sont possibles. On pose :
β1 = 2 lim xb(x) et β2 = −4 lim b(log n)
x→∞
n→∞
kn
.
log kn
i) Soit b(.) est asymptotiquement strictement positive.
Si β1 > θ alors, pour n assez grand,
(3)
(2)
(1)
AMSE(θ̂n (Tn )) < AMSE(θ̂n (Tn )) < AMSE(θ̂n (Tn )).
Si β1 < θ alors, pour n assez grand,
(2)
(1)
(3)
AMSE(θ̂n (Tn )) < min(AMSE(θ̂n (Tn )), AMSE(θ̂n (Tn ))).
ii) Soit b(.) est asymptotiquement strictement négative.
Si β2 > θ , alors, pour n assez grand,
(1)
(2)
(3)
AMSE(θ̂n (Tn )) < AMSE(θ̂n (Tn )) < AMSE(θ̂n (Tn )).
Si β2 < θ , alors, pour n assez grand,
(2)
(1)
(3)
AMSE(θ̂n (Tn )) < min(AMSE(θ̂n (Tn )), AMSE(θ̂n (Tn ))).
Cette proposition a été établie dans (Gardes and Girard, 2006, Théorème 3). Comme l’on pouvait
s’y attendre, il n’y a pas d’estimateur qui soit préférable dans toutes les situations. Dans le
(1)
cas i), β1 ne dépend pas de la suite (kn ). Le classement entre les trois estimateurs θ̂n (Tn ),
(2)
(3)
θ̂n (Tn ) et θ̂n (Tn ) dépend donc uniquement de la loi des observations. Si la fonction biais
(2)
b(.) converge rapidement vers zéro alors β1 < θ et ainsi l’utilisation de l’estimateur θ̂n (Tn ) est
(3)
préférable. Au contraire, si b(.) converge lentement vers zéro, β1 > θ et l’estimateur θ̂n (Tn )
sera de meilleure qualité. Dans le cas ii), β2 dépend de la suite (kn ). Si (kn ) est petite (par exemple
(2)
kn ∝ −1/b(log(n))) alors β2 = 0 et l’estimateur θ̂n (Tn ) est préférable. Inversement, si (kn ) est
(1)
grande (par exemple kn ∝ (b(log(n)))−2 ) alors β2 = ∞ et θ̂n (Tn ) sera asymptotiquement le
meilleur estimateur. Enfin, si β1 = θ , on ne peut pas comparer dans la situation i) les estimateurs
(2)
(3)
(3)
(2)
θ̂n (Tn ) et θ̂n (Tn ) car AMSE(θ̂n (Tn )) − AMSE(θ̂n (Tn )) → 0 lorsque n tend vers l’infini. De
(1)
(2)
même, dans la situation ii), on ne peut pas comparer les estimateurs θ̂n (Tn ) et θ̂n (Tn ) si β2 = θ .
Les comparaisons ci-dessus sont uniquement valables asymptotiquement. Afin de voir si elles
sont aussi valides pour une taille d’échantillon finie, nous simulons N = 200 échantillons de taille
(1)
n = 500 d’une loi Γ(0.5, 1). Pour chaque échantillon, nous calculons les estimateurs θ̂n,i (Tn ),
(2)
(3)
θ̂n,i (Tn ) et θ̂n,i (Tn ) (i = 1, . . . , N) pour différentes valeurs de kn . Nous en déduisons les erreurs
en moyenne quadratique empiriques définies par :
1 N
( j)
(θ̂n,i (Tn ) − θ )2 , j = 1, 2, 3.
∑
N i=1
110
Ces erreurs empiriques sont comparées aux erreurs asymptotiques des trois estimateurs données
par l’équation (15). Les résultats sont présentés dans la Figure 2 où l’on s’aperçoit que le
comportement des erreurs empiriques et celui des erreurs asymptotiques sont très similaires. Les
résultats de comparaison des trois estimateurs données dans le Théorème 1 semblent donc aussi
utilisables pour une taille d’échantillon finie. D’autres simulations avec différentes lois ont été
faites (voir Gardes and Girard (2006)) conduisant à la même conclusion.
3.1.3. Un estimateur de θ débiaisé
Considérons à présent un estimateur débiaisé de l’indice de queue de Weibull θ . Il est basé sur
un modèle de régression exponentiel inspiré de ceux proposés par Beirlant et al. (1999, 2002) et
Feuerverger and Hall (1999) afin d’estimer l’indice des valeurs extrêmes pour des lois du domaine
d’attraction de Fréchet. Plus précisément, on définit les variables aléatoires
Z j = j log(n/ j)(log(Xn− j+1,n ) − log(Xn− j,n )), j = 1, . . . , kn .
Le modèle suivant peut être établi (Diebolt et al., 2008a, Corollaire 2.1) :
log(n/kn )
b(log(n/kn )) f j + oP (b(log(n/kn ))), j = 1, . . . , kn
Zj = θ +
log(n/ j)
(16)
où f j , j = 1, . . . , kn sont des variables aléatoires indépendantes de loi exponentielle de paramètre 1 et le terme oP (b(log(n/kn ))) ne dépend pas de j. On obtient à partir du modèle (16)
l’approximation
Z j ≈ θ + b(log(n/kn ))x j + η j , j = 1, . . . , kn
(17)
où η j est un terme d’erreur aléatoire centré et x j = log(n/kn )/ log(n/ j). En estimant les paramètres θ et b(log(n/kn )) du modèle de régression linéaire (17) par la méthode des moindres
carrés ordinaires, on obtient un estimateur de θ débiaisé :
θ̂nD =
1
kn
kn
∑ Zj −
j=1
b̂(log(n/kn ))
kn
kn
∑ x j,
(18)
j=1
où
kn
b̂(log(n/kn )) =
∑
j=1
1
xj −
kn
kn
∑ xj
j=1
!
,
Zj
kn
∑
j=1
1
xj −
kn
kn
∑ xj
!2
.
(19)
j=1
La normalité asymptotique de θ̂nD est donnée par le résultat ci-dessous (voir (Diebolt et al., 2008a,
Théorème 3.1)).
satisfaites. Supposons de plus que la fonction b(.) est telle que x|b(x)| → ∞ lorsque x → ∞ avec
1/2
kn
b(log(n/kn )) → Λ̃ ∈ R.
log(n/kn )
111
1/2
log2 (kn )
kn
Supposons enfin que, si Λ̃ = 0,
→ 0 et
→ ∞. On a :
log(n/kn )
log(n/kn )
1/2
kn
d
(θ̂ D − θ ) → N (0, θ 2 ).
log(n/kn ) n
L’hypothèse x|b(x)| → ∞ implique que dans la condition (H.2) la vitesse de convergence est lente
(et plus particulièrement que ρ ≥ −1). Les estimateurs non débiaisés de θ auront donc tendance à
avoir un biais important dans ce cas. On peut montrer (voir Table 2) que les lois normale, Gamma
satisfont cette hypothèse mais pas les lois de Weibull. En prenant Λ 6= 0 dans les Théorèmes 5
et 6 et Λ̃ 6= 0 dans le Théorème 7, on montre que l’estimateur débiaisé θ̂nD (voir l’équation (18))
admet la même vitesse de convergence que les estimateurs des familles Θ1 et Θ2 avec en plus un
biais asymptotique nul.
3.1.4. Illustration sur simulations
Nous effectuons une simulation afin de comparer le comportement de l’estimateur non débiaisé
θ̂nB (voir l’équation (10)) avec celui de l’estimateur débiaisé θ̂nD (voir l’équation (18)). Nous
générons N = 100 échantillons de taille n = 500 selon une loi normale centrée et réduite (pour
laquelle θ = 1/2). En fonction du nombre de statistiques ordonnées kn , nous comparons sur
la Figure 3 les moyennes empiriques des deux estimateurs ainsi que leurs erreurs moyennes
quadratiques empiriques. Nous notons un bon comportement de l’estimateur débiaisé en terme
de biais ainsi qu’en terme de variance. La méthode de débiaisage proposée semble donc efficace
à taille d’échantillon finie. Des simulations sur d’autres lois ont confirmé ce bon comportement
(voir (Diebolt et al., 2008a, Section 4)).
3.1.5. Choix du nombre kn de statistiques d’ordre
En ne tenant pas compte du terme de biais dans le modèle de régression (16), on obtient un
estimateur non débiaisé de θ défini par :
1
kn
kn
∑ Z j.
j=1
L’erreur moyenne quadratique asymptotique (AMSE) de cet estimateur est donnée par (Diebolt
et al., 2008a, Théorème 2.2) :
!2
θ2
b(log(n/kn )) kn log(n/kn )
+
AMSE(kn ) =
.
∑
kn
kn
j=1 log(n/ j)
Un choix possible pour kn est alors de prendre knopt = arg minkn AMSE(kn ). Nous pouvons estimer
\ n ) obtenue en remplaçant θ et b(log(n/kn ) par les estimateurs
cette erreur par la quantité AMSE(k
D
θ̂n et b̂(log(n/kn ) définis précédemment (voir les équations (18) et (19)). Le nombre knopt est
estimé par :
\ n ).
k̂n = arg min AMSE(k
kn
112
AMSE
MSE
0.00
0.05
0.10
0.15
0.20
0.00
0.25
0.05
0.10
0.15
0.20
0.25
0
0
50
50
100
k
k
150
100
200
150
250
(1)
(2)
(3)
F IGURE 2. Comparaison des estimateurs θ̂n (Tn ) (trait plein), θ̂n (Tn ) (tirés) et θ̂n (Tn ) (pointillés). En abscisse,
kn et en ordonnée les erreurs moyenne quadratique empiriques (gauche) et asymptotiques (droite).
F IGURE 3. Comparaison des estimateurs θ̂nD (×) et θ̂nB (). En abscisse, kn et en ordonnée les erreurs en moyenne
quadratique empiriques (gauche) et asymptotiques (droite).
113
Comme l’ont fait remarquer récemment Asimit et al. (2010), AMSE(kn ) ∼ θ 2 /kn + b2 (log(n)).
Ainsi, la sélection du nombre d’observations kn n’est pas justifiée théoriquement puisque knopt ∼ n.
Cependant, les simulations effectuées dans (Diebolt et al., 2008a, Section 4) montrent que
l’utilisation de la valeur k̂n pour estimer l’indice θ conduit à de bons résultats. Une méthode
alternative a récemment été proposée Mercadier and Soulier (2011) basée sur les idées de Drees
and Kaufmann (1998) elles-mêmes inspirées d’une variante de la méthode de Lepski et al. (1997).
3.2. Estimation de quantiles extrêmes
Toujours pour des lois à queue de type Weibull, nous nous intéressons à présent au problème
d’estimation d’un quantile extrême q(αn ) lorsque l’ordre αn converge vers zéro. Le principal
estimateur de q(αn ) disponible dans la littérature a été proposé par Beirlant et al. (1996). Il est
basé sur l’approximation (11) qui assure que pour n assez grand, on a sous l’hypothèse (H.1) :
log q(αn ) ≈ θ log log(1/αn ) et log q(kn /n) ≈ θ log log(n/kn ).
En soustrayant membre à membre les deux approximations ci-dessus et en appliquant la fonction
exponentielle, on montre facilement que :
log(1/αn )
q(αn ) ≈ q(kn /n)
log(n/kn )
θ
.
En estimant q(kn /n) par Xn−kn +1,n qui est le quantile associé à la fonction de répartition empirique
et θ par θ̂nB (voir équation (10)), Beirlant et al. (1996) proposent l’estimateur suivant :
B
q̂ (αn ) = Xn−kn +1,n
log(1/αn )
log(n/kn )
θ̂nB
.
La construction de cet estimateur est similaire à celle de l’estimateur proposé par Weissman
(1978) (voir équation (4)) pour des lois du domaine d’attraction de Fréchet. Un autre estimateur
de q(αn ) a été proposé par Beirlant et al. (1995). Il est défini par :
B∗
q̂ (αn ) = Xn−kn +1,n
σ̂n log(kn /(nαn ))
1+
θ̂nB∗ Xn−kn +1,n
!θ̂nB∗
,
avec
σ̂n =
log n/kn
1 kn −1
∑ (Xn−i+1,n − Xn−kn +1,n ) et θ̂nB∗ = Xn−k +1,n σ̂n .
kn − 1 i=1
n
Etant donné que
1+
σ̂n log(kn /(nαn )) log(1/αn )
,
=
log(n/kn )
θ̂nB∗ Xn−kn +1,n
l’estimateur q̂B∗ (αn ) est en fait l’estimateur q̂B (αn ) pour lequel l’indice θ n’est pas estimé par
θ̂nB mais par θ̂nB∗ . L’étude du comportement asymptotique de ces deux estimateurs peut alors être
114
unifiée Gardes and Girard (2005). Plus généralement, intéressons-nous à la famille d’estimateurs
du quantile extrême q(αn ) définie par
Qαn = {q̂(αn , θ̂n ), θ̂n estimateur de θ },
avec
q̂(αn , θ̂n ) = Xn−kn +1,n τnθ̂n , τn =
log(1/αn )
,
log(n/kn )
(20)
où θ̂n est un estimateur quelconque de θ .
3.2.1. Etude de la famille d’estimateurs Qαn
Nous nous proposons d’établir la loi asymptotique des estimateurs de la famille Qαn . Deux
situations peuvent se présenter : soit l’estimateur θ̂n converge rapidement vers θ de telle sorte
que la loi asymptotique de q̂(αn , θ̂n ) est donnée par celle de la statistique d’ordre Xn−kn +1,n . Cette
situation se présente lorsque la condition ci-dessous est satisfaite :
P
1/2
(H.5) Il existe une suite βn telle que log(n/kn )kn (θ̂n − βn − θ ) → 0.
1/2
Soit la vitesse de convergence de θ̂n vers θ est inférieure à log(n/kn )kn et dans ce cas la loi
asymptotique est celle de l’estimateur de l’indice θ . Cette situation est décrite par la condition
(H.6) Il existe deux suites ϑn et βn ainsi qu’une loi non dégénérée D telles que :
d
1/2
ϑn = o(log(n/kn )kn ) et ϑn (θ̂n − βn − θ ) → D.
Dans les deux situations, la suite (βn ) représente le biais asymptotique de l’estimateur de l’indice θ .
Le théorème suivant établit la loi asymptotique des estimateurs de la famille {q̂(αn , θ̂n )} dans les
deux situations décrites ci-dessus. Ce résultat est énoncé et démontré dans (Gardes and Girard,
2005, Théorème 2).
satisfaites. Si τn → τ ∈]1, ∞[ alors :
1/2
• sous la condition (H.5) et si kn log(n/kn )b(log(n/kn )) → 0,
1/2
log(n/kn )kn τ −βn
q̂(αn , θ̂n )
− τnβn
q(αn )
!
d
→ N (0, θ 2 ).
• sous la condition (H.6) et si ϑn b(log(n/kn )) → 0,
ϑn −βn
τ
log(τ)
q̂(αn , θ̂n )
− τnβn
q(αn )
!
d
→ D.
115
Le meilleur estimateur du quantile extrême q(αn ) est obtenu en utilisant un estimateur de θ satisfaisant l’hypothèse (H.5) avec βn = 0. Malheureusement, à notre connaissance, un tel estimateur
de θ n’existe pas. A titre d’exemple, l’estimateur de θ proposé par Broniatowski (1993) satisfait
la condition (H.5) mais avec un biais asymptotique βn non nul. Pour la grande majorité des
estimateurs de l’indice θ (notamment ceux introduits dans le paragraphe 3.1), c’est la condition
(H.6) qui est satisfaite avec un biais asymptotique pouvant être annulé.
La condition τn → τ ∈]1, ∞[ implique que l’on peut choisir un ordre αn proportionnel à n−τ . Ainsi,
plus τ est grand plus le quantile estimable est extrême. En contre partie, une grande valeur de τ
augmente la variance asymptotique de l’estimateur dans les deux situations.
On peut montrer que lorsque la condition (H.6) est satisfaite avec un biais asymptotique βn = 0, la
vitesse de convergence de q̂(αn , θ̂n ) est de l’ordre de (log(n))−ρ−ε où ε ∈]0, −ρ[ peut être choisi
aussi petit que l’on veut.
3.2.2. Un estimateur de q(αn ) débiaisé
Pour proposer un estimateur débiaisé du quantile extrême q(αn ), on se base sur le résultat suivant
établi dans Diebolt et al. (2008b) : sous la condition (H.2), si τn → τ ∈]1, ∞[, on a lorsque n → ∞
q(αn ) ∼ q(kn /n)τnθ exp{b(log(n/kn ))Kρ (τn )}.
En estimant q(kn /n) par la statistique d’ordre Xn−kn +1,n , θ par θ̂nD (voir équation (18)), b(log(n/kn ))
par b̂(log(n/kn )) (voir équation (19)) et ρ par un estimateur ρ̂n , on obtient l’estimateur
θ̂ D
Xn−kn +1,n τn n exp{b̂(log(n/kn ))Kρ̂n (τn )}.
Si on néglige le terme de correction exp{b̂(log(n/kn ))Kρ̂n (τn )} dans l’expression ci-dessus, on
retrouve l’estimateur non débiaisé q̂(αn , θ̂nD ) appartenant à la famille Qαn (voir équation (20)).
Concernant le paramètre ρ, plusieurs estimateurs ont été proposés pour des modèles différents
(citons les travaux de Gomes (2002), Gomes et al. (2007), Feuerverger and Hall (1999), Peng
and Yongcheng (2004) et Beirlant et al. (1999)). Le résultat suivant (voir (Diebolt et al., 2008b,
Théorème 1)), montre que l’on peut remplacer ρ̂n par une valeur arbitraire ρ \ < 0 et obtenir un
estimateur
θ̂ D
q̂D (αn ) = Xn−kn +1,n τn n exp{b̂(log(n/kn ))Kρ \ (τn )}
asymtotiquement normal.
satisfaites. Supposons que la fonction b(.) est telle que x|b(x)| → ∞ lorsque x → ∞ avec
1/2
kn
b(log(n/kn )) → Λ̃ ∈ R.
log(n/kn )
1/2
log2 (kn )
kn
Supposons de plus que, si Λ̃ = 0,
→ 0 et
→ ∞. Alors, si τn → τ ∈]1, ∞[ on
log(n/kn )
log(n/kn )
a:
D
1/2
kn
q̂ (αn )
d
− 1 → N (Λ̃µ(τ), θ 2 σ 2 (τ)),
log(n/kn ) q(αn )
avec σ 2 (τ) = (Kρ \ (τ) − log(τ))2 et µ(τ) = (Kρ \ (τ) − Kρ (τ))2 .
116
Si Λ̃ 6= 0 et si ρ \ = ρ alors l’estimateur q̂D (αn ) est sans biais avec une vitesse de convergence
\
de l’ordre de log−ρ (n)`∗ (log(n)) où `∗ (.) est une fonction à variations lentes. Cette vitesse est
meilleure que celle obtenue pour les estimateurs de la famille Qαn lorsque θ̂n satisfait l’hypothèse
(H.6) avec un biais asymptotique βn = 0. Evidemment un mauvais choix de ρ \ conduit à un
estimateur du quantile extrême biaisé. Notons cependant que les lois à queue de type Weibull
usuelles (loi normale, Gamma) ont un paramètre du second ordre ρ = −1. En pratique, on prendra
donc une valeur ρ \ égale à −1.
4. Pour aller plus loin
Dans cet article, nous nous sommes intéressés à la famille des lois à queue de type Weibull.
Ce type de lois interviennent dans de nombreuses applications (hydrologie notamment), des
publications récentes leur sont consacrées. Citons par exemple Dierckx et al. (2009) qui utilisent
la moyenne des excès au-dessus d’un seuil pour estimer l’indice de queue de Weibull et Goegebeur
and Guillou (2010) qui proposent des tests d’adéquation pour ces types de lois.
Nous avons étudié plusieurs estimateurs de l’indice de queue et de quantiles extrêmes. On
aura pu remarquer la grande similarité entre les estimateurs de l’indice de queue de Weibull
(équation (10) par exemple) avec l’estimateur de Hill (3) dédié à l’indice des valeurs extrêmes
dans le cas de lois à queues lourdes. Pour expliquer ce phénomène, une famille de lois englobant
notamment les lois du domaine d’attraction de Fréchet et les lois à queue de type Weibull a été
introduite récemment Gardes et al. (2011). La fonction de survie de ces lois est donnée par
F̄(x) = exp −Kτ−1 (log(x1/θ `(x)) ,
(21)
où θ > 0, `(.) est une fonction à variations lentes et on rappelle que
Z x
Kτ (x) =
uτ−1 du, τ ∈ [0, 1].
1
Ainsi, si τ = 0, F̄(.) est la fonction de survie d’une loi à queue de type Weibull d’indice θ . Si
τ = 1, la fonction de survie est celle d’une loi du domaine d’attraction de Fréchet avec pour indice
des valeurs extrêmes θ . Les valeurs intermédiaires de τ permettent d’inclure par exemple la loi
lognormale.
Si τ est connu, le paramètre θ du modèle (21) est estimé par
θ̌n =
1 kn −1
1
∑ (log(Xn−i+1,n ) − log(Xn−kn +1,n )),
µ1,τ (log(n/kn )) kn − 1 i=1
avec pour t > 0,
Z ∞
µ1,τ (t) =
0
(Kτ (x + t) − Kτ (t)) e−x dx.
La normalité asymptotique de cet estimateur est établie dans (Gardes et al., 2011, Théorème
1). On retrouve comme cas particuliers les résultats de normalité de l’estimateur de l’indice des
valeurs extrêmes proposé par Hill (1975) et l’estimateur de l’indice de queue de Weibull proposé
par Beirlant et al. (1996). Un estimateur des quantiles extrêmes est également introduit :
q̌n (αn ) = Xn−kn +1,n exp θ̌n [Kτ (log(1/αn )) − Kτ (log(n/kn ))] .
117
et sa normalité asymptotique est établie dans (Gardes et al., 2011, Théorème 2). En pratique, le
paramètre τ est inconnu. Un estimateur est proposé dans Methni et al. (2012). Ses propriétés
asymptotiques sont établies ainsi que les conséquences de son estimation sur la loi limite des
estimateurs θ̌n et q̌n (αn ). Ces travaux ouvrent la porte à la construction de tests d’hypothèses pour
les queues de distributions. Pour un jeu de données réelles, on pourrait notamment décider s’il est
issu d’une loi à queue lourde ou d’une loi à queue de type Weibull.
Références
Abramowitz, M. and Stegan, J. (1972). Handbook of Mathematical Functions with Formulas, Graphs and Mathematical
Tables. Dover, New York.
Asimit, V., Li, D., and Peng, L. (2010). Pitfalls in using Weibull tailed distributions. Journal of Statistical Planning
and Inference, 140 :2018–2024.
Beirlant, J., Bouquiaux, C., and Werker, B. (2006). Semiparametric lower bounds for tail index estimation. Journal of
Statistical Planning and Inference, 136 :705–729.
Beirlant, J., Broniatowski, M., Teugels, J., and Vynckier, P. (1995). The mean residual life function at great age :
applications to tail estimation. Journal of Statistical Planning and Inference, 45 :21–48.
Beirlant, J., Dierckx, G., Goegebeur, Y., and Matthys, G. (1999). Tail index estimation and an exponential regression
model. Extremes, 2 :177–200.
Beirlant, J., Dierckx, G., Guillou, A., and Stǎricǎ, C. (2002). On exponential representations of log-spacings of extreme
order statistics. Extremes, 5 :157–180.
Beirlant, J. and Teugels, J. (1992). Modelling large claims in non-life insurance. Insurance : Mathematics and
Economics, 11 :17–29.
Beirlant, J., Teugels, J., and Vynckier, P. (1996). Practical analysis of extreme values. Leuven University Press,
Leuven, Belgium.
Berred, M. (1991). Record values and the estimation of the Weibull tail-coefficient. Comptes-Rendus de l’Académie
des Sciences, T. 312, Série I :943–946.
Bingham, N., Goldie, C., and Teugels, J. (1987). Regular Variation. Cambridge University Press.
Brodin, E. and Rootzén, H. (2009). Univariate and bivariate gpd methods for predicting extreme wind storm losses.
Insurance : Mathematics and Economics, 44 :345–356.
Broniatowski, M. (1993). On the estimation of the Weibull tail coefficient. Journal of Statistical Planning and
Inference, 35 :349–366.
Csörgő, S., Deheuvels, P., and Mason, D. (1985). Kernel estimates of the tail index of a distribution. The Annals of
Statistics, 13 :1050–1077.
Csörgő, S. and Viharos, L. (1998). Estimating the tail index. In Szyszkowicz, B., editor, Asymptotic Methods in
Probability and Statistics, pages 833–881. TEST, North-Holland, Amsterdam.
de Haan, L. and Ferreira, A. (2006). Extreme value theory : an introduction. Springer.
Diebolt, J., Gardes, L., Girard, S., and Guillou, A. (2008a). Bias-reduced estimators of the Weibull tail-coefficient.
Test, 17 :311–331.
Diebolt, J., Gardes, L., Girard, S., and Guillou, A. (2008b). Bias-reduced extreme quantiles estimators of Weibull
tail-distributions. Journal of Statistical Planning and Inference, 138 :1389–1401.
Dierckx, G., Beirlant, J., Waal, D. D., and Guillou, A. (2009). A new estimation method for Weibull-type tails based
on the mean excess function. Journal of Statistical Planning and Inference, 139(6) :1905–1920.
Ditlevsen, O. (1998). Distribution arbitrariness in structural reliability. In Balkema, editor, Structural Safety and
Reliability, pages 1241–1247. TEST, Rotterdam.
Drees, H. and Kaufmann, E. (1998). Selecting the optimal sample fraction in univariate extreme value estimation.
Stochastic process and Application, 75 :149–172.
Embrechts, P., Klüppelberg, C., and Mikosch, T. (1997). Modelling extremal events. Springer.
Falk, M. (1995). Some best parameter estimates for distributions with finite endpoint. Statistics, 27 :115–125.
Falk, M. and Marohn, F. (1997). Efficient estimation of the shape parameter in Pareto models with partially known
scale. Statistics & Decisions, 15 :229–239.
118
Feuerverger, A. and Hall, P. (1999). Estimating a tail exponent by modelling departure from a Pareto distribution. The
Annals of Statistics, 27 :760–781.
Gardes, L. and Girard, S. (2005). Estimating extreme quantiles of Weibull tail-distributions. Communication in
Statistics - Theory and Methods, 34 :1065–1080.
Gardes, L. and Girard, S. (2006). Comparison of Weibull tail-coefficient estimators. REVSTAT - Statistical Journal,
4(2) :163–188.
Gardes, L. and Girard, S. (2008). Estimation of the Weibull tail-coefficient with linear combination of upper order
statistics. Journal of Statistical Planning and Inference, 138 :1416–1427.
Gardes, L., Girard, S., and Guillou, A. (2011). Weibull tail-distributions revisited : a new look at some tail estimators.
Journal of Statistical Planning and Inference, 141(1) :429–444.
Geluk, J. and Haan, L. D. (1987). Regular variation, extensions and Tauberian theorems. Center for Mathematics and
Computer Science, Amsterdam, Netherlands.
Girard, S. (2004). A Hill type estimate of the Weibull tail-coefficient. Communication in Statistics - Theory and
Methods, 33(2) :205–234.
Girard, S., Guillou, A., and Stupfler, G. (2012). Estimating an endpoint with high order moments in the Weibull
domain of attraction. Statistics and Probability Letters, 82 :2136–2144.
Gnedenko, B. (1943). Sur la distribution limite du terme maximum d’une série aléatoire. The Annals of Mathematics,
44 :423–453.
Goegebeur, Y., Beirlant, J., and de Wet, T. (2010). Generalized kernel estimators for the Weibull-tail coefficient.
Communications in Statistics - Theory and Methods, 39(20) :3695–3716.
Goegebeur, Y. and Guillou, A. (2010). Goodness-of-fit testing for Weibull-type behavior. Journal of Statistical
Planning and Inference, 140(6) :1417–1436.
Gomes, M. (2002). Asymptotic unbiased estimators of the tail index based on external estimation of the second order
parameter. Extremes, 5(1) :5–31.
Gomes, M., Martins, M., and Neves, M. (2007). Improving second order reduced bias extreme value index estimation.
REVSTAT - Statistical Journal, 5(2) :177–207.
Hall, P. and Park, B. (2002). New methods for bias correction at endpoints and boundaries. The Annals of Statistics,
30(5) :1460–1479.
Hill, B. (1975). A simple general approach to inference about the tail of a distribution. The Annals of Statistics,
3 :1163–1174.
Kratz, M. and Resnick, S. (1996). The qq-estimator and heavy tails. Stochastic Models, 12 :699–724.
Lepski, O., Mammen, E., and Spokoiny, V. (1997). Optimal spatial adaption to inhomogeneous smoothness : an
approach based on kernel estimates with variable bandwidth selectors. The Annals of Statistics, 25 :929–947.
Mason, D. (1981). Asymptotic normality of linear combinations of order statistics with a smooth score function. The
Annals of Statistics, 9(4) :899–908.
Mercadier, C. and Soulier, P. (2011). Optimal rates of convergence in the Weibull model based on kernel-type
estimators. Statistics and Probability Letters, 82 :548–556.
Methni, J. E., Gardes, L., Girard, S., and Guillou, A. (2012). Estimation of extreme quantiles from heavy and light
tailed distributions. Journal of Statistical Planning and Inference, 142(10) :2735–2747.
Peng, L. and Yongcheng, Q. (2004). Estimating the first and second order parameters of a heavy tailed distribution.
Australian and New Zealand Journal of Statistics, 46(2) :305–312.
Resnick, S. (1987). Extreme values, regular variation and point processes. Springer Series in Operations Research and
Financial Engineering.
Rootzén, H. and Tajvidi, T. (2001). Can losses caused by wind storms be predicted from meteorological observations ?
Scandinavian Actuarial Journal, 5 :162–175.
Schultze, J. and Steinebach, J. (1996). On least squares estimates of an exponential tail coefficient. Statistics and
Decisions, 14 :353–372.
Weissman, I. (1978). Estimation of parameters and large quantiles based on the k largest observations. Journal of the
American Statistical Association, 73 :812–815.

Estimation de quantiles extrêmes pour les lois à queue de type

Transcription

Documents pareils

Rapide utilisation de visualroute

SEND LOG FILES → ENVOYER UN FICHIER LOG 1) Connectez

Régression non paramétrique sur l`hyper

Suivi de production

d`où log tang-C

Transformateur de log

CLUB LOG 2015 infos - club logistique et transport 59

Recopie du fichier log

Solutions