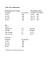contrôle de gestion

Notes de cours d’étudiants
Selon l’intitulé :
« CONTRÔLE DE GESTION »
Prof. B. MORARD
Notes originales fournies par :
NOM
PRENOM
ANNEE
KRIVOBOK
KAROLINKA
2011-2012
PRENOM
ANNEE
Dernière mise à jours par :
NOM
Avertissements : Le présent document regroupe des notes d’étudiants relatives au cours nommé cidessus. Il est mis gratuitement à disposition des étudiants par le CHEC ; son contenu ne peut en
aucun cas être vendu.
De plus, ce document n’est pas un polycopié officiel : son contenu n’est pas garanti, il ne dispense
donc pas d’être présent aux cours.
Enfin, quiconque bénéficie du présent support se doit de le mettre à jours en corrigeant les
éventuelles erreurs et en le complétant (merci de renvoyer les documents modifiés à l’adresse
[email protected])
Introduction
La problématique du contrôle de gestion :
On a l’habitude de justifier le contrôle de gestion en partant de l’analyse stratégique. En effet une
entreprise peut dominer un marché à partir de 3 stratégies :
-
Stratégie de coûts : je suis capable de mettre un produit au cout le plus bas. (celle qui nous
intéresse le plus)
-
Stratégie de différenciation : j’ai un + par rapport aux autres. On se sert d’avantages
compétitifs, tel que la réputation du produit.
-
Stratégie de réseaux : question de différenciation et de domination par les coûts, tel que
l’économie d’échelles (en gros un mélange des deux ci-dessus). Par ex. : Benetton n’a
presque que des franchises, ils organisent la pub et la production, mais n’ont aucune
productions propres.
Le second élément avec la stratégie, concerne la mondialisation où la concurrence s’intensifie pour
acquérir des ressources rares et il faut donc savoir de quelles façons ces ressources vont être
consommées. Enfin le 3ème élément concerne les propriétaires actionnaires de l’entreprise qui
veulent plus d’informations opérationnelles.
La notion de prix de revient ou de coût de revient n’existe que dans un environnement concurrentiel
où offre et demande s’exprime librement. Sur ces marchés concurrentiels, l’entreprise subit la loi du
marché et n’a aucun impact sur le prix de vente, elle ne peut agir que sur la combinaison de
production, c’est-à-dire la combinaison capital/travail et essayer de l’optimiser pour avoir le coût de
production le plus bas.
Audit comptable
Audit intégré
Le processus du contrôle de gestion se décompose en 3 phases :
-
Phase 1 : on définit les budgets à partir des coûts, des prix et des quantités. Ce budget peut
être exprimé en termes physiques ou financiers.
-
Phase 2 : l’exercice budgétaire a commencé, on va alors procéder au contrôle de conformité :
analyser les pièces comptables pour savoir si les procédures d’engagements ont été
respectées.
-
Phase 3 : on va procéder à l’analyse de la performance, comparer le budget aux charges
réelles et procéder à l’analyse des écarts.
En général le budget porte sur un horizon d’une année. En fin de période on procède à l’analyse des
écarts et on recommence l’exercice budgétaire. Un auditeur comptable va s’occuper des 2 premières
phases, tandis qu’un auditeur intégré va s’occuper des 3 phases.
Les conceptions du contrôle de gestion ont évolué par 3 phases successives :
•
•
•
une phase purement comptable où on s’intéressait à l’aspect mécanique du prix de revient.
On parlera de :

Direct Costing

Sections Homogènes

Standard
à cela succède la vision de l’ingénieur où l’on a essayé d’améliorer et de rationnaliser les
processus de production. On parlera ici de :
o
Target Costing
o
Kaizen Costing
Enfin la phase actuelle met l’accent sur les méthodes d’organisation et la gestion de la
performance.
L’information comptable se divise en 2 catégories : la comptabilité financière et la comptabilité de
gestion ou analytique.
Dans la compta financière : nous faisons référence au bilan et au compte de résultat.
Dans la compta de gestion : nous faisons référence aux coûts et aux prix de revient des produits et
des services. De fait, dans la compta générale les charges sont classées par natures alors que dans la
compta analytique on va vouloir classer ces charges par objets, qu’il s’agisse de coûts de
département ou de coûts de produits finaux. On doit se poser la question : « Quel produit ou quel
département a consommé quel ressources ? ».
Bilan  Décrit la richesse de l’entreprise, sa position patrimoniale. C’est une compta en termes de
stock.
Compte de résultat compta en termes de flux, retrace ce qu’il s’est passé dans l’entreprise, ses
dépenses et ses recettes faites durant l’année.
Un coût est :
Une charge physique ou financière que l’on va attacher à une structure intermédiaire appelée
département, à des produits finaux ou à des services. En effet le coût d’un produit peut être exprimé
en terme monétaire, il peut aussi être exprimé en consommation de facteurs (heures travaillées et
quantités de matière 1ère). C’est donc une consommation de ressources.
En compta analytique on parlera de charges incorporables (base du coût) pour les charges jugées
raisonnables. Les charges non incorporables correspondent par exemple à des taxes qui ne restent
pas a la charge de l’organisation, dotation aux provisions (réglementées ou exceptionnelles) et
impôts sur les bénéfices.
Remarque : Le C/R est un compte hors
taxes.
Exemple :
Périodes
1
2
3
4
Total :
Charges
10
19
22
29
80
Charge 1=80 . 1818+8 = 55,384615
Produit 1
2
4
5
7
18
Produit 2
2
3
2
1
8
Charge 2=80 . 818+8 = 24,615385
Notons que 55.385 + 24.615=80 (Total des charges)
Cu1=55,38461518 = 3,07 Cu2=24,615385 8 = 3,07
L’exemple ci-dessus présente sous forme très classique la problématique du calcul du prix de revient.
En effet, nous avons ici une entreprise qui fabrique simultanément deux biens. La charge par période
intéresse donc simultanément les deux produits. On parlera ainsi d’une charge indirecte.
Sur la base de cette information, supposée exacte, et sans autres informations annexe, on utilise
classiquement la règle dite « en proportion des quantités ». Sur la base de cette répartition on
obtient des coûts unitaires qui sont strictement identiques. De fait, de par cette règle, quel que soit
la composition des deux produits, ils coutent le même montant.
En fait il s’agit là d’un phénomène d’illusion monétaire provoqué par le mécanisme de répartition. Au
passage remarquons que si on additionne les deux répartitions on retrouve exactement le montant
de la charge à répartir. Cela nous amène alors à étudier les propriétés minimales que doivent
posséder les règles de répartitions.
Toutes règles de répartitions classiques doivent posséder au minimum 3 propriétés :
•
•
Identité : charge à répartir = charge répartie.
Unicité : répartir une charge où la somme de ces composantes aboutie au même
résultat.
•
Monotonicité : idée que lorsque les quantités produites augmentent, la charge doit
augmenter (hypothèse qu’un cout unitaire ne peut pas être négatif).
Toutes les règles comptables obéissent à ces trois propriétés. Certaines règles, comme la méthode
du coût marginal, n’obéissent pas à cette propriété.
Les observations précédentes permettent quelques déductions. En particulier, l’idée suivant laquelle,
par les règles de répartition en proportions, les coûts seraient identiques en 1ère observation.
Pour discuter ce point, il convient de formaliser la question de la façon suivante. Appelons :
•
•
a1 : cout unitaire inconnu du bien 1
a2 : cout unitaire inconnu du bien 2
La règle de répartition dite en proportion des quantités, peut s’écrire sous forme d’un système
d’équation :
18.a1+8.a2 = 80
a1 = a2 -> 18 a118 = 8 a28
a2
Lieu de toutes répartitions admissible
3,07
3,07
a1
a1 =0 ; a2 =10
Notons aussi qu’une répartition qui se trouve en dehors des deux droites n’est pas admissible. Car ne
correspond pas à l’allocation total des charges, ici 80.
Toute règle de répartition peut se mettre sous la forme d’un système d’équation qui se décompose
en 2 parties : la condition d’identité comptable ( ) et le rapport existant entre les coûts unitaires ( )
En observant l’équation 2 on peut alors dire que les règles en proportions sont des règles arbitraires
car on définit a priori la relation entre les deux coûts unitaires.
Périodes
1
2
Charges
10
19
Produit 1
2
4
Produit 2
2
3
3
4
22
29
80
Total
Prix de vente
Charges directes
5
7
18
7
1,25
Calculs en proportion du CA :
Charge 1 : 80*7*1818*7+(8*3) = 67,2
Coût unitaire 1 : 67,218 = 3,7333
Charge 2 : 80*3*818*7+(8*3) = 12,8
Coût unitaire 2 : 12,88 = 1,6
Dans les règles en proportions les coûts sont identiques par unité du critère :
67,27*18 = 0,53333333
12,83*8 = 0,53333333
Calculs en proportion de la quantité :
ch (1) : 80 . 1818+8 = 55,384615
ch (2) : 80 . 818+8 = 24,615385
2
1
8
3
1
cu (1) : 55,38461518 = 3,07
cu (2) : 24,615385 8 = 3,07
Calculs en proportion des charges directes :
ch (1) : 80*1,25*1818*1,25+(8*1) = 59,02
cu (1) : 59,0218 = 3,2787
ch (2) : 80*1*818*1,25+(8*1) = 20,98
cu (2) : 20,988 = 2,6229
Identique par unité de critère :
59,021,25*18 = 2,6225
20,981*8 = 2,6225
Calculs en proportion de la marge :
ch (1) : 80*18*(7-1,25)18*7-1,25+8*(3-1) = 69,2887
ch (2) : 80*8*(3-1)18*7-1,25+8*(3-1) = 10,7112
cu (1) : 69,288718 = 3,8494
cu (2) : 10,71128 = 1,3389
Identique par unité de critère :
10,71128*(3-1) = 0,6694
69,288718*(7-1,25) = 0,6694
Système d’équation pour la règle de répartition en proportion de la quantité :
18*cu(1) + 8*cu(2) = 80
cu(1) = cu(2)
Système d’équation pour la règle de répartition en proportion du CA :
18*cu(1) + 18*cu(2) = 80
18 cu(1)18*7 = 8 cu(2)8*3
Système d’équation pour la règle de répartition en proportion de la marge :
18*cu(1) + 18*cu(2) = 80
18*cu(1)18*(7-1,25) = 8*cu(2)8*(3-1)
Système d’équation pour la règle de répartition en proportion des charges :
18*cu(1) + 18*cu(2) = 80
18*cu(1)18*1,25 = 8*cu(2)8*1
Le schéma ci-dessus permet de dégager 4 règles classiques + 2 systèmes de coûts remarquables
correspondant pour ces derniers à un système de subventionnement croisé.
D’un point de vue purement comptable toutes ces règles sont parfaitement équivalentes et il est à ce
stade absolument impossible de se donner une notion d’optimalité. On a introduit dans l’analyse la
notion de charges directes, dans une entreprise on peut avoir 4 types de charges :
•
•
•
Variables et fixes
Directes et indirectes
Ou toute combinaison des 4
Une charge est dites directe quand elle ne concerne qu’un produit ou qu’une activité et qu’elle ne
fait pas l’objet d’une répartition. Charge indirecte lorsqu’une entreprise produit simultanément
plusieurs produits différents. Quelle main d’œuvre correspond à quoi ? -> Répartition des charges.
Et toute la problématique du prix de revient consiste à se poser la question de la bonne règle de
répartition.
La segmentation charge variable - charge fixe se réfère à une activité où des charges sont fonctions
du volume de production (amortissement = charge fixe).
Pour résumer ces différents points, nous noterons que la question du prix de revient repose toute
entière sur le mécanisme de la répartition. Il est tout à fait douteux que, partant de règles arbitraires,
nous puissions obtenir un prix de revient traduisant la consommation réelle de ressources. On
aboutit alors à l’idée que l’établissement d’un prix ou d’un coût de revient peut répondre à deux
impératifs :
•
•
Soit définir les consommations au niveau des produits.
Soit envoyer une information manipulée. Les deux objectifs n’aboutissent pas
nécessairement au même résultat.
Dans le premier cas de figure, l’idée serait de définir la consommation véritable par produit. Dans le
second cas de figure, nous viserions simplement un effet de démonstration
Direct costing : méthode du coût variable
La méthode du coût variable met l’accent sur la relation vente, marge et seuil de rentabilité. L’idée
sous jacente consiste à distinguer parmi les charges, les charges variables des charges fixes. Les
charges variables sont fonctions du niveau d’activité, les charges fixes existent même si l’activité est
nulle. Il est donc rationnel d’allouer les charges variables et de ne pas allouer les charges fixes
Le schéma ci-dessus appelle quelques commentaires. Tout d’abord, il n’existe ici que deux catégories
de charges :
•
•
les charges variables.
les charges fixes.
Dans la réalité il en existe quatre catégories : charges variables directes, charges variables indirectes,
charge fixes directes et charges fixes indirectes.
Si l’on adopte ce schéma du direct costing ci-dessus, il faut supposer que dans notre organisation
nous n’avons que des charges variables directes ou que nous sommes une firme mono produit.
On remarquera ensuite que les charges fixes ne viennent pas en déduction des ventes mais de la
marge brute. Cette remarque permet alors de dire que les stocks de produits finis non vendus ne
supportent que des frais variables (frais fixes quand produits vendus) donc stocks sous évalués, donc
seconde difficulté. Enfin on remarquera que le schéma ne fait référence à aucune structure
organisationnelle. Nous avons la uniquement un jeu de compte.
Pour pallier à ces difficultés bien connues, on a mis en place une variante de la méthode de base :
Pour pallier aux déficiences du coût variable simple on introduit une variable direct costing évolué.
Dans cette variable on va segmenter les charges fixes en charges fixes directes et indirectes. Ces
charges fixes directes vont être ajoutées aux charges variables. Par différence avec le prix de vente,
on va obtenir des marges semi-brutes unitaires, qui, par sommation, aboutiront à la marge semibrute totale. En résumé nous pourrons dire que la méthode directe costing évolué sous évalue moins
les stocks de produits finis que le direct costing simple.
Exemple : soit une entreprise réalisant un CA de 500'000 Fr et fabriquant pendant cette période 1570
unités. Pendant cette même période elle supporte des frais de matières premières de 200'000, des
frais de m-o pour 175'000 fr et des frais d’amortissement pour 100’000fr. On nous informe que seuls
les frais d’amortissement sont fixes. Sur la base cette information on vous demande de calculer la
marge brute unitaire, la marge brute totale et la marge nette totale.
CA
CV
Matière 1ère
m-o
CV totale
Marge brute
CF
amortissement
Marge nette
SR : CF/marge brute unitaire
total
500000
unitaire
318,471338
200000
175000
375000
125000
127,388535
111,464968
238,853503
79,6178344
100000
25000
1256 unités
On associe la méthode du direct costing avec la notion de seuil de rentabilité. Pour cette discussion
nous allons utiliser les variables suivantes :
- p : prix de vente unitaire
- x : quantité de produit
- a : coût unitaire variable
- F : charge fixe totale
Voir démonstration 3 (dans polycop)
Le problème de cette démonstration est qu’il n’y a qu’un produit.
Avec deux produits :
-
p1 et p2 : prix de vente unitaire
a1 et a2 coût variable unitaire
x1 et x2 : quantité
F : charge fixe totale
Voir démonstration 4
La question du seuil de rentabilité dans le cas multi produit est plus compliquée. En effet on aboutit à
une équation comportant deux inconnues. On en déduit alors que nous avons une infinité de
solutions. De fait, on peut en conclure que le seuil de rentabilité multi produit n’existe pas. Pour
dépasser notre interrogation, il convient de remarquer que deux produits peuvent générer des
marges très différentes. Si l’on suppose par exemple que le produit 1 génère une marge de 1000fr et
que le produit 2 génère une marge de 1fr, un plan de production rationnelle visera à réaliser
beaucoup de produit 1 et peu de produit 2. Cette décision suppose que l’on a introduit dans notre
raisonnement un critère tel qu’on va chercher à maximiser la marge brute totale correspondant à
l’un des points de la droite. Suivant cette analyse on peut définir 3 critères de sélections :
•
•
•
La maximisation de la marge brute totale
La maximisation du CA
La minimisation du coût total
Exemple : soit une entreprise mono produit.
On nous indique que l’électricité et amortissement sont fixes. Sur la base de cette information, on
vous demande de calculer la marge brute, totale et unitaire, et la marge nette totale. Vous calculerez
le SR, et le graphique correspondant.
CA
Matière
m-o
Electricité
Amortissement
CA
CV
Matière
m-o
total
Marge brute
CF
Electricité
Amortissement
total
Marge nette
SR
1'200’000
500’000
345’000
120’000
100’000
3000 unités
total
1'200’000
unitaire
400
500’000
345’000
845’000
355’000
166,666667
115
281,666667
118,3333333
120’000
100’000
220’000
135’000
1859,1549
Etude de cas 2 : Direct Costing
postes
quantité
pv
Produit 1
15000
3
Produit 2
12000
3,5
Produit 3
10000
4
Produit 4
9700
5
Total
46700
CA
Matière 1ère
m-o
CV totale
MB
MB unitaire
45000
24089,9358
8974,35897
33064,2948
11935,7053
0,79571369
42000
19271,9486
8376,06838
27648,017
14351,983
1,19599858
40000
16059,9572
7977,20798
24037,1652
15962,8348
1,59628348
485000
15578,1585
25250,5231
40828,6816
23249,4769
2,39685329
1755000
75000
110000
CF
Electricité
Amort
CF totale
Marge nette
CF répartis sur 11250
chaque
produit
SR
14138,25126
20000
25000
45000
20500
11250
11250
11250
9406,36565
7047,62037
4693,654
Cette méthode et ses variantes présentes à la fois des inconvénients et des avantages. En termes
d’avantages nous parlerons de la simplicité des concepts utilisées, de la facilité de mise en place et
de l’élégance du concept de SR. En termes d’inconvénient, la segmentation entre frais fixes et frais
variables n’est pas évidente en pratique, la notion de marge brute ne présente de l’intérêt que dans
la mesure où les frais fixes sont proportionnellement élevés, enfin le SR n’est vraiment pertinent que
pour le cas mono produit. Au total, on peut parler d’une méthode d’un intérêt limité, très utilisée
dans tout ce qui est activité commerciale dans lequel il n’y pas de phase de transformation du
produit. On remarquera enfin que la méthode direct costing rentre dans la catégorie des méthodes
dites de coûts partiels dans lesquelles nous n’affectons qu’une partie des charges au produit. Ici, très
spécifiquement, nous n’affectons que les frais variables.
Sections homogènes : méthode des coûts complets
Contrairement à la méthode précédente, la méthode des sections homogènes est une méthode de
coûts complets dans laquelle on va affecter toutes les charges au produit pour pouvoir calculer la
profitabilité nette. De plus, on veut décrire en détail le processus de fabrication, pour cela on va
créer la notion de section qui est un regroupement de moyen localisé géographiquement et qui
peuvent s’identifier a des départements opérationnels ou fonctionnels. Pour être plus précis la
méthode des sections homogènes structure l’entreprise en sections qui sont en principe des parties
réelle de l’entreprise. Chaque section est un centre de responsabilité. Pour traduire l’activité de la
section, on parlera d’unité d’œuvre, qui va correspondre à la production de la section. La notion
d’unité d’œuvre peut avoir deux interprétations : soit il va s’agir d’une consommation de facteurs
(heure de travail ou quantité de matière 1ère), soit il va s’agir d’un bien semi fini qui va être transférer
à une autre section. En tout hypothèse, les volumes des unités d’œuvre doit être corréler avec la
charge de la section
A la suite du schéma précédent, le cout complet correspond a la somme charge directe, en générale
variable, + charge indirecte provenant des sections. On peut alors en déduire le coût complet du
produit. Le budget global correspond alors a un calcul correspond a la philosophie du direct costing
qui sépare charge variables et charges fixes. On en déduit le budget global pour la période à venir. Si
l’on compare la somme du budget des sections et ce budget global, ils seront différents car, seules
les charges indirectes passent par les sections. Il manque donc au budget de section les charges
directes.
On a coutume d’associer à la méthode des sections homogènes la notion d’imputation rationnelle.
En ce qui concerne la notion d’imputation rationnelle, cela consiste essentiellement dans le fait que
l’on divise la charge de la section en éléments variables et fixes. La partie variable est affectée aux
unités d’œuvre, ce qui nous permet de calculé le cout variable unitaire des unités d’œuvres. Pour ce
qui est de la partie fixe on ne retiendra qu’un % correspondant au taux d’imputation. A partir de là,
on peut calculer un cout de l’unité d’œuvre comprenant des éléments variables et une partie de
charges fixes. Comme toute la charge fixe n’est pas considérée, nous aurons un écart d’imputation,
tantôt négatif, tantôt positif. On fait l’hypothèse quand fin de période ces différences vont se
corriger
La méthode du cout standard
Cette méthode est principalement utilisée dans les activités industrielles où l’on est capable de
mesurer très précisément les consommations de facteurs par produit. Cette définition permet de
faire l’hypothèse que ses consommations par produit correspondent à des charges directes. De fait,
la méthode a été développée pour répondre à trois objectifs :
- Mesurer la consommation par produit en termes de matières premières, main d’œuvre et
machines
- Faciliter la préparation des budgets en termes de charges prévisionnelles
- Etendre la notion de budget au chiffre d’affaire et au profit prévisionnel
On fait ici l’hypothèse qu’un coût standard est une norme de consommation par produit occasionnée
par la réalisation d’un bien (produit ou service). Par extension, on parlera parfois de coût complet
standard qui intègre les frais directs et indirects, des charges variables et fixes. Bien évidemment on
ne va pas se servir du coût complet standard pour préparer le budget.
L’analyse des écarts
Par définition un coût est une charge physique ou financière que l’on va associer à une production. Si
on fait le produit : quantité de facteur x le prix d’achat du facteur, on peut en déduire le volume de
production. L’analyse des écarts a 2 objectifs :
•
confronter pour une période donnée un coût réel à un coût prévisionnel
•
analyser le différentiel qui en résulte pour prendre les décisions adéquates.
Exemple : Soit une entreprise fabriquant des chaussettes à partir de laine
Nb de pelotes
Coût unitaire pelote
Coût total pelotes
Production chaussette
Ecart = prévisionnel – réel
•
coût prévu = 200 F
•
coût réel = 240 F
•
Ecart = 200 – 240 = - 40 Frs
Prévisionnel
100
2
200
300
Réel
80
3
240
250
Quand on constate un écart, les coûts que l’on va comparer peuvent être exprimés en termes
physique ou monétaire. Généralement on dit qu’il existe 3 variables élémentaires qui permettent
d’expliquer les écarts et sur lesquelles on va agir.
•
la différence entre les quantités prévisionnelle et réelle de facteurs de production
•
la différence entre les quantités prévisionnelle et réelle de produits finaux
•
la différence entre les prix prévisionnel et réel des facteurs de production
On peut donner plusieurs explications aux écarts
1) origine p-e dans la gestion des facteurs de production et du capital, quantité de capital
utilisé, corrélativement prix de la main d’œuvre et quantité de la main d’œuvre.
2)
Ensuite on peut se reporter à des causes concernant la variation des volumes de
production réels et prévisionnels
3)
on peut se référer à l’organisation de la production
4) on peut faire intervenir des variables de marché
5) l’écart peut trouver son origine dans un système de standards inadéquate
Calcul des écarts :
•
si l’écart est > 0, l’écart est favorable  (coût réel < coût standard)
•
si l’écart est < 0, l’écart est défavorable  (coût réel > coût standard)
Plus spécifiquement, dans l’analyse des écarts, on parlera de sous écart, qui pourra concerner soit un
sous écart quantité soit un sous écart prix. De façon analogue on décompose les écarts en écarts sur
charges directes et en écarts sur charges indirectes.
En ce qui concerne les écarts sur charges directes, ils répondent à l’équation suivante :
CD = Q * P = α * U
(Quantité facteur * prix achat facteur et aussi quantité de produit fini * α)
La relation précédente permet dans une même équation de visualiser la fonction de production et la
fonction de coût. Dans le cas de la fonction de production, on s’intéresse à la combinaison de facteur
avec le prix d’achat des facteurs. Dans la fonction de coût on s’intéresse au volume fabriqué multiplié
par le coût unitaire.
On a l’habitude de distinguer deux cas de figure :
1) on considère que la quantité de produit réalisé est équivalente à la quantité produite
2) faite que la quantité réalisée est différente de la quantité prévue le coefficient U = coefficient
de produit fini
Quantité produite réalisée = Quantité produite prévue
QS :
quantité standard du facteur de production ou de l’input
QR :
quantité réelle du facteur de production ou de l’input
pS :
prix unitaire standard du facteur de production ou de l’input
pR :
prix unitaire réel du facteur de production ou de l’input
METHODE TRADITIONNELLE
EVALUATION :
ECART GLOBAL = BUDGET MAITRE – BUDGET REALISE
EG = CDS – CDR = QS * pS – QR * pR
ECARTS ET SOUS-ECARTS :
EG = CDS – CDR
= QS *pS– QR *pS + QR *pS – QR *pR
= (QS – QR)* pS + (pS–pR)* QR
= DQ* pS + Dp * QR
= EQ + EP
SOUS-ECARTS :
•
Sous-écart quantité
EQ = (QS – QR) * pS
•
Sous-écart prix
EP = (pS – pR) * QR
Une théorie de la répartition
Quand nous avons examiné les différentes méthodes d’estimation du prix de revient pour chacune
de ces méthodes, nous avons constaté que la difficulté principale résidait dans le problème de la
répartition d’une charge indirecte entre plusieurs départements ou plusieurs produits.
Pour ces différents cas de figure, on a utilisé des règles de répartition qui devaient répondre aux trois
principes suivants :
•
•
•
Principe d’identité
Principe d’unicité
Principe de monotonicité
Toute les règles de répartitions classique répondent à ses trois principes en particulier la règle en
proportion des quantités, la règle en proportion du CA, la règle en proportion d’une charge directe
ou enfin la règle en proportion de la marge/charge directe. On a aussi remarqué que ses règles
aboutissaient à des coûts unitaires identiques par unité du critère.
De fait, quand on utilise la règle en proportion des quantités, les coûts unitaires obtenus sont
identiques. Conclusion, le seul fait de respecter les trois propriétés mentionnées ne nous permet pas
d’assurer que les coûts obtenus par produit correspondent bien à la consommation de ressource. On
en a alors déduit qu’un système de prix de revient pouvait se fixer deux objectifs :
•
•
Soit pour connaître la consommation effective de ressources par produit
Soit pour créer un effet de démonstration
Dans l’analyse que nous allons mener, nous allons nous servir de l’exemple suivant :
Période t
1
2
3
4
Charge
14
15
15
17
Produit 1
5
6
7
8
Production simultanée du produit 1 et du produit 2.
Pour fixer les idées appelons :
-
Ct : charge observée au moment t
t = 1…T
xit : la quantité de bien i réalisée au moment t
i = 1…n
t = 1…T
T>n  plus de période que de produit
Produit 2
4
3
1
1
-
ai : coût unitaire inconnu du bien i
εt ~ N (0 ; Σ²)
A un instant du temps nous avons la relation suivante : Ct = a1 x1t + a2 x2t + … + an xnt + εt
Pour poursuivre notre raisonnement il nous faut expliciter qques hypothèses :
1) les variables de référence Ct et xit sont observées sans erreurs
2) la relation qui lie la charge aux quantités est linéaire ou quasi-linéaire
3) la matrice x des quantités est une matrice non singulière
Sous les 3 hypothèses précédentes et les variables, définir les coûts unitaires ai revient a résoudre
l’optimisation suivante :
Le modèle précédent correspond a un modèle de régression au sens des moindres carré avec une
contrainte linéaire. Du point de vue optimisation il s’agit d’une forme quadratique (type fonction du
second degré) dont nous n’avons pas besoin d’étudier les conditions de second ordre pour nous
assurer qu’elle comporte effectivement un minimum. Le modèle se décompose en 2 parties : une
fonction objective et une contrainte.
Pour préciser le problème, traduisons-le à partir de l’exemple précédent :
min (14-5a1-4a2)² + (15-6a1-3a2)²+ (15-7a1-a2)²+ (17-8a1-a2)²
sc : 26a1+9a2=61
Si l’on observe la forme numérique du modèle, la contrainte (sc) correspond très exactement à la
sommation par colonne. D’un point de vue purement comptable nous avons là la traduction de la
condition d’identité comptable (charges à répartir= charges réparties)
A présent le modèle d’optimisation peut se décrire en substance que l’on a recherché des
coefficients a1 et a2 tels que la somme des erreurs soit minimale. De fait on va minimiser la somme
des εt².
On peut simplifier ça par un lagrangien :
δLδa1= (-5) (14 - 5a1 - 4a2) + (-6) (15 - 6a1 - 3a2) + (-7) (15 - 7a1 - a2) + (-8) (17 - 8a1 - a2) + 26λ = 0
δLδa1= (-4) (14 - 5a1 - 4a2) + (-3) (15 - 6a1 - 3a2) + (-1) (15 - 7a1 - a2) + (-1) (17 - 8a1 - a2) + 9λ = 0
δLδλ= 26a1 + 9a2- 61 = 0
174a1 + 53a2 + 26λ = 401
53a1 + 27a2 + 9λ = 133
26a1 + 9a2 = 61
1745326532792690 x a1a2λ = 40113361
Det = 174 (27x0 – 9x9) - 53 (53x0 – 26x9) + 26 (53x9 – 26x27) = - 7542 ≠ 0
40153261332796190 = a1
a1 = [401 (27x0 – 9x9) – 133 (53x0 – 26x9) + 61 (53x9 – 26x27)] / (-7542)
a1 = 2
1744012653133926610 = a2
a2 = 1
De façon générale la forme quadratique correspond à une famille d’ellipse dont le minimum est
nécessairement 0. Toutefois, en pratique, la contrainte correspondant à l’identité comptable nous
bloque avant d’atteindre cette valeur. On peut, dans les cas pratiques, obtenir des zones telles que le
vecteur de descente n’aboutit pas directement au minimum sous contrainte. Dans la discussion nous
avons insisté sur le point tel que nous devrions avoir une matrice non singulière. La matrice ^x
suivante2448 Det = 2x8 – 4x4 = 0
(1) Ct = Σ ai xit + εt  théorique
(2) Ct = 2x1 + x2  trouvé dans l’exemple
Sous cette forme et en revenant à une conception comptable toute la charge est affectée au produit.
De fait, on peut dire que les coefficients a1 et a2 correspondent à des coûts complets. Pour
retrouver la méthode du coût variable, il faudrait introduire à l’intérieur de l’équation un coefficient
a0, qui correspondrait à une charge non affectée et qui ne serait pas liée au volume de production.
Dans cette dernière conception, la fonction de coût prend la forme suivante :
Ct = i=1naixi+a0+ εt
Ce modèle correspond alors au problème d’optimisation suivant :
minait=1Taixit+a0+εt
Dans cette formulation le coefficient a0 joue le rôle de la contrainte :
min Σ [Ct – a0 - Σai xit] ²
Dans le problème précédant comme il s’agit d’un problème de régression au sens des moindres
carrés on peut estimer la qualité de l’ajustement par le coefficient de corrélation :
R² = 1-Σ ε t²Σ ( Ct- C )²
Dans le cas de l’exemple précédent on obtient un coefficient de corrélation de 1. Cette valeur est
logique car les résidus ε pour chacune des périodes étaient extrêmement faibles. On en conclue
aisément que l’ajustement était bon.
Problème : soit une entreprise réalisant une activité sur 4 périodes avec deux produits réalisés
simultanément.
1) définissez les coûts unitaires complets des produits 1 et 2
2) définissez les coûts variables unitaires des produits 1 et 2 et la charge fixe
3) calculer pour les deux modèles le coefficient de corrélation
Période t
1
2
3
4
Charge
30
35
45
33
Produit 1
3
4
8
9
Produit 2
7
8
9
4
Total
143
24
28
min (30-3a1-7a2)² + (35-4a1-8a2)²+ (45-8a1-9a2)²+ (33-39a1 - 4a2)²
sc : 24a1+28a2=143
170a1 + 161a2 + 24λ = 887
161a1 + 210a2 + 28λ = 1027
24a1 + 28a2 + 0 = 143
170161241612102824280 x a1a2λ = 8871027143
Det = - 37856
a1 = 88716124102721028143280
a1 = 2,1487
a2 = 17088724161102728241430
a2 = 3,2654
Avec un coefficient de corrélation constant (a0)
170161241612102824284 x a1a2a0 = 8871027143
Det = 1260
a1 = 88716124102721028143284
a1 = 1,8667
a2 = 17088724161102728241434
a2 = 2,7905
a0 = 17016188716121010272428143
a0 = 5,0167
En ce qui concerne les fonctions de coût, on remarque rapidement que l’hypothèse de linéarité
suppose des rendements d’échelle constants. De fait, il n’y a pas ici de phénomène d’apprentissage
ou de progrès technologiques tels que des rendements croissants pourraient s’envisager. Pour que
cette hypothèse soit crédible, il faut supposer que nous travaillons sur une modélisation de courte
période (inférieure à 5 ans). Au delà il faut admettre que le progrès technologique va modifier les
comportements et donc les consommations de ressource et par conséquent la structure des coûts.
Cela nous amène aussi à préciser que les charges que nous affectons sont homogènes dans leur
contenu. Par exemple, pour des charges de m-o on va supposer un niveau d’expérience équivalent.
Cette hypothèse est extrêmement importante.
Le graphique précédent permet de remarquer que le positionnement de la nouvelle information
induit un basculement de la droite ou du plan de régression (espace en 3D). Cette situation fâcheuse
peut avoir deux origines :
•
•
soit une erreur dans les relevés de données
soit l’introduction d’une nouvelle technologie qui permet de multiplier la production avec
toujours moins de ressources. On ne peut donc confondre les deux espaces de données
(régression à plusieurs régimes).
La difficulté du problème apparait dès lors que nous avons produit plusieurs biens simultanés.
L’interprétation graphique n’est plus alors évidente.
On peut à présent envisager une situation plus compliqué. Par exemple on peut imaginer le cas où le
nombre de période est inférieure au nombre de produits. Nous sommes alors dans le cas d’un
système sous-déterminé. Il peut y avoir une infinité de solutions au problème.
Exemple : T < n
1
2
Σ
C
11
11
22
1
1
3
4
2
2
4
6
3
3
1
4
4
1
1
2
Dans ce cas de figure les modèles précédents ne permettent plus de trouver une solution adéquate.
Par hypothèse, nous supposons que la relation est tjs linéaire
ai* : coût unitaire inconnu
ai : estimation initiale quelconque du coût unitaire
minai*i=1nai*-ai2
sc. i=1nai*+xit=Ct
pour tout t=1…
Le choix de l’estimation de base ai peut être laissé au décideur ou peut correspondre à la solution
d’une règle classique de répartition. En particulier pour l’exemple précédent, nous pourrions
admettre que les coefficients ai correspondent à une règle en proportion des quantités.
a i-> a1 = a2 = a3= a4 = (22/16) = 1.375
mina1…4=(a1-1.375)2+(a2-1.375)2+(a3-1.375)2+(a4-1.375)2=A
s.c: a1+2a2+3a3+a4=11
s.c:3 a1+4a2+a3+a4=11
δLδa1=a1-1.375+λ+3γ)=0
δLδa2=a2-1.375+2λ)=0
δLδa3=a3-1.375+3λ+γ)=0
δLδa4=a4-1.375+λ+γ)=0
δLδλ=a1+2a2+3a3+a4=11
δLδγ=3a1+4a2+a3+a4=11
100013010024001031000111123100341100
Les carrés noirs sont toujours organisés comme ça lorsque j’ai des équations de ce genre, pour ce
qu’y est des carrés rouges, il s’agit des nombres qui se trouvent dans le tableau….
a1=1.375-λ-3γ=>1.0082
a2=1.375-2λ-4γ=>1.0998
a3=1.375-3λ-γ=>2.1082
a4=1.375-λ-γ=>1.4666
Remplace dans la contrainte :
s.c:(1.375-λ-3γ)+2(1.375-2λ-4γ)+3(1.375-3λ-γ+1.375-λ-γ-11=0
=9-625-11-15λ-15γ=0
=15λ-15γ=-1.375
s.c:31.375-λ-3γ+41.375-2λ-4γ+1.375-3λ-γ+1.375-λ-γ-11=0
12.375-11-15λ-27γ=0
=-15λ-27γ=1.375
15151527 x λγ = -1.375 1.375
Det=15×27-15×15=180
λ=-1.375151.37527=-1.375×27-15×1.375÷180=-0.3208
180
(Même calcule pour γ) =15×-1.375-15×1.375÷180=0.2292
Remplace dans les équations de a1234 retour en haut en vert !!
La modélisation précédente s’identifie au modèle dit quasi optimale. En effet, les solutions que nous
obtenons correspondent à des approximations. De fait nous n’avons aucune certitude que la solution
que nous obtenons correspond exactement au prix unitaire recherché. Ce modèle possède
cependant une propriété intéressante car le nombre de période est identique au nombre de produit,
le modèle optimale donne exactement la même solution que le modèle quasi-optimal (modèle
carré). On remarquera aussi que ce modèle est extrêmement sensible à la solution initiale, en
particulier la modification de l’estimation de départ peut influer sur la solution finale.
Nouveau problème :
c
1
13
2
13
3
25
Σ
51
1
1
2
3
6
2
0
1
2
3
3
3
2
5
10
4
1
0
3
4
5
1
2
1
4
Sur la base d’une estimation initiale dite en proportion des quantités, calculer la solution quasi
optimale pour les 5 produits.
a i-> a1 = a2 = a3= a4 = a5 (51/27) = 1.8889
mina1…5=(a1-1.8889)2+(a2-1.8889)2+(a3-1.8889)2+(a4-1.8889)2+(a5-1.8889)2=A
sc:13= a1+3a3+a4+a5
13= 2a1+a2+2a3+2a5
25= 3a1+2a2+5a3+3a4+a5
1000012301000012001003250001010100001123103110002120200032513000
Puis calculer a12345 et remplace dans sc…..
1
2
3
4
Σ
c
28
30
32
38
128
1
5
6
7
9
27
2
4
3
2
1
10
a1 ; a2 sans coefficient constant (scc) et avec la contrainte (ac)
mina1,2=(28-5a1-4a2)2+(30-6a1-3a2)2+(32-7a1-2a2)2+(38-9a1-a2)2=A
sc:27a1+10a2=128
L=1 2A+λ(27a1+10a2-128)
δLδa1=-528-5a1-4a2-630-6a1-3a2-732-7a1-2a2-938-9a1-a2+27λ=0
191a1+61a2-886 = 0
δLδa2=-428-5a1-4a2-330-6a1-3a2-232-7a1-2a2-138-9a1-a2+10λ=0
δLδλ=27a1+10a2-128=0
191612761391027100×a1a2λ=886304128
Pour l’obtenir de manière plus simple
X=54 637292
XA=C
t
t
X XA =X C
t
-1 t
A = (X X) X C
T
X X = 56794321 x 54637291 = 191616130
T
X C = 56794321 x 28303238
= 886304
C= 28303238
Det (A) = 191 (30x0 – 10x10) + 61 (61x0 – 27x10) + 27 (61x10 – 30x27)
= - 19100 + 16470 – 5400 = - 8030 ≠ 0
88661273043010128100
=a
1
886 (30x0 – 10x10) – 304 (61x0 – 27x10) + 128 (61x10 – 27x30)
= (88600 – 8208 + 103880)/8030
a =4
1
a =2
2
Par principe les modèles quadratiques aboutissent tjs à des systèmes symétriques et carrés. Les
contraintes définissent des vecteurs colonnes et des vecteurs lignes qui viennent s’ajouter au
système de base qui correspondent soit à une matrice identité, soit au produit de la matrice
transposée par la matrice initiale. Suivant ces remarques, le calcul des dérivés n’est pas indispensable
moyennant le recours au calcul matriciel et aux transposés.
Des règles classiques à l’allocation optimale
Dans les discussions précédentes nous avons suggérer une solution telle que le prix de revient
corresponde à un problème d’optimisation. Cela revient à dire que nous avons là un système de
répartition reposant, entre autre, sur l’hypothèse de linéarité. De plus, nous savons que tout
mécanisme de répartition doit répondre à trois propriétés : identité, unicité, monotonicité. Sous les
hypothèses que nous avons admises, le modèle optimal répond à ses trois conditions. Tout le
problème maintenant revient à savoir comment se positionne le modèle optimal par rapport aux
règles classiques. Pour fixer les idées :
minait=1T(Ct-i=1naixit)²
s.c:tCt=tiaixit
ai=aj pour tout i≠j
Propriété 1 : Les règles classiques de la répartition ne sont qu’un cas particulier de la règle optimale
Propriété 2 : L’erreur d’estimation de la règle optimale est tjs plus faible que l’erreur d’estimation des
règles classiques.
Exa :
-
un exo sur les sections homogènes (3 sections principales et une auxiliaire)
un exo sur l’analyse des écarts
un exo avec un peu de tout (allocation optimale, coûts standards, …)
Le modèle précédent permet d’observer que l’introduction d’une contrainte supplémentaire nous
permet de retrouver une règle classique qui est dite en proportion des quantités. Cette observation
permet alors de supposer que toute règle classique pourrait aussi se ramener à un problème
d’optimisation. En fait si l’on considère la contrainte 2, on peut alors imaginer que le modèle
d’optimisation pourrait prendre la forme suivante :
minait=1T(Ct-i=1naixit)²
s.c:tCt=tiaixit
aihi=ajhj pour tout i≠j
aihiquantité=ajhjquantité
Si l’on ne considère que cette dernière formulation, le facteur h présent au dénominateur de la
contrainte correspond strictement à la valeur du critère que l’on se donne. Par exemple, si nous
voulons retrouver la règle en proportion du CA, nous placerons au dénominateur un facteur h
correspond au prix de vente unitaire. Corrélativement, si nous voulons retrouver la règle en
proportion de la charge directe, le facteur h sera alors la charge directe unitaire. Bien évidemment,
tous les critères conduisent nécessairement à une contrainte particulière. De fait, nous avons ici une
formulation très générale où il suffit de connaître le critère de répartition pour pouvoir modéliser
une solution du problème d’optimisation.
Après exercice juin 2009
Une attention particulière doit être apportée dans la combinaison des coûts unitaires et des
quantités physiques : soit on raisonne systématiquement en terme physique, soit systématiquement
en terme monétaire. Ce dernier permettant l’obtention du coût complet. Le budget, lui, correspond
simplement aux quantités prévues que l’on va multiplier par les prix de vente et les prix de revient
que l’on a calculé. Par hypothèse et par principe le prix de revient est défini par la règle de
répartition qui permet l’obtention du meilleur R². Théoriquement, c’est tjs la règle optimale qui
donne le meilleur R² car ses résidus sont tjs les plus faibles. Au niveau de la révision des coûts
standards, on se sert du modèle quasi optimal, ce qui nous permet d’obtenir de nouveaux coûts
unitaires et de procéder dès lors à une analyse des écarts en faisant la différence coûts standards –
coûts réels et en introduisant éventuellement les différentiels de prix d’achats des facteurs (matière
et m-o) et le différentiel de production
Dans la présentation et les modélisations précédentes, nous avons envisagé la relation d’une charge
versus une production de biens et de services.
Dans ce schéma, les charges ne sont pas supposées transiter par des structures intermédiaires telles
des départements ou des sections. A ce schéma simplifié, on pourrait substituer l’idée de structures
dans lesquelles les productions intermédiaires recevraient des charges. On aurait donc un schéma
triangulaire où les charges suivraient le schéma suivant.
Si on étudie ce schéma, en fait nous avons deux systèmes de répartitions : une répartition charges
sur sections, une deuxième répartition section sur produit. Dans la répartition 1 en fait si nous
résonnons dans la philosophie des sections, nous allons calculer les coûts des unités d’œuvres à
partir d’un système d’optimisation pour chaque type de charges. Dans la répartition 2 on répartira
les unités d’œuvres valorisées sur les produits ou services. On peut supposer que les produits ou
services finaux devraient voir leurs coûts soit exprimés en termes physiques, soit exprimés en terme
monétaire, aboutissant ainsi à un concept de coûts complets.
Pour fixer les idées et en ne considérant qu’une charge :
-
Ct (donc le point de départ de mon raisonnement c’est que je considère qu’une seule charge),
ujt (le nombre d’unités d’œuvres réalisées à l’instant t à la section j avec j=1…m et t=1…..T,
T>m)
-
xit la quantité de biens i réalisés à l’instant t.
-
bj le coût unitaire des unités d’œuvres de la section j
-
aji le coût du bien i par rapport à la section j
Nous avons alors deux systèmes de relation :
La 1ère définit le rapport entre la charge et les sections, la seconde relation va définir le rapport entre
la production d’unités d’œuvres et les biens réalisés. Pour chacune des ces relations on peut alors
définir un ensemble de modèles d’optimisation. On peut de façon similaire, écrire un modèle
d’optimisation permettant de calculer les coûts a i pour une section j. On remarquera ici que le
coefficient ai se réfère à des unités d’œuvres u. Le coefficient ai est donc décrit en terme d’unités
d’œuvres (ce n’est pas un prix de revient monétaire c’est un nombre u-o par production).
Bien évidemment comme nous connaissons le coût d’unités d’œuvre b j nous pouvons exprimer
facilement le coût des produits
Problème étoile sur excel:
Ct≅j=1mbjujt ↔section
uit=inSection→produit
(1)
mint=1TCt-j=1mbjujt2
sc=t=1TCt=t=1Tj=1mbjujt
(2)
mint=1Tujt-i=1na
Pour l’exercice quand chercher %quantité et CD
mint=1TCt-j=1muixit2
sc=t=1TCt=t=1Ti=1nmaixit
%q→ ai=aj ∀ i≠j
% CD= aiCDU=ajCDU
Quand on trace le graphique des répartitions, remplacer dans la sc le a 1 puis le a2 pour trouver les
valeurs pour tracer la courbe de condition puis tracer les autres droites en se servant des nombres
trouver lors du calcul des %. (+ Feuille)
Les coûts unitaires par produit et section il faut ajouter que la charge fixe se monte à 40000Fr et que
le prix de l’heure est de 15F et de matière 35F. Préparez les budgets correspondants pour un prix
d’achat de la matière de 39F et de production respectives de 5 et 10 unités.
Le problème précédent peut se décomposer en 2 ensembles de répartitions. Les charges réparties
sur les unités d’œuvres des sections, les unités d’œuvre des sections réparties sur les produis.
Dans le cas d’une modélisation où l’on intègre à la fois les charges, les départements et les produits,
on considère simplement les sections comme productrice d’unité d’œuvre que l’on va « charger »
par l’ensemble des frais occasionnées par leur production. Quand on passe des sections vers les
produits, on va alors répartir les unités d‘œuvres de chacune des sections par produits finaux. On
aura alors le coût d’un produit en termes d’unité d’œuvre de l’une quelconque des sections. Ce coût
de produit peut se transformer en unité monétaire si l’on connait le prix d’achat des facteurs, et à la
limite, en additionnant ces différents coûts de sections en terme monétaire, on peut obtenir un coût
complet.
Ct≅i=1naixit+εt
Un modèle simplifié serait de transférer directement la charge sur les produits (
) correspondant
ainsi à une interprétation classique du modèle de la règle optimale. On peut se poser la question
avec un même jeu de donnée, est ce que les deux traitements induisent les mêmes prix de revient ?
À cette question, la réponse est négative car les estimations des erreurs sont différentes.
Globalement les différences sont minimes mais elles existent.
Corrélativement, on peut s’interroger sur la meilleure estimation possible. En termes d’information,
il n’est pas douteux que les coûts des sections présentent un gros avantage dans une perspective
budgétaire et pour connaitre les coûts de fabrication à chacune des étapes du processus.
Dans une perspective d’une information où la rapidité prime, il ne fait aucun doute que le circuit
simple charges vers produit, est le plus intéressant.
Au delà de cette spécificité, il faut remarquer ici qu’une fois de plus la qualité des résultats repose sur
la qualité des données de base : charge, unité d’œuvre, production.
Si on revient à présent à un cas plus classique qui correspond à un système où nous avons plus de
produits que de période et supposons l’exemple suivant :
C
28
1
5
2
7
3
3
Par hypothèse imaginons que notre coefficient (ai*) correspond simplement à la règle en proportion
des quantités.
ai*  7+5+3 = 15
ai* = 2815  a1*=a2*=a3*=1.87
mina1a2a3(a1-1.86)2+(a2-1.86)2+(a3-1.86)2
sc:5a1+7a2+3a3=28
On peut trouver la matrice tout de suite :
1005 0107 0013 5730 x a1a2a3λ = 1.861.861.8628
Solution a1 ; a2 ; a3 = 1,86 (obtenu par la matrice), alors que la vrai solution c’est a1 = 3 ; a2 = 1 ; a3 = 2
Dans le cas du modèle quasi optimal avec une seule période d’information et si l’on choisi une règle
pour une approximation initiale correspondant au prorata quantité, la solution du modèle nous
ramène à ce même prorata et ne nous permet d’obtenir les véritables coûts unitaires.
Cette particularité extrêmement fâcheuse nous rappelle que le modèle quasi optimal ne nous donne
qu’une approximation et que dans le cas mono période, l’approximation correspond exactement à la
répartition initiale.
De fait, le modèle est extrêmement influencé par la solution initiale.
Supposons à présent que nous disposons du jeu de données suivant :
C
28
34
1
5
4
2
7
6
3
3
8
Sur la base de cet information et en se servant tjs de la règle en proportion des quantités, estimons la
solution quasi optimal.
a1*=a2*=a3*=1.87
min=(a1-1.87)2+(a2-1.87)2+(a3-1.87)2
sc=5a1+7a2+3a3=28
sc=4a1+6a2+8a3=34
1005401076001385730046800 x a1a2a3λ1λ2 =
1.871.871.872834
On trouve alors les solutions suivantes : a1 = 1.85 ; a2 = 1.846 ; a3 = 1.44.
Ce n’est pas tout à fait la même solution car une 2ème ligne (contrainte supplémentaire) apparaît : ça
apporte de l’information.
On remarquera dans ce dernier exemple que les solutions du modèle ne correspondent plus à
l’estimation initiale en proportion des quantités. Cela découle du fait que l’on a rajouté de
l’information sous la forme d’une ligne supplémentaire. C’est cette nouvelle période qui fait varier
l’estimation. Toutefois, nous n’obtenons tjs pas la vraie solution. Le modèle n’est donc pas parfait. Il
demeure tjs très sensible à l’estimation initiale.
Dans l’hypothèse on l’on dispose tjs de peu d’information, on pourrait alors introduire des
contraintes sur la base d’une information subjective tel que nous ayons une contrainte classique
mais où l’on admettrait que certains coûts unitaires sont supérieurs ou inférieurs à certains autres.
minaii=1n(ai-ai*)2
sc=i=1naixit=Ct∀t=1….t*
ai≥aj ∀ i≠j
Evidemment la création de ces contraintes demande une information supplémentaire sur les
rapports pouvant exister entre les coûts unitaires (ai et aj).
Si cette information n’est pas pertinente, on pourrait se retrouver dans le cas classique de règles
arbitraires.
En ce qui concerne ce modèle, sa résolution est assez délicate car en plus des contraintes classiques
d’égalité, nous rajoutons des conditions d’inégalité qui sont difficiles à résoudre.
Exercice sur la répartition Excel (Analyse des écarts)
min=(a1-1.1142)2+(a2-1.0114)2
sc=7a1+3a2=12
min=(a1-2.1142)2+(a2-2.0114)2
sc=7a1+3a2=25
107013730 x a1a2λ = 1.11421.011412
107013730 x a1a2λ = 2.11422.011425
Standard
Réel
Ecart
1.1142
1.2548
- 0.14
1.0114
1.0722
- 0.6
MO
MA
2.1142
2.6168
- 0.5
2.0114
2.2274
- 0.21
Nature des écarts
Défavorable
Défavorable
Défavorable
Défavorable
Dans le calcul des écarts, dans la forme présente avec des productions et des réalisations identiques
et sans connaissance du prix d’achat des facteurs, l’écart prix et l’écart quantité se résume à la
différence entre les coûts unitaires standards et les coûts unitaires réels.
Le problème pourrait être différent si par exemple, les quantités prévues devenaient différentes des
quantités réelles. A ce moment la on pourrait faire une interprétation en termes d’écart de volume
lié à la variation de la production.