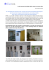20 π + 4

1ère S
DEVOIR MAISON N°2
à rendre le jeudi 16 octobre 2014
Travail par groupes de 2, 3 ou 4.
1) Partie informatique
a) Sur Géogebra, construire les points A(0,0) et B(10,0).
Créer un curseur X puis placer le point M de coordonnées
(X,0). Construire alors les points C, D, E et F de façon à
obtenir la figure ci-contre. (Attention : quand on fait varier X,
la point M doit se déplacer sur le segment [AB] et les points
C, D, E et F doivent eux aussi se déplacer de façon à ce que
la figure comporte toujours deux carrés comme ci-contre)
b) En faisant varier X conjecturer la valeur de X pour laquelle
la somme des aires des deux carrés est minimale.
c) Faire une figure analogue avec un point M variable sur
[AB] en s’intéressant cette fois, à la somme des aires de deux disques de diamètres respectifs [AM] et [MB] .
Pour quelle position de M cette aire est-elle minimale ?
d) Faire une nouvelle figure, avec M variable sur [AB], un carré de côté AM et un disque de diamètre [MB].
Conjecturer la position du point M pour que la somme de ces deux aires soit minimale.
2) Partie mathématique
a) On reprend la première situation (avec les deux carrés). On pose x = AM.
 Exprimer l'aire des carrés AMCD et MBEF en fonction de x.
 Prouver que la somme des aires des deux carrés s'exprime par la fonction f définie par
f (x)  2x 2  20x  100 .

En déduire la position du point M pour que la somme des aires des deux carrés soit minimale.
b) On reprend la deuxième situation (deux disques). Exprimer en fonction de x la somme des deux aires et
déterminer pour quelle valeur de x cette somme est minimale.
c) ) On considère maintenant la troisième situation (un carré et un disque).
Démontrer que la somme des aires du carré et du disque est minimale lorsque le rayon du disque est égal à
20
.
 4
Travail à rendre (pour chaque groupe) :


les fichiers geogebra envoyés par mail par le biais de la messagerie de l’ENT Lea
[email protected] pour les 1ère Sa
[email protected] pour les 1ère Sb
les conjectures et la partie mathématique soigneusement rédigés sur une copie double.
a) x = AM.
AMCD a donc pour aire x²
MB = AB – x = 10 – x et MBEF a pour aire (10 – x)²
La somme des aires de ces deux carrés est donc :
f ( x)  x²  (10  x)²  x²  100  20x  x²  2x²  20x  100
Comme f est une fonction polynôme du second degré, on
peut étudier ses variations.
L’extremum est un minimum (car le coefficient de x² est
b 20
positif) et il est atteint en

5.
2a 4
La somme des aires est minimale quand x = 5 donc quand M
est le milieu de [AB]
b) On a toujours AM = x et BM = 10 – x.
La somme des aires est :
 x
 10  x 
g ( x)       

2
 2 
x ²  100  20 x  x ²

4
2
2

x ²  5 x  25
2
On obtient une fonction polynôme du second degré,
qui a un minimum (car le coefficient de x² est positif).

Ce minimum est atteint en
b
5

5
2a 2  
2
Dans ce cas aussi, la somme des aires est minimale quand x = 5 donc quand M est le milieu de [AB]
c) Cette fois, la somme des aires est :
 10  x 
h( x )  x ²   

 2 
100  20 x  x ²
 x²  
4
4 x ²  100  20 x   x ²

4
4

 5 x  25
4
Cette fonction polynôme du second degré admet un minimum en
b
5
5
2
10


 5 

4


4


2a 2 
4   4
4
2
10
10 
10
10  x
  4  10  40  10  1  40  20 CQFD !

Quand x 
le rayon du disque est :
 4
2
2
 4
2 2(  4)   4
2