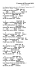La diagonale de Cantor

Le drame subjectif de Cantor - Conférence du 17 mars 2007
La diagonale de Cantor
Merci Virginia pour cette introduction,
Merci à vous d’être là.
Virginia et Henri m’ont proposé d’intervenir dans le cadre de notre cycle de
conférences pour parler de la diagonale de Cantor.
J’espère que mon exposé sera à la hauteur de leurs attentes.
Dans l’argument proposé sur le site j’ai essayé de restituer quelque chose de la
fraîcheur des questions concernant l’infini telles qu’elles se présentaient avant Cantor.
Dans l’introduction je rappellerai, un peu comme tu viens de le faire Virginia, les
enjeux de notre séminaire, en quoi "le drame subjectif de Cantor", mais plus
généralement le "drame du savant" nous concerne.
Par avance pardon pour la longueur de cette introduction mais elle me semble
nécessaire.
Ensuite nous ferons, rapidement bien sûr, un état des lieux : l’infini avant Cantor.
Puis nous rentrerons dans le vif du sujet avec les ensembles équipotents, la remise en
cause du neuvième axiome d’Euclide et l’émergence, grâce à l’argument diagonal, de
deux types d’infinis radicalement hétérogènes :
La puissance du dénombrable et la puissance du continu
Si nous en avons le temps, je dirai deux mots du théorème de Cantor et de la théorie
des transfinis.
Enfin, ensemble et à partir de ce que vous aurez à en dire, nous conclurons.
Difficile de parler du concept d’infini, dans le champ des mathématiques, sans lui associer
ceux de limite et de continuité.
La première approche de ces notions se trouve accrochée, cristallisée par les paradoxes
de Zénon d’Elée ( 490-450 av J.C.) et en particulier par celui bien connu d’Achille et la
tortue*.
*Achille et la tortue est l’argument de Zénon pour prouver l’impossibilité d’écrire le mouvement. Il démontre, par un discours, qu’Achille ne
rattrapera jamais la tortue partie avant lui.
Supposons que la tortue ait pour simplifier un mètre d’avance et qu’Achille court deux fois plus vite qu’elle. Lorsque qu’Achille aura
parcouru le mètre de retard qu’il a sur la tortue celle-ci aura parcouru un demi-mètre et ainsi de suite à l’infini.
A____1____T
………….. A__½__T
…………………….A_¼_T
………………………….………etc. à l’infini
L’idée c’est qu’il doit d’abord passer par le point où était la tortue au moment de sont départ, et que ce processus se reconduit à l’infini.
Alors bien sûr nous pourrions nous dire que ce paradoxe est installé par le langage : il a fabriqué un discours qui conduit à une contradiction
car si nous faisons courir Achille, il va la rattraper la tortue, il n’y a aucun problème là dessus.
Pourtant il réussit à créer par son discours un impossible.
1
Ces paradoxes s’inscrivent dans une dialectique, celle qui réfute la réalité du
mouvement. Plus exactement la possibilité logique d’écrire le mouvement.
A l’époque de Zénon deux conceptions (déjà) s’opposaient : celle des continuistes qui
pensaient le nombre, l’espace, le temps et la matière comme divisible à l’infini et la
conception atomiste qui préconisait l’existence d’éléments premiers indivisibles.
Ces paradoxes, qui défiaient les lois de la logique, eurent pour conséquence une
grande méfiance de la part des mathématiciens à l’égard du concept d’infini.
Désormais il sera distingué :
- l’infini potentiel qui restera en usage chez les mathématiciens et
- L’infini en acte qui lui sera rejeté par Aristote pour qui il était exclu de
manipuler l’infini comme un objet, dans la mesure ou pour l’époque infinité et
imperfection (dans le sens générateur de paradoxes) se trouvaient
irrémédiablement liées.
A partir du moyen âge apparaît une conception théologique d’un infini en acte, pris
cette fois si d’un point de vue qualitatif, celui d’un Dieu parfait et omnipotent.
J.P. Hiltenbrand nous rappelait récemment que les arguments de Nicolas de Cuse témoignent
assez bien de son époque :
…J’appelle maximum une chose telle qu’il ne puisse pas y en avoir de plus grande. –
tout simplement – Il est absolu, il est en acte, tout l’être possible, ne subit des choses
aucune restriction et en impose à toutes.
Ce maximum, que la foi indubitable de toutes les Nations révère comme Dieu sera,
dans mon livre, premier sur la raison humaine l’objet que, sans jamais pouvoir le
comprendre, je m’efforcerai de rechercher sous la conduite de Celui qui seul habite
dans une lumière inaccessible…
…Il s’agit donc d’un maximum tel qu’il ne puisse y en avoir de plus grand, il est
absolu et il est impossible à comprendre et donc : Docte ignorance. Maximum et
minimum, je le dis tout de suite, coïncident dans leur valeur et est au-dessus de toute
opposition pensable et possible. Le maximum est un et il représente la nécessité
absolue…
…Ignorance de l’infini parce que nous sommes dans l’incapacité de le connaître…
Pour Nicolas de Cuse l’infini n’est pas du domaine du savoir, de la connaissance mais
de la Docte ignorance qui témoigne de nos limites.
Nous attendons avec beaucoup d’intérêts la conférence de Marie-Charlotte Cadeau
sur :
L’infini, négation des déterminations : chaos ou néant ?
à la fin du mois qui abordera en détail ces questions.
Les arguments d’Aristote régneront en maître durant plusieurs siècles et il est à noter
qu’aujourd’hui encore certains mathématiciens s’opposent à penser l’infini comme
2
défini. Pour eux l’infini est un concept qui désigne quelque chose « en puissance »
mais jamais réalisé et qui remettent en cause l’infini en acte.
Depuis Cantor, mais déjà avant lui Bolzano et quelques autres, une majorité de
mathématiciens tiennent l’infini pour un concept entier et défini mais il est intéressant
de constater que les travaux et le dire de Cantor n’ont pas entièrement absorbé les
questions sur l’infini, infini qui d’une certaine manière a toujours fait bord :
-
En acte, dans le champ métaphysique comme limite du pensable
En puissance, dans celui du calcul comme borne inaccessible
Une des questions que soulève cette vieille et tenace querelle est de savoir si les
scientifiques disposent de quelque preuve de cet infini-défini. Car si la réponse était
positive cela donnerait une justification physique au concept.
Nous pouvons par exemple considérer les trous noirs, état limite de l’évolution d’une
étoile, comme des infinis actuels.
Je vais vous lire un extrait de l’entretien avec Jean-Pierre Luminet, l’un des auteurs
avec Marc Lachièze-Rey (tous les deux du CNRS), du livre : De l’infini… Mystères et
limites de l’Univers (Dunod, 2005)
A la question :
Mais l’infini actuel n’existerait-il qu’en mathématiques ?
J.P. Luminet répond :
Une première remarque s’impose. Distinguer comme nous le faisons un infini
mathématique et un infini dans la nature pose un problème fondamental : les
mathématiques, n’est-ce pas aussi la nature ? Cette contradiction n’est toujours pas
résolue.
Seconde remarque : il faut noter qu’au sein même des mathématiques, le statut actuel
ou potentiel de l’infini n’est pas clair. Certaines écoles réfléchissent d’ailleurs sur la
philosophie des mathématiques, sur le sens profond de cette démarche : est-ce une
sorte de langage universel ou une création de l’esprit humain ? On pourrait croire
qu’avec les travaux fondamentaux de Cantor ou de Gödel, par exemple, l’infini actuel
en mathématiques est accepté par tous, mais il n’en est rien. Il y a encore des écoles –
rappelons-nous les Intuitionnistes au début du XXe siècle – qui dénient toute actualité
à l’infini. La très grande majorité des physiciens conteste aussi toute réalité à l’infini
actuel.
Il n’existerait qu’en mathématiques.
Toutefois, une branche particulière de la physique qui est la cosmologie et dans
laquelle les deux auteurs de cet ouvrage travaillent, lui accorde une existence.
Cette question, concernant la preuve de cet infini-défini, rejoint celle régulièrement
soulevée par Lacan, concernant le Réel : est-il à inventer ou à découvrir, et la question
n’est en rien anecdotique.
3
Leçon du 17/01/62, séminaire sur l’Identification :
…Pour que le Dieu de Descartes existe, il faudrait que nous ayons un petit
commencement de preuve de sa volonté créatrice à lui dans le domaine des
mathématiques.
Or ce n’est pas lui qui a inventé le transfini de Cantor, c’est nous.
C’est bien pourquoi l’histoire nous témoigne que les grands mathématiciens qui ont
ouvert cet au-delà de la logique divine, Euler tout le premier, ont eu très peur. Ils
savaient ce qu’ils faisaient ; ils rencontraient, non pas le vide de l’étendue du pas
cartésien qui finalement, malgré Pascal, ne fait plus peur à personne, parce qu’on
s’encourage à aller l’habiter de plus en plus loin, mais le vide de l’Autre, lieu
infiniment plus redoutable, puisqu’il y faut quelqu’un.
Le deuxième extrait choisi se trouve dans les Autres écrits. Le texte date de décembre 67 et a
pour titre :
La méprise du sujet supposé savoir.
…Si la découverte du nombre transfini, nous pouvons fort bien la supposer s’être
ouverte de ce que Cantor ait achoppé à tripoter diagonalement les décimales, nous
n’irons pas pour autant à réduire la question de la fureur que sa construction
déchaîne chez un Kronecker ? Mais que cette question ne nous manque pas cette autre
concernant le savoir ainsi surgi : où peut-on dire que le nombre transfini comme
« rien que savoir », attendait celui qui devait se faire son trouveur ?
Si ce n’est en aucun sujet, c’est en quel on de l’être ?
Le sujet supposé savoir, Dieu lui-même pour l’appeler par le nom que lui donne
Pascal, non pas le Dieu d’Abraham, d’Isaac et de Jacob, mais le dieu des
philosophes, le voici débusqué de sa latence dans toute théorie.
Toujours dans le même texte mais un peu plus loin :
…Cette place de Dieu-le-père, c’est celle que j’ai désignée comme le Nom-du-Père**
et que je me proposais d’illustrer dans ce qui devait être ma treizième année de
séminaire (la onzième à Sainte-Anne) quand un passage à l’acte de mes collègues
psychanalystes m’a forcé d’y mettre un terme, après sa première leçon.
Je ne reprendrai jamais ce thème, y voyant le signe que ce sceau ne saurait être
encore levé pour la psychanalyse.
Il y a là, dans ce texte, une dimension presque dramatique : la référence régulière de
Lacan à Cantor n’est pas seulement par rapport à sa théorie et à ses mathèmes mais
aussi dans un point d’identification au drame du savant qui avance et se heurte aux
résistances de ses pairs comme du champ social car toute invention, chaque savoir
nouveau implique une remise en cause de l’ordre établi.
** Pour les non-Lacaniens présents dans la salle :
Concept forgé par J.Lacan, à partir de 53 pour désigner la métaphore paternelle, sous la forme d’un signifiant, le Nom-du-Père. Opération
symbolique qui valide, dans l’après coup de la substitution signifiante, celle de la castration qui limite et ordonne le désir du sujet.
Elle s’inscrit (cette métaphore) dans une refonte et une réécriture du complexe d’Œdipe par l’intermédiaire des registres du Réel, de
l’Imaginaire et du Symbolique.
Le Nom-du-Père dans le champ de la théorie permet depuis Lacan d’écrire ( et seulement d’écrire car cela ne dévoile rien de son mystère) ce
qui fait défaut chez le psychotique à savoir la forclusion du Nom-du-Père, c’est à dire l’échec de la métaphore paternelle qui prive le sujet de
l’instance Symbolique du père et le maintient dans une jouissance " hors-bord ", non vectorisé par le désir.
4
Le Nom-du-Père était en effet le titre que Lacan destinait à son séminaire de l’année
63-64.
Seule la première leçon fut prononcée.
Le séminaire de Lacan fut interrompu jusqu’en janvier et il repris, non pas à SainteAnne où il avait lieu depuis plusieurs années, mais rue d’Ulm grâce à Althusser avec
pour titre : Les quatre concepts fondamentaux de la psychanalyse.
Par la suite J. Lacan désigna toujours son Séminaire non prononcé sous le titre :
Les noms du père et en 73 son Séminaire avait pour titre : les non-dupes errent.
Enfin pour clore cette longue introduction, je m’en excuse encore, un passage du Séminaire
de 73-74, leçon du 19 février :
…Ce qu’il faut que vous sachiez comme pas supplémentaire, c’est de vous apercevoir
que si ce que je vous rends sensible en vous disant que l’inconscient ça ne découvre
rien, puisqu’il n’y a rien à découvrir, il n’y a rien à découvrir dans le Réel, puisque là
il y a un trou, si l’inconscient là invente, c’est d’autant plus précieux de vous
apercevoir que dans la logique c’est la même chose, à savoir que si Aristote ne l’avait
pas inventé, son premier frayage, à savoir fait passer du dire dans ce concassage de
l’être grâce à quoi il fait des syllogismes- bien sûr on avait fait du syllogisme avant
lui, simplement on ne savait pas que c’étaient des syllogismes. Pour s’en apercevoir,
il faut l’inventer ; pour voir où est le trou, il faut voir le bord du Réel.
Le 9 avril, il reprend cette question du savoir, du trou du Réel et de son bord, par ce lumineux
raccourci :
l’invention, c’est l’écrit et la fonction de l’écrit c’est de faire bord.
Et cette invention se trame à partir d’un savoir inconscient, raison pour laquelle la
théorie de Cantor nous concerne, bien au-delà de son histoire personnelle.
Le problème n’est pas de rechercher ou d’établir quelque chose qui serait de l’ordre de
la vérité du sujet Cantor.
Cantor est mort, lui seul aurait pu éventuellement mettre du sens à ce qui lui est arrivé.
Ce qui nous intéresse aujourd’hui c’est d’interroger son œuvre et ses mathèmes pour
tenter d’en articuler le savoir nouveau surgit à l’occasion du déplacement, par
l’écriture, du Réel, de l’impossible qu’avait constitué jusqu’à lui l’infini dans le champ
des mathématiques, mais aussi bien dans celui de la pensée.
L’infini mathématique avant Cantor
Comme je l’ai rappelé à l’instant les Grecs avaient contourné le problème de l’infini
pour ne pas mettre en péril leur système de pensée logique.
Cependant, certaines questions furent débattues au fil des siècles pour modifier ou
nuancer la conception d’Aristote :
Y-a-t-il un seul infini ou plusieurs ?
S’il y en a plusieurs, comment les comparer ?
Peut-on augmenter un infini ?
5
Ces questions, dans leur tentative de réponse, se heurtaient à des paradoxes, en
particulier comme nous allons le voir à travers quelques exemples, l’infini
contrevenait à l’un des axiomes fondamentaux de la géométrie euclidienne.
Au XVIIème siècle
Pour Pascal les nombres n’avaient nuls besoins d’être définis et se rattachaient
directement à la mesure des grandeurs, et cela est resté vrai jusqu’à Cauchy (début du
XIXème). Et dans le monde des grandeurs nul besoin d’un infini en acte, il suffit de
supposer cette grandeur potentiellement aussi grande que l’on veut.
Le calcul infinitésimal, inventé simultanément par Isaac Newton et Wilhelm Gottfried
Leibniz substitue au couple fini/infini le couple défini/indéfini et introduit des quantités
infiniment petites.
Un certain nombre de règles vont permettre de "calculer" avec l’infini.
Par exemple :
On ne change pas l’ordre d’un infiniment grand en lui ajoutant une quantité
finie.
Mais l’infiniment grand n’est toujours pas un infini défini.
D’autre part, se met en place une hiérarchie opératoire fondée sur la croissance
comparée des fonctions lorsque la variable tend vers l’infini mais ces quantités
infiniment petites ou infiniment grandes n’ont pas de consistances en soi.
Ces règles vont permettre de donner une réponse à certaines des questions soulevées
par l’infini mais sans surmonter pour autant les vrais difficultés.
Celle par exemple soulevée par le paradoxe de Galilée :
(rappelons que pour lui le "livre" de la nature était écrit en langage mathématique).
1
1= 1²
2
3
2
4=2²
5
6
7
8
3
9=3²
…etc. à l’infini
En comparant la collection des entiers avec celle de leurs carrés il avait constaté que
chaque entier a un carré et que réciproquement chaque carré est le produit d’un entier
multiplié par lui-même, ce qui contrevenait au neuvième axiome de la géométrie
euclidienne ***:
Le tout est plus grand que la partie
Intuitivement, nous avons le sentiment qu’il y a plus de nombres entiers que de carrés
parfaits.
Leibniz manipule et donne un statut à l’infini qui légitime son maniement sans pour
autant admettre l’infini en acte.
***Dans ses éléments, Euclide a en effet défini les fondements de sa géométrie sous la forme de neuf axiomes et cinq postulats.
6
Pas question non plus pour lui de remettre en cause le neuvième axiome de la
géométrie euclidienne, il rejettera le paradoxe de Galilée qui ne se soutient qu’a
condition de considérer ces collections comme des entités achevées.
► Point fondamental qui divise, comme le rappelait Virginia tout à l’heure, aujourd’hui
encore Cantoriens et non-cantoriens : pour comparer deux collections, il est nécessaire de les
supposer actuelles, réalisées.
Ce n’est qu’à la seconde moitié du XIXème siècle que s’est vraiment construit l’édifice
des nombres, des nombres réels.
Pourquoi ?
Par souci de rigueur dans les démonstrations, c’est à dire ne plus se baser sur des
concepts "évidents" de la géométrie.
Le nombre n’est plus identifié à une grandeur.
Par exemple au milieu du XIXème siècle les notions fondamentales de continuité, de
convergence d’une série ne sont pas clairement définies.
C’est Bernard Bolzano ( 1781-1848) qui donna le premier une définition correcte de la
convergence d’une série.
C’est lui également qui fit le pas d’envisager dans le champ mathématique l’infini
actuel, mais il resta englué dans les paradoxes de l’infini ne s’autorisant pas à remettre
en cause le fameux axiome :
Le tout est plus grand que la partie
"Les paradoxes de l’infini" était justement le titre de son livre. Il parut en 1851 et passa
presque inaperçu.
Vingt ans plus tard Cantor prit semble-t-il connaissance de cet ouvrage grâce à un
article qui le signalait favorablement.
…………………………………………………………………………………………………..
La suite de la conférence s’est déroulée au tableau !
Points abordés.
• Rappels de quelques éléments de la théorie des ensembles, pré requis pour la suite.
N = {ensemble des entiers naturels}
0 ,1 ,2 ,3 ,4 , 5, 6,……….etc. à l’infini
Z = {ensemble des entiers relatifs}
………….(-6), (-5), (-4), (-3), (-2), (-1), 0 ,1 ,2 ,3 ,4 ,5 , 6 ……………….
L’ensemble N est un sous-ensemble de Z
Q = {ensemble des nombres de rationnels, de la forme : q = n/d avec n ΥZ et d ΥZ*}
…( -1) ,… , (-1/2) ,…, (-1/3) ,…, (-1/4) ,…, (-1/5) ,…,0,…,1/5 ,…, 1/4 ,…,1/3 ,…,1/2 ,…,1,…, 3/2 ,…
L’ensemble Z est un sous-ensemble de Q
R = {ensemble des nombres réels : les rationnels plus les irrationnels}
L’ensemble Q est un sous-ensemble de R
7
N = Z = Q= R
Depuis Cantor, nous identifions l’ensemble R à l’ensemble des points d’une droite infinie :
-∞
-1
-1/2
0
1
1/2
+∞
√2
•
L’ensemble des parties d’un ensemble
L’un des axiomes de la théorie des ensemble dit que, pour tout ensemble E , il
existe un ensemble, noté P(E), tel que:
A Υ P(E) si et seulement si A = E
Exemple :
Soit E un ensemble à trois éléments : E = { a, b, c }
Nous allons construire toutes les parties, tous les sous ensembles de E :
a
Pour
chacun
des
éléments
de
E
nous
décidons
de
le
choisir
ou
pas
pour
construire
tous
les
sous-ensembles
possibles
b
c
L’ensemble des
parties de E
Oui
{a, b, c}
Non
{a, b}
Oui
{a, c}
Non
{a }
Oui
{b, c}
Non
{b}
Oui
{c}
non
{ }= φ
l’ensemble vide
Oui
Oui
Non
Oui
Non
Non
P(E) = { {a, b, c} , {a, b} , {a, c} , {a } , {b, c} , {b} , {c} , { } }
Nombre d’éléments de (P(E) )= 8 = 2³
8
•
Ensembles équipotents :
« Un ensemble E est équipotent à un ensemble F s’il existe une bijection de E sur F :
à tout élément de E correspond un et un seul élément de F »
exemple :
E = { a , b , c } et F = { Ο ,  , ∇ }
a↔Ο
b↔
c↔∇
► L’équipotence est "l’outil" qui va nous permettre de comparer les ensembles infinis.
Deux segments PQ et P’Q’ de longueur différente ont le même nombre d’éléments.
En effet, nous pouvons faire correspondre à chaque point M du premier segment un et
un seul point M’ du second segment, et réciproquement.
Plus surprenant encore : l’ensemble des points contenus dans un carré a le même
nombre d’éléments que celui des points du coté de ce même carré.
( nous conseillons au lecteur, pour toutes ces questions, la lecture du Hors Série de la
Recherche sur l’univers des Nombres - août 1999)
Cantor utilisera le terme de puissance pour désigner ce qu’il nommera par la suite
cardinal d’un ensemble, soit le nombre d’éléments de l’ensemble.
A propos du terme de puissance, il dira :
…J’ai emprunté l’expression puissance à Jacob Steiner qui l’utilisa dans un sens tout
à fait spécial, quoique très proche, pour dire que deux figures géométriques sont tirées
l’une de l’autre par coordination projective. C’est à dire qu’à chaque élément de l’une
correspond un et un seul élément de l’autre.
(Réf.: Infini et Inconscient-Essai sur Cantor de Nathalie Charraud – Edit. Anthropos)
Quelques résultats :
- Concernant la puissance de l’ensemble des parties d’un ensemble E :
( voir plus haut la démonstration du résultat pour n =3 )
Si la puissance de (E) = n alors la puissance de (P(E)) = 2ⁿ
- Si intuitivement, nous trouvons raisonnable que :
La puissance de l’ensemble des nombres pairs = La puissance de l’ensemble des nombres impairs
- Il nous semble plus étonnant de constater que :
9
La puissance de (N ) = La puissance de (Z ) = La puissance de (Q)
( nous conseillons au lecteur, pour toutes ces questions, la lecture du Dominos consacré à
l’infini en Mathématiques de Norbert Verdier chez Flammarion)
Une question alors se pose :
L’ensemble des nombres réels R a-t-il lui aussi la même puissance que N ? .
Autrement dit :
Est-il possible de "compter" les nombres réels ?
•
L’argument diagonal – la puissance du dénombrable et la puissance du continu
Pour répondre à la question, et devant la difficulté de la tâche ( essayez vous
verrez), l’idée est de raisonner par l’absurde.
Supposons qu’il soit possible de "compter" les nombres réels.
Nous allons travailler avec une partie de R : numérotons les réels compris entre
0 et 1.
X1
X2
X3
X4
X5
X6
X7
.
.
.
etc
=
=
=
=
=
=
=
0,
0,
0,
0,
0,
0,
0,
3
5
1
1
2
0
9
6
1
2
0
8
0
9
9
2
4
1
6
0
9
2
6
2
1
9
3
8
1
4
1
1
7
5
2
8
9
1
1
4
8
5
1
2
5
1
1
1
6
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Nous allons construire un nombre réel Y compris entre 0 et 1 et pourtant
différent des Xn, quelque soit la valeur de l’entier n, ce qui contredira notre
hypothèse de départ.
Règle choisie pour la construction de Y :
la i ème décimale de Y sera égale à 1 si la i ème décimale de Xi est différente de 1
et 0 si non.
10
Construction de Y:
Si i = 1 :
X1 = 0,
3
6
9 2 1 8 1
.
.
.
La première décimale de X1 est différente de 1 donc :
Y = 0, 1………
Si i = 2 :
X2 = 0,
5
1
2 6 4 9 2
.
.
.
La deuxième décimale de X2 est égale à 1 donc :
Y = 0,
1 0………
Si i = 3 :
X3 = 0,
1
2
4 2 1 1 5
.
.
.
La troisième décimale de X3 est différente de 1 donc :
Y = 0,
1
0 1……
Et ainsi de suite jusqu’à l’infini.
Finalement Y est égal à :
Y
= 0,
1
0
1 0 1 1 1
.
.
.
Y est différent, par construction, de chaque Xn, ce qui contredit notre hypothèse
de départ :
X1
X2
X3
X4
X5
X6
X7
.
.
.
etc
=
=
=
=
=
=
=
0,
0,
0,
0,
0,
0,
0,
3
5
1
1
2
0
9
6
1
2
0
8
0
9
9
2
4
1
6
0
9
2
6
2
1
9
3
8
1
4
1
1
7
5
2
8
9
1
1
4
8
5
1
2
5
1
1
1
6
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Conclusion :
L’ensemble R des nombres réels a une puissance supérieur à celle de N.
La puissance de (N ) = La puissance du dénombrable
≠ La puissance de (R) = La puissance du continu
11
•
Les transfinis
cardinaux
ordinaux
Les nombres entiers finis
Card.( φ ) =
0
Card ({φ}) = Card
({0}) = 1
0
0 a un statut particulier dans la théorie des nombres. Il fait
l’objet d’un axiome.
Il n’a pas d’antécédent.
1
1 est le successeur de 0 : 1 = 0+1
Card
({φ, {φ}) = Card ({0, 1}) = 2
2
2 est le successeur de 1 : 2 = 1+1
Card
({φ, {φ}, {φ, {φ}}) = Card ({0, 1, 2}) = 3
3
3 est le successeur de 2 : 3 = 2+1
.
.
.
.
n+1
.
.
.
Card
({0, 1, 2, 3, 4, 5,…, n}) = n+1.
.
.
successeur de n.
Les nombres transfinis
card.
({0, 1, 2, 3, 4, 5,...}) = card.( N ) = ‫א‬0
‫א‬0 = ω
‫א‬1
La
question
qui tourmentera
Cantor :
où placer la
puissance
du continu
dans
la hiérarchie
des
cardinaux ?
‫א‬2
‫א‬3
.
.
.
Puis. du dénombrable= plus petit des ordinaux transfinis
ω+1
ω+2
ω+3
……
……
2ω
2ω + 1
2ω + 2
……
……
ω²
ω² + 1
……
……
12
•
Théorème de Cantor
Pour tout ensemble A :
Card.( A) < Card.( P(A))
En particulier :
Puissance du dénombrable
•
‫א‬0 <
Puissance du continu
L’ Hypothèse du continu :
Il n’existe pas d’ensemble dont le cardinal soit strictement supérieur à card. (N) et
strictement inférieur à card. (P(N))
= ‫א‬1
Jean Dieudonné ( l’un des fondateurs de Bourbaki) dans son article Mathématiques
vides et mathématiques significatives (Penser les mathématiques – Seuil) dit ceci à
propos de l’hypothèse du continu :
… Ce qui nous intéresse beaucoup, en tant que garde- fou, ce sont les preuves
d’indécidabilité et d’impossibilité. Des mathématiciens ont passé des années de leur
vie à essayer de démontrer l’hypothèse du continu, problème qui les à tourmentés
pendant très longtemps. Je me souviens d’avoir entendu dire à mon maître Polya, qui
le tenait lui-même d’Alexandroff, qu’Alexandroff avait pendant un an travaillé à la
démonstration de l’hypothèse du continu et puis qu’il avait arrêté parce qu’il se
sentait devenir fou. Il a bien fait. Alors, quand Gödel et Cohen sont venus nous dire
qu’il était inutile de nous tracasser les méninges et que jamais nous ne démontrerions
ni l’hypothèse du continu ni sa contradiction, nous avons dit :
« Ouf ! Quelle veine ! On n’aura plus à s’occuper de cet abominable problème »…
L’hypothèse du continu est indécidable
Bibliographie :
L’univers des Nombres - La Recherche/Hors Série- Août 1999
La notion d’infini de T. Gilbert et N. Rouche - ellipses
L’infini en mathématiques de N. Verdier - Dominos/Flammarion
Un, deux, trois…l’infini de G. Gamow - Dunod
Les paradoxes de l’infini de B. Bolzano - Éditions du Seuil
Théorie Axiomatique des Ensembles de J.-L. Krivine – Collection SUP/Presse Universitaire de France
Penser les mathématiques- ouvrage collectif – Éditions du Seuil
Infini des mathématiciens, infini des philosophes – ouvrage collectif sous la direction de F. Monnoyeur - BELIN
Quelques mots sur la psychologie de la mathématique pure de P. Chaslin – Essai sur la discordance
dans la psychiatrie contemporaine de G. Lantéri-Laura et M. Gros - E.PE.L.
Infini et Inconscient –Essai sur Georg Cantor de N. Charraud – ANTHROPOS
Les noms du père chez J. Lacan d’E. Porge - Point hors ligne/ érès
Dictionnaire de la Psychanalyse sous la direction de R.Chemama et B. Vandermersch- Larousse
…….
13