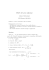Choix du bandwidth (design fix) : Le bandwidth qui minimise l`AM(I

Choix du bandwidth (design fix) :
Le bandwidth qui minimise l’AM(I)SE est de nouveau de
l’ordre n−1/5 :
¶1/5
µ 2
σ (x)R(K)
−1/5
n
,
hAM SE (x) =
′′
2
(m (x))2 µ2
et
hAM ISE =
µR
σ 2 (x) dx R(K)
R(m′′ )µ22
¶1/5
n−1/5 ,
ce qui propose, de nouveau, un estimateur de type
"plug-in" :
Celui nécessite un estimateur de σ 2 (x) et un estimateur de
′′
m (x) (voir ci-dessous).
De nouveau, l’AMSE et l’AMISE se comporte comme
∼ n−4/5 si n → ∞.
Comme dans le cas de l’estimation de densité, on peut
"accélerer" ce taux de convergence :
Si m possède r dérivées continues, et si le noyau et de
l’ordre r (au moins), le taux de convergence de l’AM(I)SE
2r
est de l’ordre n− 2r+1 et le bandwidth optimal sera de
1
l’ordre n− rs+1 .
53
Estimation des dérivées
(1) Estimation des dérivées des densités :
Un estimateur naturel de f (k) = la dérivée d’ordre k de f
est :
¶
µ
n
X
x
−
X
1
i
(k)
(k) (x) =
,
K
fd
nhk+1 i=1
h
pour un noyau qui a k dérivées.
(k) est
Si K (k) est un noyau de l’ordre 2, l’AMSE de fd
(k) (x)] =
AMSE[fd
(k)
R
1
nh2k+1
f (x) R(K
avec R(K ) = (K (k) (u))2 du et
R
(k)
µK := uk+s K (k) (u) du .
(k)
h4 k+2
(k)
(f (x))2 (µK )2
)+
4
Le bandwidth optimal qui minimise cet AMSE est de
1
l’ordre n− 2k+5 ,
et donc, le taux de convergence de l’AMSE optimal est
4
plus lent (de l’ordre n− 2k+5 ).
54
(2) Régression (désign fix, σ 2 (x) = σ 2 = constante)
Estimation de m(k) = la dérivée d’ordre k de m
Pn R si+1 (k)
−k
d
(k)
Kh (x − u) du Yi :
par m
(x,
h)
=
h
GM
i=1 si
Soit m(k) ∈ C s ([0, 1]), let K ∈ C k ([0, 1]) noyau d’ordre
k + s (c.à.d. K (k) est de l’ordre s), soit K de support
[−1, 1] (s.p.d.g.) et soient
K (j) (−1) = 0 = K (j) (1), j = 0, . . . , k − 1.
R (k)
(k)
Soit R(K ) = (K (u))2 du et
R
(k)
µK := uk+s K (k) (u) du .
Supposons que hn → 0, nhk+1
→ ∞ si n → ∞, alors
n
d
(k) (x)] =
AMSE[m
h2s
σ2
(k) 2
(k+s)
2
(x)) + 2k+1 R(K (k) ) ,
(µK ) (m
(k + s)!
nh
ce qui est la généralisation exacte du cas k = 0.
Le taux de convergence de l’AMSE est plus lent (de
2s
l’ordre n− 2k+2s+1 ).
Le bandwidth optimal qui minimise cet AMSE est de
1
l’ordre n− 2k+2s+1 .
Si l’on veut choisir le bandwidth en pratique (avec une
méthode de "plug-in") il faudrait estimer des dérivées
encore plus hautes.
De nouveau, des procedures itératives se proposent.
55
Estimateur itératif de type "plug-in"
Brockmann et al (1992): Procédure itérative pour
bandwidth et global et local (estimateur de Gasser et
Müller, design fix, σ 2 (x) = σ 2 = constante) :
• (i) Soit b
h0 = n−1 .
• (ii) Itérer
2
σ
b
R(K)
1/5
b
hi = (
)
R
c′′ (x, b
n µ22 (m
hi−1 n1/10 ))2 dx
pour i = 1, . . . , 11.
• (iii) Soit b
h=b
h11 l’estimateur de hopt
.
MISE
Pour bandwidth local : au lieu de prendre dans (ii) la
formule locale (trop peu stable), répéter (ii) pour
i = 1, . . . , 8 (étapes globales), puis ajouter deux étapes
locales (i = 9, 10) avec une version lissée par noyau pour
:
obtenir b
hopt
MSE
b
hi (x) = (
σ
b2 R(K)
1/5
)
R
c′′ (u, b
n µ22 Kbhi−1 (u − x) (m
hi−1 n1/10 ))2 du
56
Estimation de la fonction de variance
Yi = m(Xi ) + σ(Xi ) εi
i = 1, . . . , n .
Parfois (en particulier en finance) la fonction de variance
(la “volatilité") σ 2 est de l’intérêt particulier. Comment
peut-on l’estimer?
Une possibilité (Härdle et Vieu, 1992) est la suivante.
Ecrire
σ 2 (x) = IE [Y 2 |X = x] − m(x)2 ,
et remplacer IE [Y 2 |X = x] et m(x) par des estimateurs
non paramétrique (e.g. NW).
Par exemple, pour IE [Y 2 |X = x] on peut prendre
´
³
Pn
Xi −x
Yi2
i=1 K
h2
³
´
Pn
Xi −x
i=1 K
h2
et ainsi un estimateur de σ 2 (x) pourrait être
³
´
Pn
Xi −x
2
Y
i
i=1 K
h
2
³
´ −m
σ
b2 (x) = P
b 2h1 (x)
n
Xi −x
i=1 K
h2
Problème : cet estimateur n’est pas nécessairement non
négatif.
57
Autre idée (Fan et Yao, 1998) : Estimer d’abord
l’espérance conditionelle, m
b h1 (x), calculer après les
résidues, εbi = Yi − m
b h1 (Xi ), et après
´
³
Pn
Xi −x
2
ε
b
i
i=1 K
h
2
³
´
σ
b2 (x) = P
n
Xi −x
i=1 K
h2
Fan et Yao (1998) montrent que cet estimateur a une
meilleure performance.
Ceci comme alternatives aux estimateur "naifs" (Müller et
Stadtmüller, 1987) : Soit x = j0 /n.
P
σ
e2 (j0 /n) =
P
Ã
X
wj Yj0 +j
j
!2
avec j wj = 0 et j wj2 = 1 et le choix des wj tel qu’il
s’agit des différences des Yj d’ordre m = 1, 2, ....
√
√
Par exemple (m=2) : w0 = −2/ 6, w1 = w−1 = 1/ 6.
Applicable généralement, en particulier aux résidus εbi .
Evidemment, si σ 2 (x) = σ 2 = constante, utiliser
2
σ
b =
n
X
i=1
58
εb2i
La validation croisée - revisitée pour régression np
Rappel : Estimation directe du critère M(I)SE. Ici :
CV (h) = 1/n
n
X
i=1
(Yi − m
e h,−i (Xi ))2
où m
e h,−i est l’estimateur "leave-one-out"
³
´
Pn
Xj −Xi
Yi
j=1;j6=i K
h
´
³
m
e h,−i = P
Xj −Xi
n
j=1;j6=i K
h
et hCV = arg minh CV (h).
Comme dans le cas de l’estimation des densités, CV donne
un hCV trop petit et fort variable.
Version généralisée permettant aussi un calcul plus rapide:
Ã
!−1
n
n
X
X
2
(1 − Wi (Xi ))]
GCV (h) = 1/n
(Yi − m
e h (Xi ))2 ,
1/n
i=1
où Wi (x) =
i=1
Xi −x
“hX −x ”
Pn
j
j=1 K
h
K(
)
.
59