Étude du comportement des nombres flottants dans les

Étude du comportement des nombres
flottants dans les programmes C
Ali Ayad et Claude Marché
CEA List & INRIA Île-de-France
6 Octobre 2009
Ali Ayad et Claude Marché
Motivations
Vérification déductive des propriétés flottantes des
programmes C implémentant la norme IEEE-754 :
1
2
3
4
précision du calcul (erreur numérique)
division par zéro
overflows
NaNs et infinis signés
Ali Ayad et Claude Marché
Plan
1
2
3
4
Établir un langage de spécification de programmes
flottants
Établir de modèles du comportement des flottants
dans les programmes C (triplets de Hoare)
Validation des obligations de preuve qui traduisent la
spécification par une coopération des prouveurs
automatiques et interactifs
Expérimentation dans Frama-C/Jessie/Why
Ali Ayad et Claude Marché
Exemple : Approximation des fonctions
transcendantes (Algorithme de Remez)
/*@ requires \abs(x) <= 1.0 ;
@ ensures \abs(\result − \exp(x)) <= 0x1p−4 ;
@
// total error
@ */
double remezexp(double x) {
/*@ assert \abs(0.9890365552 + 1.130258690*x +
@
0.5540440796*x*x − \exp(x)) <= 0x0.FFFFp−4 ;
@
// method error
@*/
return 0.9890365552+1.130258690*x+0.5540440796*x*x ;
}
Opérations sur les réels
Variables flottantes dénotent leurs valeurs réelles
pas d’arrondi, ni overflows dans les annotations
Ali Ayad et Claude Marché
Deux modèles des opérations flottantes
Calcul flottant du standard IEEE-754.
Première composante des modèles : axiomatisation
du premier ordre de la fonction d’arrondi
Deuxième composante : modélisation des opérations
flottantes par des triplets de Hoare avec 2 options :
défensive : pas d’overflows, pas de NaNs : c’est le
cas de la plupart des programmes
full : overflows, NaNs, infinis et zéros signés
Ali Ayad et Claude Marché
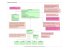
Architecture des modèles flottants
Annotated
C program
C front-end
(Frama-C)
VC generator
(Jessie/Why)
verication
conditions
Interactive proof
Automatic proof
(Coq)
(SMT provers and Gappa)
Ali Ayad et Claude Marché
FP operations,
defensive model
axiomatic model
of FP arithmetics
FP operations,
full model
Realization
in Coq
IEEE-754 : formats et représentabilité
Un nombre flottant est représenté par :
(−1)s × 1.m × 2e
où s = 0, 1 : signe
m : matisse
e : exposant
Pour de raisons formelles, un nombre flottant est un
couple d’entiers (n, e) qui représente le réel n × 2e
Un format binaire est un triplet f = (p, emin , emax )
Un nombre réel x = n × 2e est dit représentable dans
le format f (f -représentable) si
|n| < 2p
et emin ≤ e ≤ emax .
Single (binary32) : p = 24, emin = −149 et emax = 104.
Ali Ayad et Claude Marché
IEEE-754 : opérations et valeurs spéciales
5 modes d’arrondi : vers le plus proche pair, vers
+∞, vers −∞, vers 0 et vers le plus près loin de zéro.
Opérations : pour deux nombres flottants x = n1 × 2e1
et y = n2 × 2e2 , f -représentables, la multiplication
x ∗ y est l’arrondi du réel n1 × n2 × 2e1 +e2 .
Valeurs spéciales : +0, −0, +∞, −∞ et NaNs.
(+∞) + (+∞) = (+∞), 1/(+∞) = +0,
1/(−0) = −∞, (+0)/(+0) = NaN,
(−0) × (+∞) = NaN
Ali Ayad et Claude Marché
Axiomatisation du premier ordre : Flottants
génériques
// type abstrait
type gen_float
// 2 fonctions logiques d’observation
logic float_value : gen_float −> real
logic exact_value : gen_float −> real
Ali Ayad et Claude Marché
Axiomatisation du premier ordre : Formats et
Arrondis
// 3 formats possibles
type float_format = Single | Double | Quad
// 5 modes d’arrondi (norme IEEE−754)
type mode = NearestEven | Up | Down
| ToZero | NearestAway
// fonction d’arrondi
round_float : float_format, mode, real −> real
// flottant maximal représentable
max_gen_float : float_format −> real
axiom max_gen_float(Single) = (224 − 1) × 2104
axiom max _gen_float(Double) = (253 − 1) × 2971
Ali Ayad et Claude Marché
Axiomatisation du premier ordre : Axiomatisation de
l’opérateur d’arrondi
// test de non−débordement
predicate
no_overflow(f :float_format,m :mode,x :real) =
abs_real(round_float(f,m,x)) <= max_gen_float(f)
// axiomatisation de round_float
forall f :float_format. m :mode. x :real.
|x| <= max_gen_float(f) −> no_overflow(f,m,x)
forall f :float_format. m :mode. x :real. y :real.
x <= y −> round_float(f,m,x) <= round_float(f,m,y)
etc ...
Ali Ayad et Claude Marché
Autres types abstraits : valeurs spéciales
// 2 autres types
type class = Finite | Infinite | NaN
type sign = Positive | Negative
// 2 autres fonctions d’observation
logic float_class : gen_float −> class
logic float_sign : gen_float −> sign
Ali Ayad et Claude Marché
Autres prédicats utiles : valeurs spéciales
predicate is_finite(x :gen_float) =
float_class(x) = Finite
is_infinite, is_NaN, etc ...
// infinis signés : +/− infini
predicate is_plus_infinity(x :gen_float) =
is_infinite(x) and float_sign(x) = Positive
// zéros signés : −0 et +0
predicate is_gen_zero(x :gen_float) =
is_finite(x) and float_value(x) = 0.0
predicate is_gen_zero_plus(x :gen_float) =
is_gen_zero(x) and float_sign(x) = Positive
etc ...
Ali Ayad et Claude Marché
Signe d’un résultat fini
axiom finite_sign : forall x :gen_float.
is_finite(x) and float_value(x) <> 0.0 −>
same_sign_real(x,float_value(x))
predicate sign_zero_result(m :mode,x :gen_float) =
float_value(x) = 0.0 −>
(m = Down −> float_sign(x) = Negative)
and
(m <> Down −> float_sign(x) = Positive)
Ali Ayad et Claude Marché
Classe d’un résultat dans le cas d’overflow
predicate
overflow_value(f :float_format,m :mode,
x :gen_float)=
m = Down −>
float_sign(x) = Negative −> is_infinite(x)
and
float_sign(x) = Positive −> is_finite(x) and
float_value(x) = max_gen_float(f)
and
m = Up −>
float_sign(x) = Negative −> is_finite(x) and
float_value(x) = − max_gen_float(f)
and
float_sign(x) = Positive −> is_infinite(x)
Ali Ayad et Claude Marché
Classe d’un résultat dans le cas d’overflow
and
m = ToZero −> is_finite(x) and
float_sign(x) = Negative −>
float_value(x) = − max_gen_float(f)
and
float_sign(x) = Positive −>
float_value(x) = max_gen_float(f)
and
m = NearestAway or m = NearestEven −>
is_infinite(x)
Ali Ayad et Claude Marché
Realisation Coq
gappalib-coq-0.12 (Guillaume Melquiond) :
http ://gappa.gforge.inria.fr/
Record gen_float : Set := mk_gen_float {
genf : float2 ;
float_class : Float_class ;
float_sign : sign ;
sign_invariant : float_class = Finite −>
(float2R genf <> 0)%R −>
same_sign_real_bool float_sign (float2R genf) ;
float_value := float2R genf ;
exact_value : R ;
}.
Ali Ayad et Claude Marché
Rappel : Triplet de Hoare
Pour une opération f , le triplet de Hoare est défini par :
f (x1 , . . . , xn ) : {P(x1 , .., xn )} τ {Q(x1 , .., xn , result)},
l’opération f prend comme arguments x1 , . . . , xn qui
vérifient la formule logique du premier ordre P
(pré-condition) et renvoie une valeur result de type τ tel
que la formule Q(x1 , .., xn , r ) est vérifiée (post-condition).
Ali Ayad et Claude Marché
Modèle défensive : div_gen_float
parameter div_gen_float :
f :float_format −> m :mode −>
x :gen_float −> y :gen_float −>
{ float_value(y) <> 0.0
and
no_overflow(f,m,float_value(x)/float_value(y)) }
gen_float
{float_value(result) =
round_float(f,m,float_value(x)/float_value(y))
and
exact_value(result) = exact_value(x)/exact_value(y)
}
Ali Ayad et Claude Marché
Modèle défensive : Exemple
Démo : Approximation de la fonction exponentielle par
l’algorithme de Remez.
Ali Ayad et Claude Marché
Modèle full : add_gen_float
parameter add_gen_float :
f :float_format −> m :mode −>
x :gen_float −> y :gen_float −>
{ }
gen_float
{
exact_value(result)=exact_value(x)+exact_value(y)
and
is_NaN(x) or is_NaN(y) −> is_NaN(result)
Ali Ayad et Claude Marché
Modèle full : add_gen_float
and
is_finite(x) and is_infinite(y) −>
is_infinite(result) and same_sign(result,y)
and
is_infinite(x) and is_finite(y) −>
is_infinite(result) and same_sign(result,x)
and
is_infinite(x) and is_infinite(y)
and same_sign(x,y) −>
is_infinite(result) and same_sign(result,x)
and
is_infinite(x) and is_infinite(y)
and diff_sign(x,y) −> is_NaN(result)
Ali Ayad et Claude Marché
Modèle full : add_gen_float
and
is_finite(x) and is_finite(y)
and no_overflow(f,m,float_value(x)+float_value(y)) −
is_finite(result) and
float_value(result) =
round_float(f,m,float_value(x)+float_value(y))
and sign_zero_result(m,result)
and
is_finite(x) and is_finite(y)
and not no_overflow(f,m,
float_value(x)+float_value(y)) −>
samesign_real(result,float_value(x)+float_value(y))
and overflow_value(f,m,result)
}
Ali Ayad et Claude Marché
Expérimentation : arithmétique d’intervalles
Addition et multiplication des intervalles
Exemple typique : mode d’arrondi (Down), +∞ et −∞
Ali Ayad et Claude Marché
Expérimentation : arithmétique d’intervalles
Addition et multiplication des intervalles
Exemple typique : mode d’arrondi (Down), +∞ et −∞
Preuves des OPs :
Premier essaie dans Coq : dizaines des cas à
considérer !
Les OPs sont automatiquement prouvées en ajoutant
des lemmes et des assertions dans le code
Ali Ayad et Claude Marché
Conclusions et perspectives
Conclusions :
Modélisation des opérations flottantes
indépendamment du langage de programmation
L’arithmétique flottante peut être automatisée mais sa
spécification est complexe !
Faiblesse des prouveurs SMT sur les réels : besoin
d’ajouter manuellement des axiomes
Utilisation de plusieurs types de prouveurs
Perspectives :
Meilleure coopération des prouveurs automatiques et
interactifs : par exemple, utilisation des prouveurs
automatiques comme des tactiques dans Coq
Intégration de Gappa dans les prouveurs SMT
Mélanger les deux modèles défensive et full dans un
même programme.
Ali Ayad et Claude Marché