Filtrage de Kalman appliqué à un système linéaire à

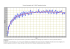
UPMC Master 2 – SSIR 2005/06
UE Informatique pour la Robotique
Filtrage de Kalman
appliqué à un système linéaire
à accélération constante.
PARTIE THEORIQUE :
Nous vous rappelons les équations du filtre de Kalman ci-dessous :
établies à partir de l’équation d’état :
où x(k) est l’état à l’instant k, u(k) est le vecteur de commande, v(k) est un bruit centré.
et en considérant l’équation de mesure :
où w(k) est un bruit gaussien centré.
PARTIE EXPERIMENTALE :
1 Description du problème
On désire estimer la position et la vitesse d'un mobile se déplaçant à accélération constante.
Cette accélération est soumise à des accélérations aléatoires (variation du régime moteur,
variation du coefficient d'adhérence,...). L'ensemble de ces accélération aléatoires sont
supposées indépendantes et de moyenne nulle. On peut donc écrire entre deux instants
d'échantillonnage de la mesure (tn≤t < tn+1) :
γ(t) = γ0+γn
E[γn] = 0
E[γnγn+k] = Γ.δk
.
1.
Écrire l'équation de récurrence donnant la vitesse x n+1 à l’échantillon tn+1 en fonction
.
de la vitesse x n à l’instant tn,γ0 l’accélération à l’instant 0, et γn un bruit gaussien sur
l’accélération de moyenne E[γn] = 0 et de variance Γ (on posera T = tn+1−tn).
2.
Écrire de même l'équation de récurrence donnant xn+1 la position à l’instant tn+1 en
fonction de xn et des variables précédentes.
3.
Montrer que la représentation d'état du système peut se mettre sous la forme (En
supposant que seule la position est accessible à la mesure et que cette mesure est bruitée par
un bruit gaussien et moyenne nulle et de variance Ω)
Xk+1 = F.Xk+Buk+Gvk
Zk = HXk+Wk
.
avec Xk = [ xk , x k ] T . Donner les matrices F, H ainsi que les vecteurs B, G, Wk et des scalaires
uk et vk ; en précédant par identification avec les équations développées dans les questions 1 et
2.
4.
5.
Programmer les équations des filtres prédicteur et estimateurs. On remarquera que les
équations sont plus simples car le système est stationnaire.
Générer un ensemble d'observations bruitées en utilisant les paramètres suivants :
T = 0.1s , γ0 = 1ms−2 , Γ = 1 , Ω = 100 , X0 = [ 0 -10 ]T
On générera la séquence d'accélérations aléatoires en utilisant la fonction randn. On
supposera par la suite que les variances de bruit d'état et de mesures nous sont inconnues.
2 Influence des conditions initiales
Pour Γ = 1 et Ω = 100, examiner l'influence du choix des conditions initiales. On
considérera les cas suivants :
Etat initial
X0 = [ 0 – 10]T
X0 = [ z0, (z1−z0)/(T) ]T
X0 = [ z0, (z1−z0)/(T) ]T
X0 = [ z0, (z1−z0)/(T) ]T
Variance initiale Λ 0
⎡0
⎢0
⎣
⎡0
⎢0
⎣
0⎤
0⎥⎦
0⎤
0⎥⎦
0 ⎤
⎡Ω
⎢ 0 4Ω / T 2 ⎥
⎣
⎦
0 ⎤
⎡Ω
100 ⎢
2⎥
⎣ 0 4Ω / T ⎦
3 Influence du choix des variances des bruits
Pour des valeurs de X0 et Λ0 bien choisies, examiner l'effet du choix arbitraire des
variances de bruit de mesure et d'état. On considérera en particulier les valeurs suivantes et on
suivra l'évolution de la variance d'erreur d'estimation sur la position.
bruit de mesure Ω
100
10000
1
100
100
10000
1
bruit d'état Γ
1
1
1
100
0.01
100
0.01