Math 220 November 8 I. Evaluate thel indefinite integral. 1. ∫ (e3x +
Transcription
Math 220 November 8 I. Evaluate thel indefinite integral. 1. ∫ (e3x +
Math 220 November 8 I. Evaluate thel indefinite integral. 1. Z (e3x + sin(3x) + tan(3x))dx 2. Z 3. 4. Z Z Z 6. x2 dx x3 + 5 √ tan( x) √ dx x Z Z sin(x) dx cos(x) csc2 (x) cot(x))dx 5. 7. (x cos(x2 )dx x2 sin(x3 + 1)dx 8. Z x dx 1 + x2 9. Z x dx 1 + 16x4 10. Z √ x 3 − xdx 11. Z √ x3 x2 − 1dx II. Evaluate the integral. 1 1. 1 Z 2 xe−x dx 0 2. π Z x3 sin(x)dx −π 3. 1 x dx 1 + x4 1 √ t t + 1dt Z 0 4. Z 0 5. Z π/4 tan(x)dx 0 6. Z π/2 sin(2x) + cos(4x)dx 0 2 1 Solutions I. Evaluate thel indefinite integral. 1. Z (e3x + sin(3x) + tan(3x))dx Answer: Z (e3x + sin(3x) + tan(3x))dx = u = 3x du = 3dx 1 du = dx 3 Z 1 (eu + sin(u) + tan(u)) du 3 Z Z 1 1 = (eu + sin(u))du + tan(u)du 3 3 Z 1 u 1 sin(u) = (e − cos(u)) + du 3 3 cos(u) = w = cos(u) dw = − sin(u)du = = = = 2. Z 1 1 u −1 (e − cos(u)) + dw 3 3 w 1 u 1 (e − cos(u)) + (− ln |w|) + C 3 3 1 1 u (e − cos(u)) + (− ln | cos(u)|) + C 3 3 1 3x −1 (e − cos(3x)) + (ln | cos(3x)|) + C 3 3 Z (x cos(x2 )dx 3 Answer: Z (x cos(x2 )dx = u = x2 du = 2xdx Z = 1 cos(u) du 2 1 sin(u) + C 2 1 = sin(x2 ) + C 2 = 3. Z sin(x) dx cos(x) Answer: Z sin(x) dx = cos(x) u = cos(x) du = − sin(x)dx −1 du u = − ln |u| + C = − ln | cos(x)| + C Z = 4. Z csc2 (x) cot(x))dx 4 Answer: Z Z 2 csc (x) cot(x))dx = csc(x)(csc(x) cot(x))dx u = csc(x) du = − csc(x) cot(x)dx Z = u(−du) Z = − udu −u2 +C 2 − csc2 (x) +C = 2 = 5. Z x2 dx x3 + 5 Answer: Z x2 dx = x3 + 5 u = x3 + 5 du = 3x2 dx Z = 11 du u3 1 ln |u| + C 3 ln |x3 + 5| = +C 3 = 6. Z √ tan( x) √ dx x 5 Answer: Z √ tan( x) √ dx = x u= √ x 1 du = √ dx 2 x Z = tan(u)2du = −2 ln | cos(u)| + C √ = −2 ln | cos( x)| + C 7. Z x2 sin(x3 + 1)dx Answer: Z x2 sin(x3 + 1)dx = u = x3 + 1 du = 3x2 dx Z 1 sin(u) du 3 −1 cos(u) + C = 3 −1 = cos(x3 + 1) + C 3 = 8. Z x dx 1 + x2 Answer: Z x dx = 1 + x2 u = 1 + x2 du = 2xdx Z = 11 du u2 1 ln |u| + C 2 ln |1 + x2 | = +C 2 = 6 9. Z x dx 1 + 16x4 Answer: Z x dx = 1 + 16x4 = = Z u = 4x2 du = 8xdx Z = x dx 1 + (4x2 )2 1 1 du 1 + u2 8 1 tan−1 (u) + C 8 1 = tan−1 (4x2 ) + C 8 = 10. Z √ x 3 − xdx Answer: Z √ x 3 − xdx = u=3−x x=3−u du = −dx Z = Z = √ (3 − u) udu (3u1/2 − u3/2 )du u3/2 u5/2 − +C 3/2 5/2 2 = 2u3/2 − u5/2 + C 5 2 = 2(3 − x)3/2 − (3 − x)5/2 + C 5 =3 11. Z √ x3 x2 − 1dx 7 Answer: Z x 3 √ Z x2 − 1dx = √ x2 x2 − 1xdx u = x2 − 1 x2 = u − 1 du = 2xdx √ 1 (u − 1) u du 2 Z 1 = u3/2 − u1/2 du 2 1 u5/2 u3/2 − )+C = ( 2 5/2 3/2 1 1 = (x2 − 1)5/2 − (x2 − 1)3/2 + C 5 3 Z = II. Evaluate the integral. 1. Z 1 2 xe−x dx 0 Answer: Z 1 2 xe−x dx = u = −x2 0 du = −2xdx Z u(1) = eu u(0) = = = = 2. −1 du 2 Z −1 −1 u e du 2 0 −1 −1 (e − e0 ) 2 −1 −1 (e − 1) 2 1 1 − 2 2e Z π x3 sin(x)dx −π 8 Answer: Z π x3 sin(x)dx = 0 −π Since x3 sin(x) is odd. 3. 1 Z 0 x dx 1 + x4 Answer: Z 0 1 x dx = 1 + x4 Z 0 1 x dx 1 + (x2 )2 u = x2 du = 2xdx Z u(1) = u(0) Z 1 1 1 dx 1 + u2 2 1 1 dx 2 0 1 + u2 1 = (tan−1 (1) − tan−1 (0)) 2 1 π = ( − 0) 2 4 π = 8 = 4. Z 1 √ t t + 1dt 0 9 Answer: Z 1 √ t t + 1dt = u=t+1 0 t=u−1 du = dt Z u(1) = √ (u − 1) udu u(0) 2 Z = u3/2 − u1/2 du 1 u5/2 u3/2 i2 − = 5/2 3/2 1 2√ 2√ 2 2 =( 32 − 8) − ( − ) 5 3 5 3 2 √ 2 √ = ( 32 − 1) − ( 8 − 1) 5 3 5. Z π/4 tan(x)dx 0 Answer: Z π/2 iπ/4 tan(x)dx = − ln(cos(x)) 0 0 = − ln(cos(π/4)) − (− ln(cos(0)) √ = − ln(1/ 2) + ln(1) = − ln(2−1/2 ) ln(2) = 2 6. Z π/2 sin(2x) + cos(4x)dx 0 10 Answer: Z π/2 Z π/2 sin(2x) + cos(4x)dx = 0 Z sin(2x)dx + 0 π/2 cos(4x)dx 0 iπ/2 1 iπ/2 1 = (− cos(2x)) + sin(4x) 2 4 0 0 1 1 = (− cos(π) + cos(0)) + (sin(2π) − sin(0)) 2 4 1 1 = (1 + 1) + (0 − 0) 2 4 =1 11
Documents pareils
Question posée : Calculer ∑ k=0 cos(kx). En utilisant une formule
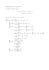 Question posée : Calculer
Question posée : Calculer


 Differentiation Formulas
Differentiation Formulas


 Tabla de Integrales
Tabla de Integrales
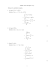

 csc u cot udu 2csc u 2csc
csc u cot udu 2csc u 2csc





![MATH 141 Fundamental Theorem of Calculus (FTC) Let f : [a, b] → R MATH 141 Fundamental Theorem of Calculus (FTC) Let f : [a, b] → R](http://s1.doczz.fr/store/data/000158037_1-90738254df74b2352f400181e26e259f-70x70.png)

