Fiche_Dynamique_Vibratoire

Transcription

Résolution approchée de problèmes de dynamique
en régime permanent
F. Louf
Dans cette fiche, on montre comment calculer une solution approchée à un problème de
dynamique en régime permanent à l’aide de la méthode des éléments finis. L’étude sera
menée sur une barre en traction. La procédure pour mener un tel calcul dans Catia est
présentée.
1 Démarche générale
La démarche ressemble fortement à celle proposée au chapitre ??. Puisque, dans le cas général, il n’est pas possible de calculer les modes propres et fréquences propres exactes, nous
commençons par calculer une base modale approchée par la méthode des éléments finis. On
obtient alors, contrairement au modèle continu, un nombre fini Nddl de modes propres. En pratique, pour une structure complexe, on se limite à nombre de modes bien inférieur au nombre
de degrés de liberté.
Le calcul de la solution par superposition modale, consiste donc à chercher la solution sous la
forme (dans le cas unidimensionel) :
u(x, t) =
N
ddl
X
φn (x)gn (t)
n=1
Cela nécessite ensuite de résoudre des équations différentielles découplées en gn (t), ici en
nombre fini, où apparaissent au second membre les efforts imposés projetés dans la base modale. Nous verrons qu’il est possible de résoudre exactement ces équations différentielles sous
l’hypothèse, peu contraignante en pratique, d’efforts imposés linéaires par morceaux.
Dans la suite, nous illustrons cette méthode sur l’exemple de la barre en traction, soumise à un
effort en bout, de type « échelon ».
2 Rappel du problème continu
x=L
x=0
~x
F IG . 1 – La barre et les conditions aux limites
La structure étudiée dans ce chapitre est unidimensionnelle. Il s’agit d’une barre soumise à
un chargement de traction compression. Ses caractéristiques géométriques et matériau sont
notées :
– L : longueur ;
– S : section ;
– E : module d’Young ;
– ρ : masse volumique.
On note u(x, t) le déplacement d’un point d’abscisse x de la barre à l’instant t. La figure 1
présente la structure dans son environnement. Le déplacement, en x = 0, est imposé nul :
u(0, t) = 0
∀t ∈ [0, T ]
où [0, T ] représente l’intervalle temporel d’étude. Le chargement est appliqué en bout de
– Calcul dynamique dans Catia – Eléments de théorie - F. Louf
2
poutre. On le note F (t). On obtient alors :
∂2u
∂2u
−
ρS
= 0 ∀x ∈ [0, L] ∀t ∈ [0, T ]
∂x2
∂t2
∂u
u(0, t) = 0 et ES (L, t) = F (t) ∀t ∈ [0, T ]
∂x
∂u
u(x, 0) = 0 et
(x, 0) = 0 ∀x ∈ [0, L]
∂t
ES
(1)
(2)
(3)
3 Formulation variationnelle
On suit la démarche classique. Pour éviter toute confusion avec le champ de vitesse, on note
le champ test u∗ . Le problème posé est alors équivalent à :
Z L 2
Z L 2
∂ u ∗
∂ u ∗
ES
u dx = ρS
u dx ∀u∗
(4)
2
2
∂x
∂t
0
0
∂u
(5)
u(0, t) = 0 et ES (L, t) = F (t) ∀t ∈ [0, T ]
∂x
∂u
(x, 0) = 0 ∀x ∈ [0, L]
(6)
u(x, 0) = 0 et
∂t
En intégrant par partie, et en utilisant la relation entre déplacement et effort imposé en x = L,
on obtient la formulation variationnelle suivante :
∀u∗ /u∗ (0, t) = 0
∗
F (t)u (L) = ES
Z
L
0
∂u ∂u∗
dx + ρS
∂x ∂x
Z
L
0
u(0, t) = 0 ∀t ∈ [0, T ]
∂u
u(x, 0) = 0 et
(x, 0) = 0 ∀x ∈ [0, L]
∂t
∂2u ∗
u dx
∂t2
(7)
(8)
(9)
4 Discrétisation par éléments finis
4.1 Choix du maillage
On divise le domaine [0, L] en N segments à deux nœuds de taille identique. On exprime alors
le champ de déplacement recherché à l’aide des fonctions de base éléments finis :
u(x, t) = [N(x)]{u(t)}
(10)
Le vecteur {u(t)} représente les valeurs aux nœuds du champ de déplacement à l’instant t. On
choisit u∗ (x, t) de la même forme :
u∗ (x, t) = [N(x)]{u∗ (t)}
(11)
4.2 Discrétisation des équations d’équilibre
En poursuivant la démarche classiquement utilisée pour des problèmes ne faisant pas intervenir
le temps, on introduit u(x, t) et u∗ (x, t) de la forme choisie dans la formulation variationnelle.
3
Avant toute chose, il faut définir :
∂u∗
∂u
′
(x, t) = [N (x)]{u(t)} et
(x, t) = [N ′ (x)]{u∗ (t)}
∂x
∂x
∂2u
(x, t) = [N(x)]{ü(t)}
∂t2
(12)
(13)
L’équation (7) devient alors :
T
∗
T
T
∗
F (t){u (t)} [N(L)] ={u (t)} ES
Z
0
∗
T
+ {u (t)} ρS
L
[N ′ (x)]T [N ′ (x)]dx{u(t)}
Z
L
[N(x)]T [N(x)]dx{ü(t)}
(14)
0
On nomme respectivement K, M, {F (t)}, les matrices de raideurs, de masse, et le vecteur des
forces généralisées définis par :
Z L
K = ES
[N ′ (x)]T [N ′ (x)]dx
{F (t)} = [N(L)]T F (t)
(15)
0
Z L
M = ρS
[N(x)]T [N(x)]dx
(16)
0
Le problème est donc de trouver le vecteur {u(t)} avec [N(0)]{u(t)} = 0, vérifiant, ∀{u∗ (t)} :
h
i
(17)
{u∗ (t)}T K{u(t)} + M{ü(t)} − {F (t)} = 0
[N(0)]{u(t)} = 0 ∀t ∈ [0, T ]
{u(0)} = {0} et {u̇(0)} = {0}
(18)
(19)
En conséquence, cela nous permet de nous ramener à la résolution de N + 1 équations différentielles couplées, sur tout l’intervalle d’étude :
M{ü(t)} + K{u(t)} = {F (t)}
u(0, t) = [N(0)]{u(t)} = 0 ∀t ∈ [0, T ]
{u(0)} = {0} et {u̇(0)} = {0}
5 Calcul des modes approchés
5.1 Recherche de solutions synchrones
On recherche tout d’abord les solutions de l’équation d’équilibre éléments finis homogène de
type :
u(x, t) = g(t)[N(x)]{φ}
(20)
soit encore :
{u(t)} = g(t){φ}
(21)
En injectant cette forme de solution dans l’équation d’équilibre éléments finis homogène on
obtient :
M{φ}g ′′ (t) + K{φ}g(t) = 0
(22)
4
5.2 Obtention des pulsations propres et des modes propres
soit encore
−
g ′′ (t)
M{φ} = K{φ}
g(t)
(23)
Montrons que la constante λ définie par :
λ=
g ′′ (t)
g(t)
(24)
est réelle et négative. Dans le cas général où le mode propre {φ} est complexe, {φ} = {a} +
i{b}, on obtient :
−λM {a} + i({b} = K {a} + i{b}
(25)
En pré-multipliant cette dernière équation par {φ} = {a} − i{b}, on trouve :
−λ {a}T − i{b}T M {a} + i{b} = {a}T − i{b}T K {a} + i{b}
λ=−
{a}T K{a} + {b}T K{b}
{a}T M{a} + {b}T M{b}
(26)
(27)
Les matrices K et M sont symétriques et positives. Par conséquent l’expression précédente
implique que la constante λ est réelle et négative. On pose donc λ = −ω 2 .
5.2 Obtention des pulsations propres et des modes propres
Les pulsations propres sont les ωn telles que les solutions du système linéaire suivant soient
non-triviales :
(K − ω 2 M){φ} = {0}
(28)
où {φ} doit toujours vérifier des conditions aux limites. En effet, celles-ci n’ont pas encore été
prises en compte. Dans le cas où elles sont homogènes, il suffit d’éliminer dans les matrices
K et M les lignes et colonnes associées aux degrés de liberté bloqués. Dans le cas présent,
on éliminera la première ligne et la première colonne. Les matrices K et M de dimensions
e et M
f de dimensions N × N.
(N + 1) × (N + 1) deviennent donc les matrices K
Les pulsations propres ωn sont alors telles que les solutions du système linéaire suivant soient
non-triviales :
e − ω 2 M){
f φ}
e = {0}
(K
(29)
n
et donc telles que :
e − ω 2 M)|
f =0
|K
n
(30)
e − ω 2 M){
f φen } = {0}
(K
n
(31)
Les pulsations propres ωn du modèle éléments finis sont donc les N racines réelles et positives
d’un polynôme de degré 2N en ω. Comme dans le cas continu, on les range dans un ordre
croissant.
Une fois que les ωn sont calculées, il reste à calculer les vecteurs {φen } tels que :
Le vecteur {φ} s’obtient alors sans difficulté à partir de {φen } en tenant compte de la condition
en x = 0.
5
5.3 Orthogonalité
5.3 Orthogonalité
Comme pour un système continu, deux modes distincts sont orthogonaux. Soient deux modes
distincts {φn } et {φp }. Par définition, ils vérifient :
(K − ωn2 M){φn } = {0}
(K − ωp2 M){φp } = {0}
(32)
(33)
En pré-multipliant (32) par {φp }T et (33) par {φn }T , et en faisant la différence des équations
obtenues on obtient :
{φp }T K{φn } − {φn }T K{φp } = ωn2 {φp }T M{φn } − ωp2 {φn }T M{φp }
(34)
La transposée d’une matrice 1 × 1 étant cette même matrice, on a :
{φp }T K{φn } = {φn }T KT {φp }
{φp }T M{φn } = {φn }T MT {φp }
(35)
(36)
Enfin, puisque les matrices de raideur et de masse sont symétriques :
0 = (ωn2 − ωp2 ){φn }T M{φp }
(37)
Les modes n et p étant par hypothèse distincts, l’équation précédente conduit à :
{φn }T M{φp } = 0 pour n 6= p
(38)
ce qui montre que les modes n et p sont orthogonaux. On en déduit immédiatement que :
{φn }T K{φp } = 0 pour n 6= p
(39)
5.4 Masse modale et raideur modale
On définit la masse modale Mn et la raideur modale Kn par :
Mn = {φn }T M{φn }
(40)
Kn = {φn }T K{φn }
(41)
(K − ωn2 M){φn } = {0}
(42)
{φn }T K{φn } = ωn2 {φn }T M{φn }
(43)
Le mode {φn } vérifie :
et donc :
On obtient immédiatement la relation :
ωn2 =
Kn
Mn
(44)
6
5.5 Normalisation
5.5 Normalisation
Comme dans le problème continu, on peut choisir φn tels que :
– le vecteur propre {φn } soit de norme unitaire ;
– la masse modale associée Mn soit unitaire ;
– la raideur modale associée Kn soit unitaire.
5.6 Mise en œuvre
On considère un maillage simple constitué de 3 segments à deux nœuds. Le nombre de degré
de liberté est donc égal à 4.
5.6.1 Calcul des matrices K et M
On commence par calculer les matrices élémentaires Ke et Me qui valent :
"
#
Z Le
ES
ES
1
−1
Ke = e
[N ′ (x)]T [N ′ (x)]dx = e
L 0
L −1 1
"
#
Z Le
1/3
1/6
Me = ρSLe
[N(x)]T [N(x)]dx = ρSLe
1/6 1/3
0
(45)
(46)
Par assemblage, on obtient les matrices K et M de dimensions 4 × 4, avec Le = L/N = L/3 :

1

3ES −1
K=

L 0
0

1/3

ρSL 1/6
M=

3  0
0

−1 0
0
2 −1 0 


−1 2 −1
0 −1 1

1/6 0
0
2/3 1/6 0 


1/6 2/3 1/6
0 1/6 1/3
(47)
(48)
5.6.2 Prise en compte des conditions aux limites
La condition aux limites, en x = 0 étant homogène, il suffit d’éliminer la première ligne et la
première colonne des matrices de masse et de raideur :


2 −1 0

e = 3ES 
(49)
K
−1 2 −1
L
0 −1 1


2/3 1/6 0

f = ρSL 
(50)
M
1/6 2/3 1/6
3
0 1/6 1/3
7
5.6 Mise en œuvre
5.6.3 Calcul des pulsations propres
e − ω2M
f:
Calculons le déterminant de K
2
6c2 − 2ω2 − 3c22 − ω2
0
L
9
L
18
2
2
2
2
2
2
6c
2ω
3c
ω e − ω 2M|
f = 0 ⇔ − 3c2 − ω
|K
−
−
−
=0
18
L2
9
L2
18 L
2
2
2
2
ω
3c
ω
3c
− 9 0
− L2 − 18
L2
(51)
On obtient donc l’équation :
a3 − 2ab2 = a(a2 − 3b2 ) = a(a −
√
3b)(a +
√
3b) = 0
(52)
en ayant posé :
6c2 2ω 2
−
L2
9
2
3c
ω2
b=− 2 −
L
18
a=
(53)
(54)
Les pulsations propres sont donc les solutions positives de :
6c2 2ω 2
−
=0
L2
9
√
√
√
(6 − 3 3)c2 (4 + 3)ω 2
−
=0
a − 3b = 0 ⇔
2
L√
18
√
√
(6 + 3 3)c2 (4 − 3)ω 2
−
=0
a + 3b = 0 ⇔
L2
18
a=0⇔
(55)
(56)
(57)
On obtient finalement les trois pulsations propres données dans le tableau 1 rangées par ordre
croissant. La comparaison avec les pulsations exactes calculées via le modèle continu permet
de calculer les pourcentages d’erreur commises.
Pulsation
Estimée
s
√
c
6−3 3
√
3 2
L
4+ 3
c √
3 3
sL
√
c
6+3 3
√
3 2
L
4− 3
ω1
ω2
ω3
Exacte
cπ
L2
c 3π
L 2
c 5π
L 2
Erreur
1, 1%
9, 3%
16, 7%
TAB . 1 – Pulsations estimées par éléments finis, à l’aide d’un maillage à 3 éléments, comparées
aux pulsations exactes obtenues.
5.6.4 Calcul des modes propres
Le mode propre {φen } associé à la valeur propre ωn vérifie :
e − ω 2 M){
f φen } = {0}
(K
n
(58)
8
5.6 Mise en œuvre
Calcul de {φ1 }
Explicitons les termes a et b :
√
√
6c2 2ω12
6c2 18c2 6 − 3 3
c2 18 3
√ = 2
√
a= 2 −
= 2 − 2
L
9
L
L 4+ 3
L 4+ 3
√
c2 18
3c2
c2 6 − 3 3
3c2 ω12
√ =− 2
√
=− 2 − 2
b=− 2 −
L
18
L
L 4+ 3
L 4+ 3
Le système à résoudre devient alors :
√
   
2
3 −1 0 
 
 0

 φ1 
√


3
3 −1  φ1 = 0
−1
√ 
 
 

 4
0
φ1
0 −2
3
(59)
(60)
(61)
Bien-entendu, les équations du système ne sont pas indépendantes. On peut, par exemple fixer
φ41 = 2. Rappelons que φ11 = 0. On obtient alors :
 
0 




 1 

{φ1 } = √
(62)


3



 

2
Calcul de {φ2 }
6c2 2 27c2
6c2 2ω22
−
=
−
=0
L2
9
L2
9 L2
3c2
c2 27
c2 9
3c2 ω 2
=− 2
b=− 2 − 2 =− 2 − 2
L
18
L
L 18
L 2
   

2
0 −1 0 

 
 0
φ2 


3
=
0
φ
−1
0
−1


2

 
 

 4
φ2
0
0 −1 0
a=
On peut, par exemple fixer φ42 = 2. Rappelons que φ12 = 0. On obtient alors :
 
0




2

{φ2 } =

0



 

−2
Calcul de {φ3 }
(63)
(64)
(65)
(66)
√
√
6c2 2ω32
6c2 18c2 6 + 3 3
c2 18 3
√ =− 2
√
a= 2 −
= 2 − 2
L
9
L
L 4− 3
L 4− 3
√
c2 18
3c2
c2 6 + 3 3
3c2 ω32
√ =− 2
√
=− 2 − 2
b=− 2 −
L
18
L
L 4− 3
L 4− 3
√
   
2
3 1
0 
 φ3 
 
 0

√


3
3 1  φ3 = 0
 1
√ 
 4
 
 

φ3
0
2
3
0
(67)
(68)
(69)
9
5.6 Mise en œuvre
Bien-entendu, les équations du système ne sont pas indépendantes. On peut, par exemple fixer
φ43 = 1. Rappelons que φ13 = 0. On obtient alors :


0





 1 

√
{φ3 } =

3
−






2
(70)
Tracé des modes On a représenté les trois modes calculés précédemment sur la figure 2. Ces
modes sont à comparer aux modes exacts tracés sur la figure 3.
2
1
1.5
-1
2
2.5
3
3.5
4
Mode 1
Mode 2
Mode 3
-2
F IG . 2 – Les trois modes calculés par éléments finis
1.0
0.5
0.2
-0.5
0.4
0.6
0.8
1
Mode 1
Mode 2
Mode 3
-1.0
F IG . 3 – Les quatre premiers modes pour une barre de longueur unitaire
10
6 Fonctions de réponse en fréquence
6.1 Définition
La fonction de réponse en fréquence représente l’amplitude du déplacement d’un point d’abscisse x = x1 du domaine [0, L] en fonction de la fréquence d’excitation imposée en un point
x = x0 . On la note H(x1 , x0 , ω). Ici, on propose de les déterminer de façon approchée, à l’aide
du calcul des modes et pulsations propres déjà effectué.
6.2 Calcul des FRF
Nous avons vu que l’équation d’équilibre éléments finis est de la forme :
M{ü(t)} + K{u(t)} = {F (t)}
(71)
On cherche le vecteur des déplacements nodaux solution de la forme :
{u(t)} =
N
X
n=1
{φn }gn (t)
(72)
En injectant cette solution type dans l’équation d’équilibre éléments finis, on obtient :
N
X
n=1
M{φn }gn′′ (t)
+
N
X
n=1
K{φn }gn (t) = {F (t)}
(73)
En pré-multipliant cette dernière équation par le vecteur {φp }T , et en utilisant la propriété
d’orthogonalité des modes, il vient :
Mn gn′′ (t) + Kn gn (t) = {φn }T {F (t)}
pour n ∈ {1, ..., N}
(74)
pour n ∈ {1, ..., N}
(75)
pour n ∈ {1, ..., N}
(76)
Puisque Mn ωn2 = Kn , on trouve :
gn′′ (t) + ωn2 gn (t) =
1
{φn }T {F (t)}
Mn
Ecrivons la transformée de Laplace de cette équation :
Gn (p)[p2 + ωn2 ] =
1
{φn }T {F (p)}
Mn
De plus, puisque la transformée de Laplace de {u(t)} est :
{U(p)} =
il vient :
N
X
n=1
{φn }Gn (p)
N
X
{φn }{φn }T
{U(p)} =
{F (p)}
Mn (p2 + ωn2 )
n=1
(77)
(78)
que l’on peut encore écrire sous la forme :
{U(p)} = Q(p){F (p)}
(79)
11
6.3 Tracé des fonctions de réponse en fréquence
En remplaçant p par iω, on obtient la matrice des fonctions de transfert :
{U(p)} = H(ω){F (p)}
(80)
La matrice H est de dimensions N × N, et symétrique de par sa définition. Le coefficient
Hi,j (ω) représente l’effet sur le déplacement du nœud i de la barre d’une excitation au nœud
j, à la pulsation ω, et inversement.
Remarque. – Rappelons que dans le modèle continu, la fonction H(x, x0 , ω) représentait l’effet sur le déplacement du point d’abscisse x de la barre d’une excitation au point d’abscisse
x0 , à la pulsation ω
Afin de comparer les résultats à ceux obtenus via le modèle continu, on maille tout d’abord la
barre avec 5 éléments de sorte que le point d’abscisse L/5 coincide avec un nœud, le troisième
en l’occurence. Le point d’excitation en x = L coïncide avec le dernier et sixième nœud. On
comparera donc H(L/5, L, ω) et H3,6 (ω), ainsi que H(L, L, ω) et H6,6 (ω). Les résultats sont
donnés sur la figure 4. On se limite volontairement à une pulsation comprise entre le huitième
et le neuvième mode.
Naturellement, puisque seuls cinq degrés de liberté existent, le nombre de modes visibles sur
les fonctions de réponse en fréquence H6,6 (ω) et H3,6 (ω) ne peut excéder 5.
12
FRF exacte
FRF estimée
1.4
1.2
1.0
0.8
0.6
0.4
0.2
5
10
15
20
25
(a) Fonctions de réponse en fréquence H(L, L, ω) et H6,6 (ω)
FRF exacte
FRF estimée
1.4
1.2
1.0
0.8
0.6
0.4
0.2
5
10
15
20
25
(b) Fonctions de réponse en fréquence H( 2L
5 , L, ω) et H3,6 (ω)
F IG . 4 – Tracé des FRF H6,6 (ω) et H3,6 (ω) (Maillage à 5 éléments)
13
FRF exacte
FRF estimée
1.4
1.2
1.0
0.8
0.6
0.4
0.2
5
10
15
20
25
(a) Fonction de réponse en fréquence H(L, L, ω) et H20,20 (ω)
FRF exacte
FRF estimée
1.4
1.2
1.0
0.8
0.6
0.4
0.2
5
10
15
20
25
(b) Fonction de réponse en fréquence H( 2L
5 , L, ω) et H9,20 (ω)
F IG . 5 – Tracé des FRF estimées H20,20 (ω) et H9,20 (ω) (Maillage à 20 éléments)
On constate de plus, comme lors de l’étude du modèle continu, que le nœud 3, d’abscisse
14
2L/5 est un nœud de vibration pour le troisième mode, et que par conséquent celui-ci n’est
pas visible sur le tracé de H3,6 (ω).
Sur la figure 5, les fonctions de réponses en fréquences similaires obtenues pour un maillage à
20 éléments sont tracées.
Naturellement, cette fois, les 9 premiers modes approchés sont visibles, excepté sur le tracé de
H9,20 (ω) où les modes 3 et 9 disparaissent, le neuvième nœud d’abscisse 2L/5 étant un nœud
de vibration pour ces modes. Le calcul des pulsations et modes propres basse fréquence étant
plus précis, les FRF approchées et exactes sont plus proches.
Enfin, ces figures mettent de nouveau en évidence le fait que les fréquences propres calculées
par éléments finis sont une sur-estimation des fréquences propres exactes.
7 En pratique dans Catia
On suppose ici que le maillage, les propriétés et matériaux de la structure étudiée sont déjà
définis.
7.1 Calcul de la base modale
Pour commencer, il faut calculer la base modale :
– Insérer un Cas de fréquence à partir du menu Insertion et laisser cochée la case Conditions
aux limites ;
– Préciser les conditions aux limites ;
– En double cliquant sur la Solution Modale contenue dans le Cas de fréquences, préciser le
nombre de modes à calculer, c’est-à-dire la taille de la base dans laquelle on cherchera la
réponse dynamique dans la suite ; bien évidemment, ce nombre de modes ne peut excéder
le nombre de degrés de liberté du problème éléments finis.
7.2 Définition du chargement
Ensuite, il faut définir la zone et le contenu fréquentiel du chargement. La zone est définie dans
un Cas statique qu’il n’est pas nécessaire de calculer, le contenu fréquentiel est celui d’un bruit
blanc.
– Insérer un Cas statique à partir du menu Insertion ; si l’on veut, on peut faire pointer les
conditions aux limites vers celles du Cas de fréquences ;
– Créer le chargement du type souhaité : force surfacique, distribuée, ou autre, selon le type
de modèle utilisé.
7.3 Calcul de la réponse en régime permanent
Enfin, il faut définir le calcul de dynamique vibratoire : base modale utilisée, chargement
(direction, zone d’application, type, et contenu fréquentiel), amortissement.
– Insérer un Cas de réponse dynamique à partir du menu Insertion ; préciser que la base modale utilisée est celle contenue dans le Cas de fréquences ;
15
7.4 Post traitement
– Insérer une modulation en fréquence de type Bruit blanc ou particulière via un fichier à
deux colonnes du type de celui présenté dans le tableau 2 ; les fréquences repérées ne sont
pas forcément régulièrement espacés ;
– En double cliquant sur Excitation des charges, dans la fenêtre qui apparaît :
– préciser le chargement à exciter en cliquant dans l’arbre sur le chargement défini dans le
cas statique ;
– préciser la modulation en fréquence en cliquant sur la modulation en fréquence insérée
précédemment (elle se trouve sous le noeud Modulations de l’arbre.
– En double cliquant sur Amortissement dans l’arbre, on peut préciser le type d’amortissement
et le coefficient d’amortissement retenu ; par défaut l’amortissement est modal et la valeur
donnée est identique pour chaque mode : 1%.
– En double cliquant sur Solution de réponse dynamique harmonique dans l’arbre, préciser la
bande de fréquence étudiée, et le pas de calcul fréquentiel à utiliser.
Remarque. – On aurait pu insérer plusieurs chargements dans un cas statique et définir plusieurs modulations associées.
f(Hz)
0
100
100
1000
1000
F
0
0
1
1
0
TAB . 2 – Exemple de fichier donnant la modulation fréquentielle de l’effort imposé : cas d’un
filtre de type carré
7.4 Post traitement
Le post traitement peut se faire de différentes façons :
– il est toujours possible de générer une image (cliquer droit sur Solution de réponse dynamique transitoire puis Génération d’images) présentant les déplacements, vitesses, accélérations, contraintes, etc et de spécifier dans la fenêtre ouverte l’Occurence, c’est à dire
l’instant auquel on souhaite représenter le champ choisi ;
– il est également possible de tracer l’évolution fréquentielle d’une quantité de type déplacement, vitesse, accélération ; pour cela, cliquer droit sur Solution de réponse dynamique et
choisir Générer un affichage 2D ; dans la fenêtre qui s’ouvre :
– cliquer sur fin
– puis dans la fenêtre Sélection de données, choisir le(s) degré(s) de liberté à tracer : sélectionner le noeud souhaité sur le maillage qui s’affiche dans la fenêtre de calcul (fichier
.CATAnalysis) et préciser la ou les directions à tracer ;
16
7.5 Comparaison
– dans l’onglet configuration, préciser si l’on souhaite tracer le déplacement, la vitesse ou
l’accélération ;
– dans la fenêtre d’affichage 2D, un graphique est tracé : il est possible de modifier les axes
(échelles, titres, etc) en double cliquant dessus ;
– on peut ensuite exporter la courbe au format texte (cliquer droit, puis choisir exporter).
7.5 Comparaison
Une comparaison a été effectuée entre différents calculs éléments finis et une fonction de
réponse en fréquence de référence obtenue via un modèle continu non amorti. Les différents
calculs éléments finis correspondent à :
– un maillage à trois éléments et une base modale contenant les trois premiers modes ;
– un maillage à 50 éléments et une base modale contenant les trois premiers modes ;
– un maillage à 50 éléments et une base modale contenant les dix premiers modes.
La figure 6 montre la convergence des FRF éléments finis vers la FRF issue du modèle continu
(l’amortissement est ici faible, et ne change pas la solution de manière notable, hormis les
amplitudes).
F IG . 6 – Evolutions du déplacement en bout en fonction de la fréquence : solutions approchées
obtenues avec différents maillages et tailles de base modale, solution exacte non-amorti
17
7.5 Comparaison
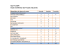
Icône
Nom de l’outil
Description sommaire
Force distribuée
Appliquer une force en N de façon distribuée sur un support
Pression
Appliquer une pression en N/m2 sur une surface
Encastrement
Bloquer tous les ddl d’un support
Glissement surfacique
Bloquer tous les ddl selon la normale à un support
Contraintes avancées
Bloquer les ddl choisis d’un support
Bruit blanc
Préciser le contenu fréquentiel de l’effort
Modulation fréquentielle importée Préciser le contenu fréquentiel de l’effort via un fichier
Calcul
Lancer le calcul de toutes ou d’une partie des analyses
Animation
Animer le tracé d’un champ dépendant du temps
TAB . 3 – Outils utilisés dans Catia et icônes correspondantes dans les ateliers utilisés
18

Fiche_Dynamique_Vibratoire

Transcription

Documents pareils

CATIA V5 INITIATION

CATIA V5-Intégration V4 et interopérabilité (V5-V4I)

dessinateur mecanique catia v5 h/f

DESSINATEUR/PROJETEUR AERONAUTIQUE CATIA V4/V5 H/F

Dessinateur projeteur Catia V5 H_F

Catia Veglia Bio

DESSINATEUR en CONSTRUCTION MECANIQUE

Un Dessinateur / Projeteur Mécanique CATIA V5

Bac Pro EDPI

technico-commercial technicien superieur de commerce