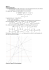Correction du Devoir à la maison N°3 Exercice 1 1 x ⃗ AM(a+1 AM

Correction du Devoir à la maison N°3
Exercice 1
Dans un repère orthonormé ( O; ⃗
i ;⃗
j ) , on considère le point A ( −1 ;−1 ) et les droites d 1 et d 2
d'équations respectives y=1 et x=1 .
Soit M un point variable sur la droite d 1 . On appelle N le point d'intersection éventuel des
droites ( AM ) et d 2 et P le milieu du segment [ MN ] .
La conjecture sur Géogébra permet de dire que le point P semble être sur l'hyperbole y=
1
x
On a le point M qui se trouve sur la droite d 1 qui a pour équation y=1 , donc comme le point
M varie sur la droite d 1 il a pour coordonnée M ( a ;1 ) avec a ∈ℝ
Si a=−1 alors ( AM ) a pour équation x=−1 .
Si a≠−1 déterminons une équation de la droite ( AM ) .
⃗
AM a+1
1+1
AM ( a+1 ) est un vecteur directeur de la droite ( AM )
( ) soit ⃗
2
Donc la droite ( AM ) a pour début d'équation 2 x−( a +1 ) y +c=0
A∈ ( AM ) donc 2×(−1 )−( a +1 ) ×(−1 ) +c=0⇔−2+a +1+c=0 ⇔ c=−a+1
Donc ( AM ) a pour équation 2 x−( a +1 ) y−a+1=0
Si a=−1 alors ( AM ) et d 2 ne se coupent pas car les deux droites sont parallèles, donc N
n'existe pas, et donc P n'existe pas non plus.
Si a≠−1 , le point N est le point d'intersection de la droite ( AM ) et de la droite d 2 , donc
N ( x ; y ) vérifie :
−a+ 3
−a +3
2 x−( a+ 1 ) y−a +1=0 ⇔ 2−( a +1 ) y−a+1=0 ⇔ y =
, donc N 1 ;
a
+1
a +1
x=1
x=1
x=1
−a +3
4
1+
1+a
a+1
1+a a+1
;
;
Le point P est le milieu de [ MN ] , donc P
, P
2
2
2
2
1
Donc P est un point de l'hyperbole H d'équation y=
x
Lorsque M décrit la droite d 1 le point P décrit l'hyperbole
{
{
{
(
(
) (
)
)
EXERCICE 2
ABCDEFGH est un cube et I est le milieu de [ FB ] .
1. et 2. Voir figure.
1
1
1
3. ⃗
EI =⃗
EA+ ⃗
AB+ ⃗
BI =⃗
EA+ ⃗
AB+ ⃗
BF =⃗
EA+ ⃗
AB− ⃗
EA= ⃗
EA+ ⃗
AB
2
2
2
⃗
⃗
⃗
⃗
⃗
⃗
⃗
⃗
⃗
⃗
EL= EA+ AD+ DL= EA+ AD+ 2 DC + DA= EA+ 2 AB
EL=2 ⃗
EI , donc E , L et I sont alignés (et même
Donc ⃗
mieux I est le milieu de [ EL ] ).
1
1
4. ⃗
GI =⃗
GF + ⃗
FI =⃗
DA+ ⃗
FB=⃗
DA+ ⃗
EA et
2
2
⃗
GM =⃗
GH + ⃗
HD+ ⃗
DM =−⃗
DC+ ⃗
EA+ ⃗
DC + 2 ⃗
DA=⃗
EA+ 2 ⃗
DA
⃗
⃗
Donc GM =2 GI , donc G , I et M sont alignés (et
même mieux I est le milieu de [ GM ] ).
5. Première méthode :
I est le milieu de [ EL ] et [ GM ] donc EGLM est un
ML sont
parallélogramme, donc les vecteurs ⃗
EG et ⃗
égaux.
Deuxième méthode : ⃗
EG=⃗
AC (cube) et
⃗
ML=⃗
MD+ ⃗
DL=−⃗
DC −2⃗
DA+ 2⃗
DC + ⃗
DA=⃗
DC −⃗
DA=⃗
DC + ⃗
AD=⃗
AD + ⃗
DC =⃗
AC
⃗
⃗
Donc les vecteurs EG et ML sont égaux.
, P
(
1+a
2
;
2
a +1
)