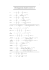dérivées usuelles - Les pages perso du Crans

D ÉRIVÉES USUELLES
Fonction
Dérivée
Domaine de validité
x 7−→ f [ u(x) ]
x 7−→ u0 (x) f 0 [ u(x) ]
selon Du et Df
x 7−→ nxn−1
R
x 7−→ 2αx + β
R
x 7−→ pxp−1
] − ∞, 0[ ou ]0, +∞[
(n ∈ N∗ )
x 7−→ xn
x 7−→ αx2 + βx + γ
(n ∈ R∗ )
x 7−→ xp
a
x 7−→ [u(x)]
1
x
1
x 7−→ n
x
x 7−→
1
u(x)
√
x 7−→ x
x 7−→
x 7−→
p
u(x)
(a ∈ R∗ )
a−1
x 7−→ a u0 (x) [u(x)]
x 7−→
−n
−1
x2
1
xn+1
−u0 (x)
u(x)2
1
x 7−→ √
2 x
x 7−→
u0 (x)
x 7−→ p
2 u(x)
selon Du
] − ∞, 0[ ou ]0, +∞[
R
{x ∈ Du ; u(x) 6= 0}
]0, +∞[
{x ∈ Du ; u(x) > 0}
x 7−→ ln x
x 7−→
1
x
]0, +∞[
x 7−→ ln u(x)
x 7−→
u0 (x)
u(x)
{x ∈ Du ; u(x) > 0}
x 7−→ ex
x 7−→ ex
R
x 7−→ ax
x 7−→ (ln a) ax
R
x 7−→ eu(x)
x 7−→ u0 (x) eu(x)
Du
x 7−→ sin x
x 7−→ cos x = sin (x +
x 7−→ cos x
x 7−→ tan x
x 7−→ arcsin x
x 7−→ arccos x
x 7−→ arctan x
π
)
2
π
x 7−→ − sin x = cos (x + )
2
1
= 1 + tan2 x
x 7−→
cos2 x
1
1 − x2
−1
x 7−→ √
1 − x2
1
x 7−→
1 + x2
x 7−→ √
R
R
−π π
,
2 2
] − 1, 1[
] − 1, 1[
R
x 7−→ sh x
x 7−→ ch x
R
x 7−→ ch x
x 7−→ sh x
R
x 7−→ th x
x 7−→
x 7−→ arg sh
x 7−→ √
x 7−→ arg ch
x 7−→ arg th
1
= 1 − th2 x
ch2 x
1
1 + x2
1
x 7−→ √
2
x −1
1
x 7−→
1 − x2
R
R
]1, +∞[
] − 1, 1[
+ πZ