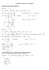Fiche de révisions n°1 : Les nombres complexes

M. JACQUIER
BTS IRIS
T.D. N°1 : LES NO MBRES COMPLEXES 1
EXERCICE 1
Déterminer le module et l'argument de chacun des nombres complexes :
1. z1 = -1 + i 3
2. z2 = 1 + cos q + i sin q
EXERCICE 2
Calculer le nombre z = (2 - 3i)(1 + 2i)(3 - 2i)(2 + i)
EXERCICE 3
k étant un nombre réel donné, mettre sous la forme a + ib le nombre z =
1 + ki
.
2k + (k2 - 1)i
EXERCICE 4
Déterminer le module et l'argument du nombre complexe z =
1+i 3
.
3+i
EXERCICE 5
1
On donne z1 = ( 6 - i 2) et z2 = 1 - i.
2
Déterminer le module et l'argument de Z =
z1
.
z2
Exprimer Z sous la forme algébrique.
En déduire les valeurs de cos
p
p
et sin .
12
12
EXERCICE 6
Montrer que la formule de Moivre est valable pour n entier négatif.
EXERCICE 7
A partir de l'égalité cos q =
eiq + e-iq
linéariser cos4 q, c'est-à-dire exprimer cos4 q comme combinaison
2
linéaire de sinus et cosinus des arcs multiples de q.
EXERCICE 8
Déterminer les racines quatrièmes de i.
EXERCICE 9
Calculer les racines carrées du nombre complexe 5 + 12i.
EXERCICE 10
1. Résoudre dans ℂ l'équation z2 = 5 + 12 i.
2. Résoudre dans ℂ l'équation z2 - (1 + i 3)z - 1 + i 3 = 0.
EXERCICE 11
On considère la transformation définie par z' = 2 iz + 2 + i.
Montrer que la transformation géométrique T associée admet un point invariant A d'affixe a.
Exprimer z' - a et en déduire la nature de T.
EXERCICE 12
Le plan complexe P est rapporté à un repère orthonormal (O ; Å
u, Å
v ). On désigne par A et B les points
d'affixes respectives i et -2. A tout point M de P, distinct de A, d'affixe z, on associe le point M' d'affixe z'
défini par :
z' =
z+2
.
z-i
1. On note I le milieu du segment [AB]. Déterminer l'affixe du point I' associé à I.
2. On pose z = x + iy et z' = x' + iy'
avec x, y, x', y' réels.
a) Déterminer x' et y' en fonction de x et y.
b) Déterminer et tracer l'ensemble E des points M d'affixes z tels que z' soit réel.
c) En interprétant géométriquement l'argument de z', montrer que si z' est réel alors M, A, B sont alignés.
EXERCICE 13
q est un nombre réel donné.
1. Résoudre dans ℂ l'équation d'inconnue Z : Z2 - 2 Z cos q + 1 = 0.
En déduire la résolution dans ℂ de l'équation d'inconnue z :
z4 - 2 z2 cos q + 1 = 0.
(E)
(Les racines seront présentées sous forme trigonométrique.)
2. Dans le plan complexe on considère les images M1 , M2, M3 et M4 des quatre racines de (E).
Pour quelle valeur de q (0 < q < p) ces quatre points sont-ils les sommets d'un carré ?
3. Décomposer en un produit de deux facteurs du second degré et à coefficients réels le polynôme défini
par : f (x) = x4 - 2 x2 cos q + 1.
EXERCICE 14
On considère la transformation géométrique définie par z' =
1. Montrer que z' = 2 -
2z - 3
.
z-1
1
.
z-1
2. En déduire que z' s'obtient à partir de z au moyen des transformations définies par z1 = z - 1, z2 =
z3 = -z2, z' = 2 + z3.
Caractériser chacune des transformations.
3. Dans un repère (O ; Å
u, Å
v ) tracer le point M' image de z' à partir de la donnée du point M image de z.
1
,
z1