Etude d`un pendule élastique vertical Détermination de la constante

Terminale S – TP de Physique n°12b
Mécanique
Etude d’un pendule élastique vertical
Détermination de la constante de raideur d’un ressort (correction)
Objectif : utiliser deux méthodes expérimentales pour déterminer la constante de raideur k d’un ressort.
On considère un pendule élastique constitué d’un solide
de masse m et d’un ressort de constante k (exprimée en
N.m–1), de longueur à vide Lo et de masse négligeable
devant m.
La raideur d’un ressort traduit sa réponse à la
déformation ; dans la suite, on se place dans le cadre de
la loi de Hooke1 pour laquelle k ne dépend pas de la

charge m : la force de rappel F du ressort est alors
proportionnelle à son élongation.


F  k   L


où  L  x i d’après les conventions ci-contre. Ecarté de sa
position d’équilibre, le système oscille entre les positions
symétriques –xm et xm.
1 – Méthode statique
On suspend une masse m au ressort de raideur k. Le ressort, de longueur à vide Lo, s’allonge d’une
longueur ΔL = Lo – Lc où Lc est la longueur du ressort à l’équilibre après la charge. A l’équilibre, le




poids P  m  g et la force de rappel élastique F   k L  i se compensent, ce qui conduit à l’égalité
m g  k L
–2
avec g = 9,81 m.s l’intensité du champ de pesanteur terrestre. Cette relation n’est vérifiée que dans le
domaine d’élasticité du ressort, où la loi de linéarité de Hooke s’applique : c’est pourquoi, dans notre
cas, il ne faudra pas dépasser mmax = 300 g.
Pour m = mmax, on relève une élongation ΔLmax = 7,4 cm.
1. En déduire une valeur de la constante de raideur k du ressort : k 
m g 0,300  9,81

 40 N .m 1
2
7, 4.10
L
2. Donner une méthode simple permettant d’augmenter la précision obtenue sur k.
L’utilisation de plusieurs masses marquées, inférieures à 300 g, permettrait d’obtenir plusieurs valeurs
de k dont on pourrait faire la moyenne…
2 – Méthode dynamique
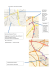
On réalise le montage de la figure suivante (document 1). La masse de l’aiguille est m1 = 8,0 g ; la masse
marquée m2 variable peut osciller librement et sans frottement notable dans l’éprouvette remplie d’une
solution aqueuse de sulfate de cuivre (II). Initialement, la pointe de l’aiguille est centrée entre les deux
électrodes en cuivre.
Lorsque le système oscille verticalement, la tension u(t) mesurée entre la masse et la pointe de l’aiguille
est proportionnelle à x(t), écart du centre d’inertie de la masse marquée par rapport à la position
d’équilibre.
On notera M = m1 + m2.
L’équation différentielle du mouvement est donnée par l’application de la 2ème loi de Newton à
l’ensemble {masse marquée + aiguille} de masse M,
1
Du nom du britannique Robert Hooke (1635-1703) qui fut l’un des plus grands expérimentateurs du XVIIème siècle. En
1660, il énonce la loi d’élasticité qui porte aujourd’hui son nom : « ut tension sic vis », telle extension, telle force.
2
  

Fext  P  F  M a


En projetant ici sur l’axe (Ox) dirigé par i , il vient



M g i  k x i  M 
xi
et l’équation différentielle sur la position x(t),
k

x
xg
M
On reconnaît la forme générale 
x  o 2 x  cte
k
la pulsation propre de
M
l’oscillateur. Les solutions sont des fonctions
sinusoïdales plus ou moins amorties (en fonction
des frottements) dont l’expression théorique de la
période propre est
2
M
To 
 2
o
K
avec o 
Document n°1
5 To
En faisant varier m2, on peut relever différentes valeurs de période To par acquisition, comme indiqué
sur le document n°2 :
m2 (kg)
0,100
0,150
0,200
0,250
0,300
M (kg)
0,108
0,158
0,208
0,258
0,308
5 To (s)
1,635
1,965
2,245
2,490
2,715
To (s)
0,327
0,393
0,449
0,498
0,543
0,107
0,154
0,202
0,248
0,295
To2
2
(s )
1. Remplir le tableau.
2. Tracer les variations de To2 en fonction de M. Quelle est l’allure du graphe ? Conclure.
3
Les points se répartissent visiblement suivant une droite passant par l’origine. En effet, en utilisant
l’expression théorique de To, il vient
2
M
To 
 2
o
K
M
To 2  4 2
K
2
 4 
To 2  
 M
 K 
To² = f(M)
To² (s²)
0,35
0,3
0,25
0,2
To² = 0,9645 x M
R2 = 0,9992
0,15
0,1
0,05
M (kg)
0
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
3. Proposer une modélisation par régression de To2 = f(M).
Cf. graphe précédent.
4. En utilisant l’expression théorique de To, donner l’expression de la constante de raideur k en
fonction de To et de M. En déduire une valeur de k.
2
M
To 
 2
o
K
M
To 2  4 2
K
M
K  4 2  2
To
4 2
4 2
 0,965 s 2 .kg 1 conduit à K 
 40,9 N .m 1
K
0,965
5. Comparer les résultats des deux méthodes, statique et dynamique
Les résultats obtenus sont tout à fait comparables, à condition de tenir compte d’un ensemble statistique
de mesures.
A.N. :