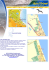
Part2Chap1 - Etienne Roquain`s

Elements de
cutie
I
Estimation
:
double muddle line
Chapitre
Chapitne
1
:
2
:
Chapitre 3
:
Introduction
Selection de modete
stohishquemdthimah.queengeandeowmensianematietienne.roquain@upmc.frR0QUAINE.P
(
)
dimension
ain
deyeende
Portie I
:
Estimator
LASSO
Tests
Goheginirale
( testeplnsiuers
ai
hyp
ein
melees
)
Chapitn
1
Chapitk
2
Chapitre
Introduction
:
3
:
:
Control
Control
du
du
taux
dinner
par
fan ; lle
tauxdefauxposikfs
!1!
test
Motivation
3apµ
simple
dragibus
"
Ho
:
pas
entre
di association
&
Of
Statistique
si
tel
test
de
1
Rejetde
)
SK
Ho
>
"
duegibwsenacne
niveaeed
an
ca
SK )
que
,
)
CLEIR
sup
Po
0€00
Ibis
)
p
Ho
pcx )
&
{
obs
=
niveaeed
an
p value
L
{
.
p=inf}dC[qr]
pour
ca
>
nsquedetypet
Rejetde
si
(
SK
x
=
Xlw
sup Pg (
OEOO
)
SK
:
>
ca
)
SK )
>
Sex )
)
}
Test
multiple ?
Ii
Propniti
(
TD 4
Exo 1
p
w
v
(
o
,
1)
P
alas
ou
Ho
sous
)
( pet
t
pour
E
domination
stoahestique
)
paruneueoi uniform
et
1-
[ 0,1 ]
(1
.
0.05
)m
design
^
Hole mullipliciti
si
m
f
)
9
pas
'
pi
tri
,
probabiliti
P(
→
longue
tie
.
.
posikf
U
(
}
,m
1
Pied
:
an
quond
moins
nb
)
=
1
faux
tests z
-
1)
o
-
proba de faire
=
iid
m
trower quelque chose
de
31 ,
m
(t
,
:
-
Am
>
un
100
TD
4 Ex
.
2
Pi } )
L(inf{
nsicm
m
Donnie
weelles
expression de
m
gives pour
n
imlividus
yum
indite
→
I
gwupe
(
Sain
But
:
trouvergines
different iellementexprimis
)
1
test
par
gene
Grande dimension
grouped
( malade
)
Cia
Beaucoup de gives
↳ beaucoup detests
"
given
gene
z
9
2
variable
1
=
1
give
pen
de
ie
mn)
'
a
faire
105
petitions
n
2102
!
Autre dowries
Neurounaye
arecphin
:
regions
detests
actives
?
!
Economic
:
ogagnantes
strategies
Astronomic
directions
?
:
avec
une
Etoile
?
Model general
!2!
Definition
*
:
models
sous
modele
le
hypotheses Willes
general puree tests de
30,1 }m
( configuration des hypotheses vneieslfausscs
HE
:c
constant
est
m
It
'
=
o
⇐ >
'
a
partier:
ieinghypothief
dunefamilledelois
dlunparamithe
Vjc
Pt
/
*
p=(
et
tel
pour
que
tout
,
.
.
( bscoordonnies
Notations
:
Pg
,m
.
Hj=o
}
avec
correspondent
'
a
H
=
0
Pn
}icj<
1
m
1
12 13 P4
:
01
Ps
Hj
0
PG
=
o
,
P( Pj
et
)
des hypotheses vneics
tensemble des indices correspondent
HOCH )
(
)
t.cj.cm
,
lois compatibles
area
H
)
Ft
HPE
}r
pour
vines
}
et
cardinal
son
1
0
17 Ps Pg Pro
Pj
out des pvalues
Pm
1
1
Pm Th }
y
0
10
10
mo(
0
0
Prs Pro RF Rs
Pn "
Ulo
est
,
1)
)
H
tE[gs]
sous
.
uniform
note
est
hypotheses
aux
pour tout
t
{
0
Bos
=/
WH
0
0
1
)
/
1
0
Ro Rn Pzz R3R4
)
ttjem
Pj
H
(
,
0
)
tjfm
Pj
1
Pn
1
1
Pz
B
01
P4
Ps
PG
1
0
0
P7 Ps
Pos
Pu Pm Th }
Pro
10
10
0
avec
:
.
.
#
pour
,
.
.
.
=
}
O=
Hj=o
}
,m
-0
Of
.
0
1
0
avec
(
H
,P )
HE 30,Hm
:
,
on
,
,
PEPH
}
Qo =P
a
Identifiable .tt
Lemme
Prove
:
H¥Hi%nPj=¢
lemodileest
identifiable
Ssi
HH
,
HE
0
Vjc
f
( H ,P )
1
R7R8R9RoRnRzR3R4
tPcFt
:
) NQO
,
0
0
1)
,
}r
(
0
Prs Pro
Pn "
Ulo
y
Pj
Reformulation
1
1
}o,Hm
,
avec
PC Piet )
{
t
pour tout
tE[gD
H
des
Close
:
homogeires
independents
10
10
p.s.j.CH
modelers
Examples
pj=o
0
1
1
Pn
12
B
Definition
( pi
Examples
:
,
.
.
.
detest
0
Ps
P4
Soit
:
lemodefe
el
01
Fi
P7 Ps Pg
sous
un
Pro
)
110066 iid
-
Pu Pm Th }
0
0
'
associi
a
uniform
unilateral
Hj=o
Fzlt
( pi
,
{ (
pi
,
pour
)=1il3o
Elt )=
§(
tout
IETCOCH )
}
)
;¢wa+) )
( pj
j
Ulps )
iidn
Fs
.lHI
.
S
)
'
ou
S
)
Gaussian bilateral
TD4Exo4
ElH=
ECOEHTH
.
s
)
+
moyenne
EFEFHI
.
s
'
( pas
( signals
TD4Exo3
.
EF
,^ ) )
icjcnniiidwlo
,
,s]
o
HE 391 }m
iid
(
OETH
[
0
R3R4
Pzz
sur
estoknnipar
I
1
0
1
0
0
repartition
fonckons de
independent
area
0
R7R8R9 Ro Rn
Prs Pro
Pn "
de
dame
ensemble
-
Uniform
Gaussian
1
1
multiple independent homogine
nsiem
Dirac
PG
1
0
)
des
(
→
designate)
to
)
alternatives
£=1
.
#
)
litres examples
(
Hodde
.
l
forcer
sans
'
independence
)
unilateral
,
pour
XN
W(Hµ
,
5)
pour
gaussian
)
,
M£4995 }
0=1 Hoi )
done
TD4Exo4
Hodde
bilateral
.
connuefj-1Ft-3LkoIllxgHlg.anxnNlHy.r1.ye@MTldonc0-CHfx.ModefeissudetestsperpeunutationTD4Exo5.Modeeidiotdedipendenumaximafe.U
tD4Exo3Definilionlemodelegaussienunihetinel@ecolipenohenaconnuxesto6finiparpj-0IlXgD.1ej.com
[email protected]
Definition
bilateral
pj=2§(
¥1
le modele
)
,
gaussian
iejcm
,
pour
dependence
avec
XN
W(Hµ
,
5)
est defini
commie
?
µf(R*
Hf3o,Hm
pour
NUH
,
1)
,
ttjf
par
)
,
}
'
,
.
.
,m
}
,
malice
5
Pj
-
U
et
mxm
Hj=o
.
!3!
Procedure
Definition
procedure detest
une
.
:
multiple
variables
^
de la
H
forma
( II
.
pour
la
1
=
variable
une
On note souvenir R
de
.
ma
pour
Pcs )
On
les
£
vase
nine
3
=
an
is
generate
,
jam
Lm
procedures per seuillaye
PG )
5
.
.
restneindre
f
.
aux
}
Ilp )
.
j
=
r
}
est
define par
Ilp ) }
pjs
hypotheses
I
:
)
ngitee
Hp ) ER
11
les
rgitte
m
^
aliatoire
=
391 }
ieine hypothec est
procedure detest multiple de sent
(
.
la
⇐ >
Hfcp )
.
( ifjlp ) } game
=
aliatoires
unefamillede
est
avec
1
,
une
p
.
<
value
( ensemble de rgit
possibilities pour
ej
de
:
e
E
m
)
Elp )
)
#
?
Pan )
procedures per
→
seulemeut
mts
seuillages dens
possibilities
he
an
suite
,
plus
Definition
.
TTE
30,1T
et
I
et
H
€30
fjfm
^
Hf
:
faux psikf
=
faux nigakf
ejcm
1
=
ole
eueur
vmeie
Paradigm
:
=L
tTj=o
Hj
,
}
=o
=
Hj
,
fauve
1
=
alarm
=o
Hj
#
1
=
FAUX
VRAI
NEGATIF
POSITIF
est
Hj=
}
=
fausse detection
=
de
euenr
type
1
FAUX
VRAI
NEGATIF
POSITIF
I
type I
dicouvute
de
#
est
faux nigahfs
faussediwunihe
=
Him
.
=o
einsemkedes
{
vreiposihfs
pour
:
I
type
linsembledesfauxposihfs
{
.
de
Events
!4!
=
vneie
alarm
Neyman Pearson
e
=
:
vmeie
detection
1
Controller
he
a
Sachaut
1
quonliti
.
06
faux psihfs
maxi
miser
de
vmeis
la
queen
posikfs
an
lite
nine
2
Chaix
du
said
?
Neyman Pearson
PC
E
Pcs)
:
such
an
pw
true
de
f
.
.
faux psihfs
:
<
.
,
sent
pay
G
plus guard possible
>
R
guedes
vneisposikfs
sfaux osihfs
maisdapantage
devneispsitifs
:
unfaux
posit
choisir
?
Lieahefascondemesurerlacyuanlitedefauxposihfs
.
Chap
2
:
auaenfaeexpositfs
pwbas
avec
.
Chap 3
:
f-
,
[
1-
a
nbfauxposihfs
"
bpsitfs
)
5
X
Different regimes
signal
§
force
foible
pour
6
signal
guendefora
quantities
elite
quenhteevuemaonhti