Développements en séries entières usuels
Transcription
Développements en séries entières usuels
Formulaire PanaMaths (CPGE) Développements en séries entières usuels Fonction Développement en série entière (DSE) Intervalle de validité du DSE +∞ xn x 2 x3 = 1 + x + + + ... ∑ 2 6 n=0 n ! \ x 6 chx x2n x2 x4 x6 = 1 + + + + ... ∑ 2 24 720 n = 0 ( 2n ) ! \ x 6 shx x 2 n +1 x3 x5 x7 x = + + + + ... ∑ 6 120 5040 n = 0 ( 2 n + 1) ! \ x6e x +∞ +∞ ( −1) x 2 n = 1 − x 2 + x 4 − x 6 + ... ∑ 2 24 720 ( 2n ) ! n =0 n +∞ ( −1) x 2 n+1 = x − x3 + x5 − x 7 + ... ∑ 6 120 5040 n = 0 ( 2n + 1) ! n +∞ x 6 cos x x 6 sin x x 6 (1 + x ) α Où α ∈ \ 1 1− x 1 x6 1 − x2 1 x6 1+ x 1 x6 1 + x2 +∞ α (α − 1)(α − 2 ) ... (α − ( n − 1) ) n =1 n! 1+ ∑ +∞ ∑x x6 x6 x6 1 1 − x2 1 1 + x2 PanaMaths xn = 1 + x 2 + x 4 + x 6 + ... ]−1; +1[ x n = 1 − x + x 2 − x3 + ... ]−1; +1[ x 2 n = 1 − x 2 + x 4 − x 6 + ... ]−1; +1[ 2n n =0 ∑ ( −1) n n =0 +∞ ∑ ( −1) n ]−1; +1[ ]−1; +1[ +∞ +∞ \ = 1 + x + x 2 + x3 + ... n n =0 ∑x \ n =0 ( 2n )! x 2 n = 1 + x 2 + 3x 4 + 5 x 6 + ... ∑ 2 2n 2 8 16 n = 0 2 ( n !) n +∞ ( −1) ( 2n )! x 2 n = 1 − x 2 + 3x 4 − 5 x 6 + ... ∑ 2 2n 2 8 16 n = 0 2 ( n !) +∞ [1-2] ]−1; +1[ ]−1; +1[ Janvier 2010 +∞ x 6 ln (1 − x ) xn x 2 x3 x 4 = − x − − − − ... 2 3 4 n ]−1; +1[ x 2 n +1 x3 x5 x 7 = 1 + + + + ... ∑ 3 5 7 n = 0 2n + 1 ]−1; +1[ −∑ n =1 +∞ x 6 arg tanh x +∞ x 6 ln (1 + x ) ∑ ( −1) n n =1 +∞ ∑ ( −1) x 6 arctan x n =0 n +1 n xn = x− x 2 x3 x 4 + − + ... 2 3 4 x 2 n +1 x3 x5 x 7 = x − + − + ... 2n + 1 3 5 7 ( 2n )! x 2 n+1 = x + x3 + 3x5 + 5 x 7 + ... 2 2n 6 40 112 n=0 ( n !) 2n + 1 x3 3 x5 π +∞ ( 2n ) ! x 2 n +1 π −∑ = −x− − − ... 2 n =0 22 n ( n !)2 2n + 1 2 6 40 n +∞ ( −1) ( 2n )! x 2 n+1 = x − x3 + 3x5 − 5 x 7 + ... ∑ 2 2n 2n + 1 6 40 112 n = 0 2 ( n !) +∞ x 6 arcsin x x 6 arccos x x 6 arg sinh x PanaMaths ∑2 [2-2] ]−1; +1[ ]−1; +1[ ]−1; +1[ ]−1; +1[ ]−1; +1[ Janvier 2010
Documents pareils
Diff and Integ Rules Final
 csc u cot u du csc u C
tan u du ln sec u C ln cos u C
cot u du ln csc u C ln sin u C
sec u du ln sec u tan u C ln sec u tan u C
csc u du ln csc...
csc u cot u du csc u C
tan u du ln sec u C ln cos u C
cot u du ln csc u C ln sin u C
sec u du ln sec u tan u C ln sec u tan u C
csc u du ln csc...

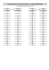

 DERIVATIVES AND INTEGRALS
Basic Differentiation Rules
DERIVATIVES AND INTEGRALS
Basic Differentiation Rules


