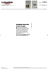La base de Frenet
Transcription
La base de Frenet
La base de Frenet Si on repère un point M par son abscisse curviligne s le long de sa trajectoire, on peut introduire la − →− → base (orthonormée) de Frenet ( T , N ) en 2D (en 3D, on prendrait un troisième vecteur pour avoir une base − → → − − → orthonormée directe) avec T tangent à la trajectoire dans le sens du mouvement,et N orthogonal à T dirigé vers l’intérieur de la concavité de la courbe. On introduit également le cercle tangent, qui est le cercle qui approche au mieux la trajectoire autour de la position actuelle de M, et on note R > 0 son rayon. Il est important de comprendre que toutes ces grandeurs varient au cours du temps. − → T M R − → N s O La vitesse de M vaut simplement → − → − v = ṡ T − → −̇ → → vecteur tangent à la trajectoire et de norme ṡ. On dérive pour avoir l’accélération : − a = s̈ T + ṡ T . −̇ → Pour calculer T , on va s’intéresser à ce qui se passe entre t et t + dt. Entre ces deux instants, le point a avancé d’une distance ṡdt. Or il se déplace approximativement sur le cercle tangent, qui a pour rayon R, donc sa direction a tourné d’un angle dθ = ṡdt R (car la longueur d’un arc de cercle est égale au produit du rayon par l’angle). Faisons alors un schéma des vecteurs à t et à t + dt (on déplace les vecteurs pour qu’ils aient la même origine). M(t) − → T (t) dθ → − T (t) − → T (t + dt) − → N (t) dθ − → T (t + dt) − → N (t) − → − → − → On voit que T (t + dt) = cos(dθ) T (t) + sin(dθ) N (t). Comme dθ est très petit devant 1, on sait que sin(dθ) = dθ et cos(dθ) = 1 à l’ordre 1 (la dérivée de cos en 0 vaut 0, donc il n’y a pas de terme en dθ). − → − → − → Donc T (t + dt) = T (t) + dθ N (t), d’où on tire − → − → ṡ − −̇ → T (t + dt) − T (t) → T = = N (t) dt R en utilisant le fait que dθ = On en déduit alors que Lycée Claude Fauriel - St Étienne ṡdt R . → v k2 → → − → k− − → − ṡ2 − → − N a = s̈ T + N = s̈ T + R R 1