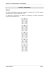Casanova : un comportement d`agent respectant la privacité

Casanova : un comportement d’agent
respectant la privacité pour des mariages
stables et équitables
Patricia Everaere 1 , Maxime Morge 1 , Gauthier Picard 2
1. Laboratoire d’Informatique Fondamentale de Lille, Université Lille 1, France
{patricia.everaere,maxime.morge}@univ-lille1.fr
2. Département ISCOD / Institut Henri Fayol
École Nationale Supérieure des Mines de Saint-Etienne, France
[email protected]
RÉSUMÉ. Cet
article prône une approche orientée individu pour la résolution du problème classique des mariages stables. Selon cette approche, la solution émerge de négociations entre
agents. L’agentification de l’algorithme séminal de Gale-Shapley revient à distinguer deux
comportements d’agents (proposant et disposant) qui négocient pour aboutir à une solution
stable mais inéquitable. Le comportement d’agent Casanova que nous proposons ici consiste à
jouer simultanément ces deux rôles dans une multitude de négociations bilatérales. Les agents
mettent en œuvre une stratégie de concession minimale maximisant leur bien-être individuel.
Les solutions qui émergent sont équitables et elles ne peuvent pas être atteintes par les méthodes multi-agents existantes. De plus, notre résolution est décentralisée et elle préserve la
privacité des préférences.
ABSTRACT. This paper promotes an individual-based approach for solving a well-known problem,
the stable marriage problem. In this approach, a solution is the output of an emergent phenomena due to the negotiation between the agents. The agentification of the seminal Gale-Shapley
algorithm is based upon two distinct behaviours (the proposer and the responder) negotiating
to reach a stable matching which is not fair. The Casanova agent behaviour we propose in
this paper relies on a society of agents that play at the same time both of these roles in multi
bi-lateral negotiations. The agents applies the minimal concession strategy for negotiation to
ensure their individual welfare. The emergent solutions are fair and they cannot be reached by
classical multi-agent methods, whereas Casanova is decentralized and privacy-preserving.
MOTS-CLÉS : système
multi-agents, modèle de comportements d’agents, résolution décentralisée,
gestion des conflits.
KEYWORDS: multiagent
systems, agent behaviour, decentralized problem solving, conflict hand-
ling.
c 2012 Lavoisier
DOI:10.3166/RIA.26.471-494 Revue d’intelligence artificielle – no 5/2012, 471-494
472
RIA. Volume 26 – no 5/2012
1. Introduction
Les systèmes multi-agents proposent un cadre conceptuel et des outils informatiques particulièrement adaptés à la modélisation et la simulation de phénomènes
complexes observés en physique, en biologie ou en économie (Schelling, 1978). L’approche orientée individu fait intervenir différentes entités en interaction dont le comportement constitue un modèle explicatif de phénomènes émergents.
Nous nous intéressons dans cet article à un problème bien connu en informatique (Knuth, 1971) et en économie (Roth, Oliveira Sotomayor, 1990), celui des mariages stables – en anglais, Stable Marriage Problem (SM). L’enjeu de ce problème
est simple. En considérant deux communautés dont chaque membre a des préférences
vis-à-vis des individus de l’autre communauté, l’objectif est de former des couples en
prenant en compte leurs préférences. Ce problème abstrait a de nombreuses applications. Par exemple, pour affecter des projets à des étudiants, chaque étudiant classe
par ordre de préférence les projets et réciproquement le responsable de chaque projet
classe lui aussi les candidats potentiels. Le covoiturage, l’échange de domicile ou les
réseaux d’entreprises sont d’autres exemples de domaines d’applications.
L’algorithme séminal de Gale-Shapley (Gale, Shapley, 1962) est une preuve constructive de l’existence d’une solution admissible pour n’importe quelle instance de
SM. L’agentification de cet algorithme proposé par Brito et Meseguer (2005) consiste
à distinguer deux comportements d’agents distincts : une communauté de proposants
et une communauté de disposants. Ainsi, les négociations entre ces agents aboutissent
à une solution stable mais inéquitable : la communauté des proposants est favorisée.
Dans cet article, nous proposons la méthode Casanova où les agents jouent simultanément le rôle de disposant et de proposant dans une multitude de négociations
bilatérales. Notre approche fait émerger des solutions stables qui ne peuvent être atteintes par les méthodes multiagents existantes (Brito, Meseguer, 2005 ; 2007) et qui
sont plus équitables entre les deux communautés. Notre résolution est décentralisée
et préserve la privacité : les agents ne communiqent pas leur préférences. Cet article
est une version étendue de (Everaere et al., 2011) où nous raffinons nos métriques et
l’évaluation de Casanova. À cette intention, nous avons réimplémenté Casanova, les
méthodes multi-agents, ainsi que les algorithmes centralisés existants (Zavidovique et
al., 2005 ; Gelain et al., 2010) dans le même langage afin de comparer les solutions
obtenues, notamment leur équité, ainsi que la complexité communicationnelle.
Nous commençons cet article par une formalisation du problème SM puis nous
présentons l’algorithme de Gale-Shapley dans une perspective orientée individu dans
la section 2. Afin d’évaluer les solutions à un problème SM nous utilisons la théorie
des jeux et la théorie du choix social, en section 3. Notre méthode Casanova est décrite
dans la section 4. Nous passons en revue les approches existantes pour la résolution de
problèmes SM, en section 5. Nous présentons le résultat de nos expérimentations dans
la section 6. Enfin, nous concluons cet article par une synthèse et des perspectives.
Casanova
473
2. Problème du mariage stable
Nous étudions ici le problème des mariages stables, en anglais Stable Marriage
Problem, qui a été introduit par Gale et Shapley (1962). Ce problème s’énonce simplement. On considère n individus d’une communauté (e.g la gent féminine) et n
individus d’une autre communauté (e.g. la gent masculine). Chaque individu a des
penchants pour les individus de l’autre partition avec lesquels il souhaite être apparié.
Définition 1 (SM). — Un problème de mariage stable de taille n (avec n ≥ 1) est un
couple SM = hX, Yi avec |X| = |Y| = n, où:
– X = {x1 , . . . , xn } est un ensemble de n hommes, i.e. relations de préférence sur
Y, représentant les préférences des hommes sur l’ensemble des femmes.
– Y = {y1 , . . . , yn } est un ensemble de n femmes, i.e. relations de préférence sur X,
représentant les préférences des femmes sur l’ensemble des hommes.
On note y2 x1 y3 le fait que l’homme x1 préfère strictement la femme y2 à la
femme y3 . Dans cet article, on suppose que les relations de préférences sont des ordres
stricts, ce qui signifie que chaque individu est en mesure de choisir entre deux partenaires (il n’y a ni ex æquo, ni indifférence). On appelle problème de mariage stable
avec liste complète (SMC) un problème SM où toutes les préférences sont complètes
(tous les individus sont classés). Par opposition, dans un problème de mariage stable
incomplet (SMI), au moins l’une des listes de préférence est incomplète. Le fait qu’une
liste de préférences soit incomplète signifie que l’individu préfère rester seul plutôt
que d’être mal accompagné.
Résoudre un problème SM consiste à assortir ces communautés. On appelle appariement, en anglais matching, un ensemble de n mariages monogames et hétérosexuels.
Définition 2 (Appariement). — Un appariement M pour le problème SM = hX, Yi de
taille n est une application µ M : X ∪ Y → X ∪ Y ∪ {θ} 1 telle que:
– ∀x ∈ X, µ M (x) ∈ Y ∪ θ et ∀y ∈ Y, µ M (y) ∈ X ∪ θ
– ∀z ∈ X ∪ Y, si µ M (z) , θ alors µ M (µ M (z)) = z
µ M (z) représente le partenaire de z selon l’appariement M. Dans un appariement
complet, chaque individu est marié et l’application µ est involutive et donc bijective.
µ M (z) z µ M0 (z) signifie que z préfère (son partenaire dans) l’appariement M à (son
partenaire dans) M 0 . µ M (z) z µ M0 (z) si µ M (z) z µ M0 (z) ou µ M (z) = µ M0 (z). Dans
le cas d’un problème SMC, seul les appariements complets sont intéressants. À l’inverse, pour un problème SMI, certains appariements complets sont irrationnels car ils
consistent à marier un individu à un partenaire qui n’est pas dans sa liste de préférences.
1. θ dénote l’individu fantôme.
474
RIA. Volume 26 – no 5/2012
Un appariement est stable s’il n’existe pas de couple qui préférerait être ensemble
plutôt qu’avec leur partenaire actuel. En d’autres termes, il n’existe pas de relation
extra-congugale menaçant l’appariement. Ces relations prennent la forme de couples
hypothétiques bloquants :
Définition 3 (Stabilité). — Soient un problème SM = hX, Yi de taille n et M un
appariement pour SM. Un couple (xi , yi ) ∈ X × Y est bloquant si yi xi µ M (xi ) et
xi yi µ M (yi ). M est instable s’il existe un couple bloquant.
Un appariement stable est une solution admissible à un problème SMC. Dans le cas
d’un problème SMI, un appariement stable est admissible s’il est rationnel, c’est-à-dire
si chacun des individus est marié à un partenaire qui est dans sa liste de préférences.
Exemple 4. —
Soit les relations de préférence suivantes SM
=
h{x1 , x2 , x3 }, {y1 , y2 , y3 }i avec :
y2 x1 y1 x1 y3
x2 y1 x1 y1 x3
y3 x2 y2 x2 y1
x3 y2 x2 y2 x1
y1 x3 y3 x3 y2
x1 y3 x3 y3 x2
Pour ce SMC, l’appariement M (µ M (x1 ) = y2 , µ M (x2 ) = y1 , µ M (x3 ) = y3 ) est instable
car (x2 , y2 ) est un couple bloquant. À l’inverse, les trois appariements M1 , M2 et M3
sont stables :
– µ M1 (x1 ) = y1 , µ M1 (x2 ) = y2 , µ M1 (x3 ) = y3
– µ M2 (x3 ) = y1 , µ M2 (x1 ) = y2 , µ M2 (x2 ) = y3
– µ M3 (x2 ) = y1 , µ M3 (x3 ) = y2 , µ M3 (x1 ) = y3
L’algorithme de Gale-Shapley (GS) proposé dans (Gale, Shapley, 1962) est une
preuve constructive de l’existence d’une solution admissible pour n’importe quelle
instance de SM (complet ou non).
L’algorithme GS peut être décrit comme un cérémonial au cours duquel les femmes
attendent dans une salle et les hommes, qui sont à l’extérieur, rentrent à tour de rôle
dans un ordre arbitraire. Quand un homme entre, il se présente à la femme qu’il préfère. Si la femme est libre et qu’elle le considère comme acceptable (i.e. il est dans
sa liste de préférences), il devient son partenaire. Si elle a déjà un partenaire, il y a
conflit et elle choisit l’homme qu’elle préfère. L’élu reste et l’autre, rejeté, sort de la
pièce. Ce dernier se souvient de cet échec et reviendra plus tard pour se présenter à
la femme qui suit dans l’ordre de ses préférences. On s’arrête quand tous les hommes
qui ne sont pas libres sont désespérés (leur liste de préférences est vide).
Dans l’algorithme GS (cf. algorithme 1) tel que nous le présentons, les hommes
proposent et les femmes disposent. Une exécution consiste en une séquence de propositions des hommes envers les femmes. En d’autres termes, les hommes jouent le
rôle de proposant et les femmes jouent le rôle de répondant. On dit que GS est orienté
homme. Il peut être facilement adapté pour être orienté femme, en inversant leur rôle
respectif. Dans ce cas, les femmes proposent et les hommes disposent.
Casanova
475
Algorithme 1 . GS orienté homme
Entrée : un problème SM
Sortie : un appariement M
Tous les individus sont libres
tant que il existe un homme libre x qui ne soit pas désespéré faire
y ← la première femme de la liste de x
// x propose à y
x2 ← est le partenaire courant de y éventuellement θ
si y considère x comme acceptable alors
Marier x et y
// y dispose
si x2 n’est pas un fantôme (i.e. θ) alors
x2 ← libre
fin si
pour chaque successeur x3 de x dans la liste de y faire
Supprimer x3 de la liste de y
// y ne fait plus de concession
Supprimer y de la liste de x3
// y informe ceux concernés
fin pour
fin si
fin tant que
Exemple 5. — En considérant le SM de l’exemple 4, le résultat de l’algorithme GS
orienté homme (respectivement orienté femme) est l’appariement M2 (respectivement
M3 ). L’appariement M1 ne peut être atteint par aucune exécution de GS qu’il soit
orienté homme ou femme.
L’agentification de cette résolution est simple et directe. C’est l’objet de la méthode
DisEGS proposée par (Brito, Meseguer, 2005) qui consiste à faire négocier deux types
d’agents – les proposants et les disposants – pour faire émerger une solution admissible. Les propriétés respectives de DisEGS et d’autres approches sont discutées dans
la section 5 et la qualité de leur solution est comparée dans la section 6.
3. Évaluation sociale des appariements
Comme nous l’avons vu dans la section précédente, un problème de mariages peut
avoir plusieurs solutions stables. Pour les distinguer les unes des autres, nous considérons ici différentes métriques. Dans la section 3.1, nous rappelons quelques résultats
formels de la théorie des jeux qui soulignent que l’optimalité sociale permet de distinguer certaines solutions mais que cette métrique reste insuffisamment discriminante.
Dans la section 3.2, nous nous inspirons de la théorie du choix social pour proposer
nos propres métriques.
3.1. Optimalité sociale
Une fois qu’un appariement est établi, il est essentiel de déterminer à quel point cet
appariement est acceptable pour la société. Dans cette section, nous utilisons la théorie
476
RIA. Volume 26 – no 5/2012
des jeux pour évaluer les solutions admissibles à un problème SM (Roth, Oliveira Sotomayor, 1990). Pour la clarté, nous nous restreignons dans la suite de cet article au
problème avec liste complète (SMC). Nous évaluons alors les solutions admissibles,
i.e. celles qui sont stables.
Un appariement stable est le résultat d’un jeu entre deux communautés. Il peut être
évalué du point de vue d’une communauté ou de l’autre.
Définition 6 (Préférence communautaire). — Soit un problème SM = hX, Yi de taille
n. Soient M et M 0 deux appariements stables pour SM et E ⊆ (X ∪ Y). M paretodomine M 0 sur E ssi ∀z ∈ E µ M (z) z µ M0 (z) et ∃z ∈ E tq µ M (z) z µ M0 (z). Un
appariement est pareto-optimal si c’est un appariement stable qui n’est pas pareto
dominé sur X ∪ Y. Un appariement est pareto mâle-optimal (respectivement pareto
femelle-optimal) si c’est un appariement stable qui n’est pas pareto-dominé sur X
(respectivement Y).
Donald Knuth a démontré dans (Knuth, 1971) que l’exécution de l’algorithme GS
orienté homme aboutit à une solution – un appariement stable – qui est mâle-optimale
et que cette solution est une des pires du point de vue des femmes.
Théorème 7 (Knuth, 1971, Conflit global). — Soit un problème SM.
– Il y a toujours un appariement qui est mâle-optimal, i.e. le résultat de l’algorithme GS orienté homme.
– Il y a toujours un appariement qui est femelle-optimal, i.e. le résultat de l’algorithme GS orienté femme.
– Tous les appariements qui sont mâle-optimaux sont pareto-dominés sur les
femmes par les autres appariements stables.
Comme l’espace des versions bien connu en apprentissage automatique (Mitchell,
1997), l’espace des solutions stables est un treillis. L’espace que l’on envisage ici
ne s’appuie pas sur une relation de généralisation mais sur la relation de paretodominance (e.g. sur les femmes) et la frontière supérieure est constituée des mâleoptimaux alors que la frontière inférieure est l’ensemble des solutions femelle-optimales. Chacune des solutions frontières peut être atteinte par l’algorithme GS en modifiant l’ordre d’apparition des proposants. Toutes les autres solutions, hors des frontières, ne peuvent être atteintes par l’algorithme GS mais par un algorithme centralisé
qui passe d’un appariement stable à un autre appariement stable en dégradant la satisfaction d’une communauté ou de l’autre communauté.
Dans une situation stable, si un individu souhaite divorcer pour un partenaire qu’il
préfère alors ce coup s’effectue au détriment de son partenaire courant. Ces dilemmes
sont capturés par le théorème suivant.
Théorème 8 (Knuth, 1971, Conflit local). — Soient M et M 0 deux appariements
stables pour un problème SM. Si µ M (x) = y et µ M0 (x) , y , alors
– soit µ M0 (x) x µ M (x) et µ M (y) y µ M0 (y);
– soit µ M (x) x µ M0 (x) et µ M0 (y) y µ M (y).
Casanova
477
La stabilité est une condition suffisante à la pareto-optimalité mais ce n’est pas une
condition nécessaire.
Théorème 9 (Roth, Oliveira Sotomayor, 1990, Pareto optimalité). — Tout appariement stable est un optimum de Pareto.
Preuve 10 (Pareto optimalité). — Par l’absurde, supposons qu’un appariement stable
M n’est pas pareto-optimal. Alors, il existe un appariement M 0 qui pareto-domine M
sur X ∪ Y. En conséquence,
∃z ∈ X ∪ Y t.q. µ M0 (z) z µ M (z)
(1)
∀z0 , z, µ M0 (z0 ) z0 µ M (z0 )
(2)
et
Notons h = µ M (z) et h0 = µ M0 (z). Avec 1, on a µ M0 (z) z µ M (z) et on peut déduire que
h0 z h. Comme h0 , z, grâce à l’équation 2, µ M0 (h0 ) h0 µ M (h0 ), donc z h0 µ M (h0 ).
Comme l’ordre considéré est strict et complet et que µ M (h0 ) , z, on a z h0 µ M (h0 ). M
n’est pas stable car (z, h0 ) est bloquant.
On peut noter qu’un appariement pareto-optimal n’est pas nécessairement stable.
Théorème 11. — Tout appariement pareto-optimal n’est pas stable.
Preuve 12. — Soit le SM = h{x1 , x2 }, {y1 , y2 }i avec y2 x1 y1 , y2 x2 y1 , x2 y1 x1 et
x2 y2 x1 . Considérons l’appariement M tel que µ M (x1 ) = y2 et µ M (x2 ) = y1 . M est
pareto-optimal mais cet assignement n’est pas stable car le couple (x2 , y2 ) est bloquant.
Exemple 13. — En considérant le SM de l’exemple 4, l’appariement M2 (respectivement M3 ) est mâle optimal (respectivement femelle optimal) car les hommes (respectivement femmes) sont mariés avec leur partenaire préféré. L’appariement M1 , où
tous les individus sont mariés avec leur second partenaire préféré, est un optimum de
pareto comme M2 et M3 .
En résumé, l’optimalité au sens de Pareto permet de distinguer parmi les solutions
stables lesquelles sont meilleures du point de vue d’une communauté ou d’une autre,
mais elle ne permet pas de distinguer lesquelles sont les meilleures du point de vue de
la société globale.
3.2. Bien-être social
Afin d’évaluer la qualité d’une solution du point de vue collectif, la théorie du
choix social (Moulin, 2003) propose d’autres outils que la théorie des jeux. Cette
évaluation repose sur une mesure individuelle de la satisfaction des individus, qui est
ensuite agrégée afin d’estimer la satisfaction de toute (ou partie de) la société.
Pour le problème SM, chaque individu (quelle que soit sa communauté) évalue sa
satisfaction en fonction de ses préférences via son regret qui est : 0 s’il est marié avec
478
RIA. Volume 26 – no 5/2012
le premier individu de sa liste; 1 s’il est marié avec le deuxième individu de sa liste,
etc. Moins un individu a de regret, plus sa satisfaction est grande.
Définition 14 (Satisfaction individuelle). — Soient un problème SM = hX, Yi de taille
n et un individu z. Considérons l’appariement M. Si le rang de µ M (z) dans z est k
(avec 0 ≤ k < n), alors le regret de z dans l’appariement M (noté rz (µ M (z))) est k. La
fonction d’utilité de l’individu z est la fonction uz : X ∪ Y → [0, 1] définie telle que :
( (n−1)−k
si µ M (z) , θ
n−1
uz (µ M (z)) =
(3)
0
sinon
(Moulin, 2003) propose de nombreuses fonctions pour agréger les utilités des individus, comme par exemple le bien-être utilitaire. Nous adaptons cette mesure au
problème SM afin d’évaluer le point de vue global, et nous introduisons la mesure
de bien-être équitable pour évaluer les disparités entre communautés et le bien-être
conjugal pour évaluer les disparités entre les partenaires d’un même couple.
Définition 15 (Satisfaction collective). — Soit un problème SM de taille n. Considérons un appariement M.
– Le bien-être utilitaire considère le bien-être de toute la société :
1 X
uz (µ M (z))
swu (X ∪ Y) =
2n z∈X∪Y
(4)
– Le bien-être masculin considère la satisfaction des hommes :
swu (X) =
1X
u x (µ M (x))
n x∈X
(5)
– Le bien-être féminin considère la satisfaction des femmes :
swu (Y) =
1X
uy (µ M (y))
n y∈Y
(6)
– Le bien-être équitable considère l’équité entre les hommes et les femmes :
X
1 X
swe (X ∪ Y) = 1 − |
u x (µ M (x)) −
uy (µ M (y))|
n x∈X
y∈Y
(7)
– Le bien-être conjugal considère l’équité dans les mariages :
swc (X ∪ Y) = 1 −
1 X
|u x (µ M (x)) − uµM (x) (x)|
n (x,µ (x))∈M
(8)
M
Les notions de bien-être présentées ici ont été normalisées (entre 0 et 1). Pour le
bien-être utilitaire, masculin et féminin, plus le bien-être est grand, plus la solution est
Casanova
479
optimale du point de vue de la communauté envisagée. Pour le bien-être équitable et
conjugal, plus le bien-être est grand, plus la solution est probe. On peut noter que le
bien-être conjugal est un raffinement du bien-être équitable qui s’inspire du principe
sous-jacent à l’algorithme Zig-Zag (Zavidovique et al., 2005) discuté dans la section 5.
Nous avons choisi d’envisager l’équité entre les communautés ainsi que l’équité au
sein des couples plutôt le bien-être égalitaire qui considère le bien-être de l’agent le
plus insatisfait car cette notion est indépendante de la communauté. Pour une même
instance de problème SM, l’agent le moins satisfait par une solution admissible peutêtre un homme et l’agent le moins satisfait par une autre solution admissible peut-être
une femme. La comparaison des solutions admissibles à l’aide de cette métrique n’est
donc ni simple ni directe.
Exemple 16. — Si nous considérons de nouveau l’exemple 4, les bien-être pour les
différents appariements stables sont les suivants :
Bien-être
swu (X ∪ Y)
swu (X)
swu (Y)
swe (X ∪ Y)
swc (X ∪ Y)
M1
.5
.5
.5
1
1
M2
.5
1
0
0
0
M3
.5
0
1
0
0
L’appariement M1 , qui ne peut pas être atteint par l’algorithme GS, est la solution la
plus équitable et la plus juste pour les couples.
4. Méthode Casanova
Contrairement à GS qui décrit un cérémonial, la méthode que nous proposons,
Casanova, décrit le comportement d’agents négociant. Dans GS, chaque communauté se voit attribuer un rôle, proposant ou disposant, alors que dans Casanova, les
agents jouent simultanément le rôle de disposant et de proposant dans une multitude
de négociations bilatérales. Casanova réalise alors une stratégie de concession minimale (Rosenschein, Zlotkin, 1994 ; Morge, Mancarella, 2010), basée sur le regret des
agents, pour permettre aux agents de faire émerger un appariement stable plus équitable que la solution proposée par GS. Selon cette stratégie, les agents se proposent
à leurs partenaires préférés. En cas d’échec, un agent concède, ce qui se traduit par
l’abandon de ses exigences vis-à-vis des partenaires potentiels. Ainsi, au début, un
agent envoie une proposition à son unique partenaire préféré, et si ce dernier refuse
l’agent concède et donc envoie une nouvelle proposition aux deux partenaires qu’il
préfère, etc.
4.1. Comportement des agents
Dans Casanova, chaque individu est représenté par un agent dont l’état interne est
défini comme suit.
480
RIA. Volume 26 – no 5/2012
Définition 17. — Soient SM = hX, Yi un problème de taille n et un agent a ∈ A
représentant l’individu z ∈ X ∪ Y. À chaque instant, l’agent a est représenté par un
tuple hσ, π, κ, µ, λ, ω, αi où :
– σ ∈ {>, ⊥} est le statut marital (> si marié avec un autre agent, ⊥ sinon) ;
– π est la liste de préférences de l’agent, ordonnée grâce à la relation z (cf. Définition 1) ;
– κ ∈ [0, n[ est le niveau de concession ou niveau de regret courant ;
– µ ∈ X ∪ Y ∪ {θ} est le partenaire courant ;
– λ ∈ X ∪ Y ∪ {θ} est l’amant courant ;
– ω ∈ [0, n] est un compteur de messages sans réponse ;
– α est la liste des acceptants.
Par souci de concision, on considère z ≡ a et X ∪ Y ≡ A. On définit le niveau
de concession comme la position maximale dans la liste de préférences que l’agent
considère comme acceptable. On note qu’un agent n’est pas forcément marié avec son
partenaire courant µ : il peut être fiancé (σ = ⊥ et µ , θ). De plus, un amant λ est
un agent qui fait une proposition acceptable (ra (λ) < κ) à un agent a déjà marié ayant
un niveau de concession κ. Le compteur ω sert à déterminer si l’agent attend encore
des réponses aux propositions qu’il a lancées. Il est décrémenté automatiquement à
la réception d’un accept ou d’un reject à la proposition en cours. La liste des
acceptants α correspond à l’ensemble des agents ayant accepté une des propositions
de l’agent. Elle est automatiquement mise à jour à la réception d’un message accept
à la proposition en cours.
À l’initalisation et pour tous les agents, σ = ⊥, κ = 1, µ = θ, λ = θ, ω = 0, α = [].
Les préférences π varient d’un agent à l’autre.
Nous pouvons représenter le comportement des agents grâce à un automate fini
déterministe composé de 5 états : libre (free), hésitant (hesitating), fiancé (engaged),
marié fidèle (faithful), et marié infidèle (unfaithful). Chacun de ces états dépend des
valeurs de certains attributs de l’agent (µ, λ, σ et ω), comme présenté ci-dessous :
état
free
hesitating
engaged
faithful
unfaithful
µ
θ
a∈A
a∈A
a∈A
a∈A
λ
θ
θ
θ
θ
a0 ∈ A
σ
⊥
⊥
⊥
>
>
ω
>0
>0
=0
=0
=0
Les transitions entre états et leurs conditions sont représentées dans la figure 1.
Les actions consécutives aux transitions sont exprimées dans le tableau 1, pour plus
de lisibilité 2 .
2. Pour simplifier, les mises à jours automatiques de ω et α à chaque réception de messages accept ou
reject n’apparaissent pas dans le tableau 1.
Casanova
481
Un agent peut envoyer les messages suivants :
– propose pour faire une proposition à un autre agent ;
– accept (resp. reject) pour répondre positivement (resp. négativement) à une
proposition émanant d’un autre agent ;
– confirm (resp. withdraw) pour confirmer (resp. infirmer) le mariage, suite à
une acceptation ;
– divorce pour briser un mariage.
Tableau 1. Actions consécutives aux transitions d’états
origine
destination
free
free
condition
reject & ω=0 & all are reject
free
free
free
free
hesitating
faithful
hesitating
hesitating
hesitating
engaged
hesitating
faithful
engaged
engaged
engaged
free
(accept or reject) & ω , 0
propose & level(y)<κ
(accept or reject) & best(α), θ &
ω=0
propose
(accept or reject) & ω=0 & µ x
best(α)
(accept or reject) & ω=0 &
best(α) x µ
propose
withdraw & y=µ
engaged
faithful
faithful
faithful
faithful
free
confirm & µ=y
propose & µ x y
divorce
faithful
unfaithful
unfaithful
unfaithful
unfaithful
unfaithful
engaged
faithful
propose & y x µ
propose
divorce
confirm & λ=y
action
κ++; send(propose) to all m peers at concession
level κ; α ← []; ω ← m;
∅
µ←y
µ
← best(α); send(confirm) to µ;
send(withdraw) to every z ∈ α \ {µ}; σ ← >
send(reject) to y
send(accept) to µ; send(withdraw) to every z ∈
α
send(reject) to µ; µ ← best(α); send(confirm)
to µ; send(withdraw) to every z ∈ α\{µ}; σ ← >
send(reject) to y
σ ← ⊥; µ ← θ; κ++; send(propose) to all m
peers at concession level κ; α ← []; ω ← m
σ←>
send(reject) to y
σ ← ⊥; µ ← θ; κ++; send(propose) to all m
pairs at concession level κ; α ← []; ω ← m
λ ← y; send(accept) to y
send(reject) to y
µ ← λ; λ ← θ; σ ← ⊥
send(divorce) to µ; µ ← λ; λ ← θ
4.2. Automate
La méthode Casanova correspond à l’exécution en parallèle des automates finis déterministes correspondants à la figure 1, pour chacun des agents des deux communautés. Tous les agents ont donc le même comportement, mais des préférences différentes.
Chaque agent mène trois activités de front : (i) la proposition ; (ii) la disposition ; et
(iii) la remise en question.
Proposition. Au début de la résolution, chaque agent est libre (free). L’agent a
lance des propositions aux agents qu’il considère comme acceptables (b ∈ π, t.q.
ra (b) < κ). Lorsqu’il a reçu toutes les réponses (ω = 0) et au moins une acceptation
avant toute autre proposition, il envoie un message de confirmation au meilleur et il
devient marié (faithful). En l’absence d’acceptation parmi toutes les réponses et en
l’absence d’autre proposition, l’agent augmente son niveau de concession κ. Il recommence alors une phase de proposition avec un niveau de concession supérieur. Dès
qu’un agent reçoit une proposition, il passe en phase de disposition (hesitating). Par
contre, si à l’issue de cette activité de proposition, il est marié (il a reçu toutes les ré-
482
RIA. Volume 26 – no 5/2012
propose
divorce
engaged
unfaithful
confirm
withdraw
&y=µ
propose
(accept or reject)
&y=µ
&ω=0
& best=µ
(accept or reject)
& ω=0 &
best(α)≺ x µ
hesitating
propose &
level(y)<κ
faithful
propose
& y ≺x µ
terminate
•
divorce
propose
& µ ≺x y
(accept or reject)
&ω,0
•
propose
confirm
& λ=y
free
(accept or reject)
& best(α), θ
& ω=0
reject & ω=0
& all are reject
Figure 1. Comportement des agents représenté comme un automate fini déterministe
ponses à sa proposition et aucune autre proposition), alors il passe en phase de remise
en question (voir plus bas).
Disposition. Lorsqu’un agent reçoit une proposition alors qu’il est libre et donc en
attente de réponses, il va hésiter (hesitating) entre cette proposition et les éventuelles
réponses positives à celle qu’il a émise. Il attend donc toutes les réponses des agents
auxquels il a fait une proposition. Lorsqu’il a reçu toutes les réponses (ω = 0) il va :
(i) soit accepter la proposition si elle est préférable au meilleur des acceptants - dans
ce cas l’agent est fiancé (engaged) et attend une confirmation pour se marier ; (ii) soit
confirmer au meilleur des acceptants et l’agent devient alors marié. Dans tous les cas,
les autres agents reçoivent des réponses négatives (reject ou withdraw). À la fin
de cette phase l’agent est : (i) soit marié et va donc pouvoir se remettre en question
(voir plus bas) ; (ii) soit libre s’il a accepté la proposition mais que cette dernière est
annulée par un withdraw et l’agent augmente donc son niveau de concession pour
recommencer le processus de proposition.
Remise en question. Ce n’est pas parce qu’un agent est marié, qu’il va le rester
tout au long de la résolution. En effet, il peut recevoir des propositions plus intéressantes que son partenaire actuel. Dans ce cas, l’agent continue à être marié mais fait
une « infidélité » (unfaithful) en acceptant une proposition. Si cette dernière aboutit sur
une confirmation, l’agent divorce de son partenaire actuel (µ) et se marie avec le proposant (l’amant λ), sinon l’agent reste fidèle. Lorsqu’un agent reçoit un message de
divorce, il devient : (i) soit libre s’il n’a pas d’amant, et donc il recommence une phase
Casanova
483
de proposition ; (ii) soit fiancé avec son amant et donc en attente d’une confirmation
dans une phase de disposition.
Arrêt. La résolution se termine lorsque tous les agents sont mariés, qu’ils soient
fidèles ou non.
Figure 2. Trace d’exécution de Casanova du point de vue de l’agent y3
Exemple 18. — Considérons l’exemple 4 du point de vue de y3 . Les messages envoyés
ou reçus par y3 sont représentés dans la figure 2. Pour rappel, les préférences de y3 sont
x1 y3 x3 y3 x2 . Initialement, y3 est free et son niveau de concession κ = 0. Ainsi, le
seul partenaire acceptable est x1 . Dans notre exemple, les négociations conduisent à
l’appariement M1 t.q. µ M1 (x1 ) = y1 , µ M1 (x2 ) = y2 , µ M1 (x3 ) = y3 avec swe (X ∪ Y) = 1.
Tout d’abord, y3 reçoit une proposition d’un partenaire non acceptable, x2 (message 1).
Ainsi, y3 rejette cette proposition (message 2). Indépendamment de cette proposition,
y3 fait une proposition à son partenaire préféré, x1 (message 3). Entre temps, y3 reçoit
une deuxième série de propositions non acceptables de x2 et de x3 (messages 4 et
6), qu’elle rejette immédiatement (messages 5 et 7). Malheureusement, la proposition
de y3 est rejetée par x1 . Par conséquent, elle concède (κ ← 2) et elle avance dans
sa liste de préférences. y3 envoie une proposition à x1 (message 9) et x3 (message
10), qui sont toutes deux rejetées (messages 11 et 12). Par conséquent, y3 concède à
nouveau et envoie une proposition à ses trois partenaires acceptables, x1 (message 13),
x3 (message 14) et x2 (message 15). x2 et x3 acceptent (messages 16 et 17) et ils se
484
RIA. Volume 26 – no 5/2012
considèrent fiancés en attente de confirmation. x1 rejette la proposition (message 18).
y3 choisit le meilleur acceptant (x3 ), confirme le mariage (message 19), et annule sa
proposition à x2 (message 20).
5. Travaux connexes
Dans cette section, nous comparons Casanova avec les méthodes existantes en
fonction des caractéristiques exhibées par notre méthode : la décentralisation (cf. section 5.1), la privacité (cf. section 5.2) et l’équité (cf. section 5.3). Comme résumé dans
le tableau 2, notre analyse de l’état de l’art conclut que Casanova est la seule méthode
de résolution qui, à notre connaissance, dispose simultanément de ces trois propriétés.
Tableau 2. Propriétés des méthodes de résolution du S M
Méthode
GS (Gale, Shapley, 1962)
DisEGS (Brito, Meseguer, 2005)
DisFC (Brito, Meseguer, 2005 ; 2007)
Zig-Zag (Zavidovique et al., 2005)
SML2 (Gelain et al., 2010)
Casanova (Everaere et al., 2011)
Décentralisé
7
3
3
7
7
3
Privacité
7
3
3
7
7
3
Équité
7
7
7
3
3
3
5.1. Décentralisation
Parmi les méthodes existantes, nous distinguons les algorithmes centralisés où
une entité principale collecte les informations pour effectuer la totalité du calcul et les
méthodes décentralisées où les informations et le calcul sont (au moins partiellement)
distribués.
L’algorithme séminal de Gale-Shapley (GS) proposé dans (Gale, Shapley, 1962)
se résume au cérémonial décrit dans la section 2. Selon cet algorithme, une entité
centrale joue le rôle de marieuse en fonction des préférences des individus dont elle a
connaissance. L’algorithme GS est clairement une méthode centralisée.
La méthode DisEGS (Brito, Meseguer, 2005) évoquée dans la section 2 résulte
de l’agentification de l’algorithme GS. Les échanges de propositions et d’acceptation
permettent d’atteindre un appariement. Les préférences et le calcul de l’appariement
sont distribués. Cette méthode est donc décentralisée.
L’algorithme DisFC (Brito, Meseguer, 2006 ; 2007) est une adaptation de l’algorithme ABT (Yokoo et al., 1998). Comme ABT, l’algorithme DisFC est une méthode
distribuée de résolution de problèmes de satisfaction de contraintes – Constraint Solving Problem (CSP). L’algorithme DisFC résout un CSP qui est la traduction d’un problème SM. Nous considérons ici que l’algorithme DisFC est une méthode de résolution décentralisée comme cela est communément admis pour ABT. Toutefois, on peut
remarquer que cette méthode nécessite un ordonnancement entre les agents. Ainsi,
Casanova
485
certains agents capturent une grande partie de la complexité du problème et ceux-ci
doivent résoudre une large partie (voire l’intégralité) du problème. Comme discuté
dans (Glize, Picard, 2011), cette asymétrie peut impliquer des points de centralisation.
L’algorithme Zig-Zag (Zavidovique et al., 2005) consiste à parcourir une table
dont les lignes (respectivement les colonnes) représentent les ordres de préférences
des hommes (respectivement des femmes). Comme cet algorithme s’appuie sur cette
table des mariages qui nécessite la connaissance complète du problème, cette méthode
est centralisée. À notre connaissance, cette approche ne peut pas être distribuée.
L’algorithme SML2 (Gelain et al., 2010) est un algorithme d’optimisation par recherche locale qui vise à minimiser le nombre de mariages non stables. Cet algorithme
consiste, à partir d’un appariement aléatoire, à améliorer la stabilité de l’appariement
en supprimant des mariages non stables. De par la notion de voisinage utilisée, cette
méthode est centralisée.
5.2. Privacité
Le respect de la vie privée est désormais considéré comme une caractéristique
cruciale que doivent exhiber les systèmes informatiques. Dans le cas particulier des
mariage stables, nous considérons que les préférences des individus, le statut marital
et leur partenaire sont des informations sensibles de la sphère privée. Selon nous, une
méthode de résolution garantit la privacité si ces informations ne sont pas divulguées
explicitement lors d’échanges avec tout ou partie du système. Notre définition omet
deux aspects de la privacité :
– la délégation de confiance entre les agents. Nous n’envisageons pas que des
agents puissent publier des informations sur d’autres agents (par exemple, un agent
publie la liste des agents qui l’ont contacté) ;
– la traçabilité des échanges : nous ne considérons pas que les agents puissent
écouter les échanges entre les autres agents pour en inférer certaines connaissances
(par exemple, déduire une liste de préférences à partir d’une trace des échanges).
Par définition, les méthodes de résolution centralisées (e.g. GS, Zig-Zag et SML2) ne
préservent pas la privacité. À l’inverse, les méthodes de résolution comme DisEGS et
Casanova ne nécessitent pas que les agents révèlent explicitement leurs préférences,
leur statut marital ou l’identité de leur partenaire. Ces méthodes respectent la privacité. En ce qui concerne l’algorithme DisFC, les agents échangent une partie de ces
informations. Toutefois, ces données échangées sont cryptées dans la version PKC, ce
qui garantit ainsi la privacité.
5.3. Équité
Nous qualifions d’équitable les méthodes de résolution du problème SM qui optimisent la justice entre les communautés d’agents. Concrètement, ces méthodes tentent
de réduire l’écart entre la satisfaction des hommes et celle des femmes.
486
RIA. Volume 26 – no 5/2012
Comme nous l’avons souligné dans la section 2, l’algorithme GS et sa version
décentralisée DisEGS favorisent une communauté au détriment d’une autre. Si les
hommes proposent et les femmes disposent, l’appariement résultant est mâle-optimal.
Inversement, si les femmes proposent et les hommes disposent, l’appariement résultant est femelle-optimal (cf. théorème 7). L’inéquité des solutions s’explique par le fait
que ces méthodes de résolution sont asymétriques. Le traitement des individus dépend
de leur communauté d’appartenance.
L’algorithme DisFC s’appuie sur un ordre arbitraire entre hommes et femmes.
Cette méthode traite différemment les hommes et les femmes. (Brito, Meseguer, 2005 ;
2007) ne proposent pas de mécanisme pour garantir l’équité comme la possibilité d’un
ordonnancement aléatoire des agents, par exemple.
La méthode Casanova consiste en un seul et unique comportement d’agent indépendamment de leur communauté d’appartenance. Ainsi, son objectif est d’atteindre
une solution équitable. De même, l’algorithme SML2 traite les individus indépendamment de sa communauté d’appartenance. Il vise également l’équité de la solution. On
peut toutefois noter que l’appariement obtenu n’est pas nécessairement stable.
L’algorithme Zig-Zag parcours la table des mariages où chaque case (p, q) contient
une paire (m, w) telle que w est le p-ième choix de m, et m est le q-ième choix de w.
Le parcours de la table s’effectue sur la diagonale pour y choisir si possible un couple
et en s’en écartant au minimum sinon. Intuitivement, ce cheminement vise à favoriser
la justice au sein des couples, mais, comme SML2, il ne garantit pas que le résultat
soit stable.
Afin d’évaluer précisément la justice des solutions, nous avons introduit dans la
définition 15 deux métriques : le bien-être équitable (cf. équation 7) et le bien-être
conjugal (cf. équation 8). Nos expérimentations, présentées dans la section suivante,
comparent les algorithmes mentionnés ici selon ces métriques.
6. Expérimentation et évaluation
Dans cette section nous présentons le résultat de nos expérimentations qui permettent de comparer notre méthode avec celles existantes. Casanova a fait l’objet de
deux implémentations.
6.1. Conditions expérimentales
Dans un premier temps, nous avons utilisé la plateforme multi-agent Jason (Bordini
et al., 2007). Jason est une version étendue du langage AgentSpeak (Rao, 1996) qui
implémente la sémantique opérationnelle de ce langage. Jason permet de prototyper rapidement le comportement des agents. Cette implémentation est une preuve de
concept en faveur de la décentralisation de notre approche (Everaere et al., 2011).
Notre résolution ainsi implémentée est distribuable dans un réseau grâce à une infrastructure Jade, par exemple. Pour ce faire, nous avons implémenté un processus
Casanova
487
distribué asynchrone inspiré de (Dijkstra, Scholten, 1980) qui permet de stopper les
négociations lorsqu’une solution stable est atteinte. Tous les agents sont placés dans un
graphe orienté constitué d’un unique circuit et ils échangent des jetons de terminaison.
Dans un second temps, nous avons entièrement réimplémenté Casanova en Java.
Cette version permet de comparer notre approche aux algorithmes existants, qu’ils
soient centralisés ou décentralisés, à l’aide du même langage de programmation. Le
protocole d’expérimentation que nous avons suivi est le suivant. Nous avons généré
de manière (pseudo-)aléatoire des instances de problèmes SM de tailles comprises
entre n = 2 et n = 100. Nous avons considéré 20 instances différentes pour chaque
n. Ces instances ont été résolues à l’aide des méthodes évoquées dans la section
précédente : Gale-Shapley (Gale, Shapley, 1962), DisEGS (Brito, Meseguer, 2005),
Zig-Zag (Zavidovique et al., 2005), SML2 (Gelain et al., 2010) et bien-sûr Casanova (Everaere et al., 2011). Nous présentons ici pour chacune des métriques, la
moyenne des résultats obtenus par chacun des algorithmes.
6.2. Bien-être masculin/féminin
La figure 3 représente le bien-être masculin (cf. équation 5 de la définition 15) et
le bien-être féminin (cf. équation 6 de la définition 15). Ces métriques confirment que
l’algorithme de Gale-Shapley orienté homme favorise les hommes au détriment des
femmes alors que Casanova obtient des résultats similaires aux méthodes SML2 et
Zig-Zag.
En complément, la figure 4 représente pour chacune des instances du problème
(20 instances pour des tailles allant de 2 à 100) l’évaluation multi-objectif de la solution pour les bien-être masculin et féminin (bien-être masculin en abscisse et bien-être
féminin en ordonnée). Cette figure permet de visualiser quelles régions du front de
Pareto sont explorées par chacune des méthodes. La région explorée par GS est excentrée par rapport à la diagonale. Comme dit précédemment, cette méthode favorise
une communauté plus qu’une autre. On voit également sur ces nuages de points que
les solutions explorées par les algorithmes Casanova et ZZ occupent des régions plus
centrales que les deux autres (proches de la diagonale), ce qui suggère que les solutions sont plus équitables.
6.3. Bien-être équitable/conjugal
La figure 5 représente le bien-être équitable (cf. équation 7 de la définition 15) et le
bien-être conjugal (cf. équation 8 de la définition 15). Pour ces deux métriques, Casanova se révèle aussi performant que Zig-Zag et légèrement plus performant que SML2.
Pour ces trois algorithmes, le bien-être équitable comme le bien-être conjugal des
solutions obtenues sont meilleurs que pour les solutions obtenues par GS qui favorise
une communauté au détriment de l’autre communauté. Nos expériences confirment
donc que Casanova fait émerger des solutions équitables.
488
RIA. Volume 26 – no 5/2012
1
Bien−être masculin
0.95
0.9
0.85
0.8
0.75
0.7
Casanova
Gale−Shapley
Zig Zag
SML
0.65
0.6
10
20
30
40 50 60 70
Taille du problème
80
90 100
1
Bien−être féminin
0.95
0.9
0.85
0.8
0.75
0.7
Casanova
Gale−Shapley
Zig Zag
SML
0.65
0.6
10
20
30
40 50 60 70
Taille du problème
80
90 100
Figure 3. Évaluation du bien-être masculin (en haut) et du bien-être féminin (en bas)
6.4. Bien-être utilitaire
La figure 6 représente le bien-être utilitaire (cf. équation 4 de la définition 15).
Pour cette métrique, tous les algorithmes, en particulier Casanova, sont meilleurs que
GS. Nos expériences montrent donc que Casanova améliore, au même titre que les solutions centralisées, la satisfaction globale de la société. En effet, les solutions stables
optimales ne sont pas nécessairement celles explorées par GS, c’est-à-dire parmi les
solutions mâle-optimales ou femelle-optimales.
6.5. Nombre de paires bloquantes
La figure 7 représente le nombre moyen de paires bloquantes, i.e. de relations
extra-conjugales, menaçant l’appariement (cf. définition 3), dans les solutions propo-
Casanova
0
Casanova
Bien−être féminin
Bien−être féminin
0
0.2
0.4
0.6
0.8
1
Gale−Shapley
0.2
0.4
0.6
0.8
1
1
0
0.8
0.6
0.4
0.2
Bien−être masculin
0
1
0
Zig Zag
Bien−être féminin
Bien−être féminin
489
0.2
0.4
0.6
0.8
1
0.8
0.6
0.4
0.2
Bien−être masculin
0
SML
0.2
0.4
0.6
0.8
1
1
0.8
0.6
0.4
0.2
Bien−être masculin
0
1
0.8
0.6
0.4
0.2
Bien−être masculin
0
Figure 4. Front de Pareto exploré par les différentes méthodes
sées par chacun des algorithmes. SML2 est une méthode d’optimisation par recherche
locale qui cherche à minimiser le nombre de paires bloquantes. SML2 est paramétré
par une probabilité de marche aléatoire (p = 0, 1 dans nos expériences) et un nombre
maximum de pas (ici, s = 300). SML2 ne garantit pas la stabilité de la solution et
nécessite un paramétrage fin, ce qui explique son décrochage pour des tailles d’instances supérieures à 70. La méthode Zig-Zag produit des solutions dites quasi stables.
Toutes les autres méthodes produisent des solutions stables. On remarque que, parmi
les méthodes équitables, Casanova est la seule qui aboutit à des résultats stables.
6.6. Nombre de messages
La figure 8 représente le nombre de messages échangés. Cette métrique permet
d’évaluer si le système est réellement distribuable sans impact sur le temps de réponse ; notamment en vérifiant si le nombre de messages augmente au plus linéairement avec la taille du problème. Selon cette métrique, il apparaît que Casanova est
bien moins performant que DisEGS. C’est le prix de l’équité et de l’optimalité des solutions obtenues. D’après les mesures effectuées dans (Brito, Meseguer, 2006), DisFC
produit environ 50 000 messages pour des instances de taille n = 10 ce qui est bien
supérieur aux 470 messages générés par Casanova pour des instances de même taille.
Finalement, la complexité communicationnelle de Casanova semble admissible.
490
RIA. Volume 26 – no 5/2012
1
Bien−être équitable
0.95
0.9
0.85
0.8
0.75
0.7
Casanova
Gale−Shapley
Zig Zag
SML
0.65
0.6
10
20
30
40 50 60 70
Taille du problème
80
90 100
1
Bien−être conjugal
0.95
0.9
0.85
0.8
0.75
0.7
Casanova
Gale−Shapley
Zig Zag
SML
0.65
0.6
10
20
30
40 50 60 70
Taille du problème
80
90 100
Figure 5. Évaluation du bien-être équitable (en haut)
et du bien-être conjugal (en bas)
6.7. Temps d’exécution
La figure 8 représente le temps d’exécution des différentes méthodes de résolution.
Cette métrique permet d’évaluer si ces méthodes passent l’échelle ; notamment en vérifiant si le temps de réponse augmente au plus linéairement avec la taille du problème.
Selon cette métrique, il apparaît que Casanova est bien moins performant que GaleShapley. C’est le prix de l’équité et de l’optimalité des solutions obtenues. Toutefois,
si on compare Casanova aux autres méthodes de résolution qui prônent l’équité, Casanova se révèle beaucoup plus performant que SML2 et un peu moins performant
que Zig-Zag qui retournent toutes deux des solutions qui ne sont pas nécessairement
stables.
Casanova
491
1
Bien−être utilitaire
0.95
0.9
0.85
0.8
0.75
0.7
Casanova
Gale−Shapley
Zig Zag
SML
0.65
0.6
10
20
30
40 50 60 70
Taille du problème
80
90 100
Figure 6. Evaluation du bien-être utilitaire
Nombre de paires bloquantes
50
45
40
Casanova
Gale−Shapley
Zig Zag
SML
35
30
25
20
15
10
5
0
10
20
30
40 50 60 70
Taille du problème
80
90
100
Figure 7. Évaluation du nombre de paires bloquantes
7. Conclusion
Dans cet article, nous avons adopté une approche centrée individu pour la résolution du problème des mariages stables. Selon notre méthode, les agents interagissent
dans une multitude de négociations bilatérales. Notre comportement d’agent Casanova
consiste à mettre en œuvre une stratégie de concession minimale. Ainsi, au début, les
agents envoient une proposition à leur partenaire préféré, et s’il refuse ils concèdent
et donc envoient une nouvelle proposition aux deux agents qu’ils préfèrent, etc. De
plus, les agents mariés peuvent être amenés à divorcer si l’un des époux reçoit une
proposition préférable.
492
RIA. Volume 26 – no 5/2012
Nombre de messages
100000
10000
1000
100
10
Casanova
Gale−Shapley (DisEGS version)
1
10
20
30 40 50 60 70
Taille du problème
80
90 100
Figure 8. Evaluation du nombre de messages
100000
Time (ms)
10000
Casanova
Gale−Shapley
Zig Zag
SML
1000
100
10
1
10
20
30 40 50 60 70
Taille du problème
80
90 100
Figure 9. Evaluation du temps d’exécution
Casanova a fait l’objet de deux implémentations : l’une à l’aide de la plateforme
multi-agent Jason et l’autre en Java. C’est cette seconde implémentation qui nous a
permis de comparer Casanova avec des méthodes de résolution centralisées ou distribuées. Nos expériences confirment que les solutions obtenues par Casanova sont équitables comme celles obtenues par SML2 (Gelain et al., 2010) et Zig-Zag (Zavidovique
et al., 2005) alors que ces dernières ne sont pas nécessairement stables. De même, on
observe que Casanova améliore la satisfaction globale de la société en explorant des
solutions ignorées par GS (Gale, Shapley, 1962). Enfin, même si le nombre de messages échangés par Casanova est plus important qu’avec DisEGS (Brito, Meseguer,
2005), ce nombre reste linéaire par rapport à la taille du problème.
Casanova
493
À notre connaissance, Casanova est la seule méthode de résolution qui exhibe
simultanément les trois propriétés suivantes :
– décentralisation, i.e. les préférences des individus et le calcul sont distribués ;
– privacité, i.e. les préférences des individus, le statut marital et leur partenaire
ne sont pas divulgués explicitement lors d’échanges avec tout ou partie du système ;
– équité, i.e. la justice entre les communautés est maximisée.
Selon nous, l’équité de la solution et la préservation de la privacité par le système
(la décentralisation en est une condition nécessaire) sont des propriétés essentielles
pour assurer l’acceptation des utilisateurs, quelle que soit l’application retenue.
Nous travaillons actuellement à la preuve théorique de la terminaison et de la correction de notre méthode de résolution. Il serait également nécessaire d’adresser le
problème de l’incomplétude des listes de préférences (problèmes de type SMI).
Le problème du mariage stable est un problème abstrait qui peut être instancié par
une large gamme d’applications pratiques comme l’affectation des projets à des étudiants. On peut penser également au covoiturage qui est un problème d’appariement
entre deux communautés : des conducteurs et des passagers. D’une manière plus générale, le problème SM est un cas particulier du problème d’appariement stable (Stable
Matching Problem). Parmi les extensions possibles, on compte : (i) le problème de colocation (roommate problem) qui consiste à partitionner un ensemble fini d’individus
en couples ou singletons ; (ii) la formation de coalitions où les individus sont partitionnés en fonction de leurs préférences sur les coalitions ; (iii) les marchés sociaux
où des liens peuvent être établis et les individus ont des préférences sur ces liens (voire
sur la structure entière du réseau). Afin de résoudre ce genre de problèmes, l’approche
centrée individu permet d’envisager des algorithmes adaptatifs, anytime et préservant
la privacité des préférences.
Remerciements
Nous remercions les membres du comité de programme des journées francophones
sur les systèmes multi-agents pour leurs commentaires et leurs encouragements.
Bibliographie
Bordini R., Hübner J., Wooldridge M. (2007). Programming multi-agent systems in AgentSpeak
using Jason. Hoboken, New York, United States, John Wiley & Sons Ltd.
Brito I., Meseguer P. (2005). Distributed stable matching problems. In P. van Beek (Ed.),
Principles and practice of constraint programming - CP 2005, vol. 3709, p. 152-166. Heidelberg, Germany, Springer-Verlag.
Brito I., Meseguer P. (2006). Distributed stable matching problems with ties and incomplete
lists. In F. Benhamou (Ed.), Principles and practice of constraint programming - CP 2006,
vol. 4204, p. 675-679. Heidelberg, Germany, Springer-Verlag.
Brito I., Meseguer P. (2007). Distributed forward checking may lie for privacy. In F. Azevedo,
P. Barahona, F. Fages, F. Rossi (Eds.), Recent advances in constraints, vol. 4651, p. 93-107.
494
RIA. Volume 26 – no 5/2012
Heidelberg, Germany, Springer-Verlag.
Dijkstra E., Scholten C. (1980). Termination detection for diffusing computations. Information
Processing Letters, vol. 11, no 1, p. 1-4.
Everaere P., Morge M., Picard G. (2011). Casanova : un comportement d’agent pour l’équité
des mariages préservant la privacité. In Actes des 19ème journées francophones sur les
systèmes multi-agents (JFSMA), p. 191-200. Toulouse, France, Cepaduès.
Gale D., Shapley L. S. (1962). College admissions and the stability of marriage. American
Mathematical Monthly, vol. 69, p. 9-14.
Gelain M., Pini M. S., Rossi F., Venable K. B., Walsh T. (2010). Local search algorithms
on the stable marriage problem: Experimental studies. In Proceedings of 19th european
conference on artificial intelligence (ECAI), p. 1085-1086. Amsterdam, NL, IOS Press.
Glize P., Picard G. (2011). Self-organisation in constraint problem solving. In G. Serugendo,
M.-P. Gleizes, A. Karageorgos (Eds.), Self-organizing software: From natural to artificial
adaptation, p. 347-377. Heidelberg, Germany, Springer-Verlag.
Knuth D. (1971). Mariage stables. Montréal, Canada, Les Presses de l’Université de Montréal.
Mitchell T. (1997). Machine learning. New York, NY, USA, McGraw-Hill.
Morge M., Mancarella P. (2010). Assumption-based argumentation for the minimal concession
strategy. In Proceedings of workshop on argumentation and multi-agent systems (ArgMAS),
vol. 6057, p. 114-133. Heidelberg, Germany, Springer-Verlag.
Moulin H. (2003). Fair division and collective welfare. Cambridge, Massachusetts, USA, MIT
Press.
Rao A. (1996). AgentSpeak(L): BDI agents speak out in a logical computable language. In
R. van Hoe (Ed.), Proceedings of 7th european workshop on modelling autonomous agents
in a multi-agent world (MAAMAW). New York, USA, Springer-Verlag.
Rosenschein J., Zlotkin G. (1994). Rules of encounter: designing conventions for automated
negotiation among computers. Cambridge, Massachusetts, USA, MIT Press.
Roth A. E., Oliveira Sotomayor M. A. (1990). Two-sided matching; a study in game-theoretic
modeling and analysis. Cambridge, England, Cambridge University Press.
Schelling T. (1978). Micromotives and macrobehavior. New York, USA, Norton & Co.
Yokoo M., Durfee E., Ishida T., Kuwabara K. (1998). The distributed constraint satisfaction
problem: Formalization and algorithms. IEEE Transactions on Knowledge and Data Engineering, vol. 10, p. 673–685.
Zavidovique B., Suvonvorn N., Seetharaman G. S. (2005). A novel representation and algorithms for (quasi) stable marriages. In Proceedings of 2nd international conference on
informatics in control, automation and robotics (ICINCO), p. 63-70. Barcelona, Spain,
INSTICC Press.