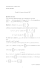Théorème de Molien

DÉVELOPPEMENTS POUR L’AGRÉGATION EXTERNE
Théorème de Molien 1
Leçons : 101, 124, 142, 104, 106, 107, 140, 151, 152, 154, 155
Très librement inspiré de [Lei], page 95
Théorème
On note M = C [ X1 , . . . , Xn ] et Mk ⊂ M le sous-espace des polynômes homogènes de degré k.
Soit G un sous-groupe fini de GLn ( C).
M
→
M
Pour g ∈ GLn (C), on définit : σg : , où X = ( X1 . . . Xn ) est le vecteur-ligne des
P( X ) 7→ P( Xg)
indéterminées.
Alors σg induit un automorphismesur chaque Mk , on note mk = dim Mk et mk ( G ) = dim MkG , où
MkG = P ∈ Mk ∀ g ∈ G, σg ( P) = P .
Et on a l’égalité dans C[[ Z ]] : 2
1
#G
∞
1
= ∑ mk ( G ) Z k
det(Id − gZ )
g∈ G
k =0
∑
Démonstration :
Étape 1 : σg induit un automorphisme sur chaque Mk .
Soient g, g0 ∈ GLn (C), on a : σgg0 = σg σg0 et σId = Id, donc σg ∈ GL( M).
Soit k ∈ N, on remarque que l’image par σg d’un monôme de degré total k est un polynôme homogène de degré k.
Par linéarité, on en déduit que σg ( Mk ) ⊂ Mk .
Or σg M est injectif car σg l’est et dim Mk < ∞, donc σg M ∈ GL ( Mk ).
k
k
∞
1
Étape 2 : Montrons l’égalité de séries formelles
= ∑ tr σg M Z k pour g ∈ G.
k
det(Id − gZ )
k =0
Par le théorème de Lagrange, on a : g#G = Id.
Or X #G − 1 est scindé à racines simples, donc g est diagonalisable.
Donc ∃u ∈ GLn (C), g = udu−1 , avec d = diag(λ1 , . . . , λn ). Ainsi, σg M et σd
k
Mais aussi :
Mk
sont semblables, d’où tr σg
1
1
=
=
det(Id − gZ )
det(Id − dZ )
où on a posé vk =
∑
r1 ,...rn ∈N
r1 +...+rn =k
Or :
σd
r
λ11
Mk
= tr σd
Mk
1
n
n
∏ 1 − λi Z
i =1
=∏
.
∞
∞
∑ λik Zk = ∑ vk Zk
i =1 k =0
k =0
. . . λrnn .
r
r
r
X11 . . . Xnrn = (λ1 X1 )r1 . . . (λn Xn )rn = λ11 . . . λrnn X11 . . . Xnrn
Mk
1. Le jury veut que vous soyez capables d’en parler si vous présentez ce développement ! Un lien vers un document rédigé
par Arnaud S TOCKER pour vous donner une idée de ce à quoi ce théorème peut servir.
2. Même si je le déconseille parce qu’on n’a pas besoin d’arguments analytiques dans ce développement, quand on veut
travailler avec des séries entières, on doit ajouter le lemme suivant, qui justifie que toutes les séries entières en jeu ont des
rayons de convergence supérieurs ou égaux à 1 :
Lemme
Si |z| < 1, alors
1
1−z
∞
n
=
∑ mk zk .
k =0
En effet, Mk admet pour base X1r1 . . . Xnrn
Et pour |z| < 1 :
1
1−z
∞
n
Florian L EMONNIER
=
∑ zk
k =0
!n
r1 ,...,rn ∈N
r1 +...+
rn =k
∞
=
∑

k =0

; donc mk = dim Mk = # {(r1 , . . . , rn ) ∈ Nn |r1 + . . . + rn = k}.

∑
r1 ,...,rn ∈N
r1 +...+rn =k
 k
1
z =
1
∞
∑ mk zk .
k =0
Diffusion à titre gratuit uniquement.
ENS Rennes – Université Rennes 1
DÉVELOPPEMENTS POUR L’AGRÉGATION EXTERNE
r
Et comme X11 . . . Xnrn
Donc
r1 ,...,rn ∈N
r1 +...+rn =k
∞
1
= ∑ tr σg
det(Id − gZ )
k =0
est une base de Mk , on obtient : vk = tr σd
Mk
Mk
.
Z k pour tout g ∈ G.
Étape 3 : Concluons.
Lemme
Soit V un C-ev de dimension n < ∞, ϕ : G → GL(V ) un morphisme de groupes et G un groupe fini.
On note V G = {v ∈ V |∀ g ∈ G, ϕ( g)(v) = v}.
On a alors :
1
tr( ϕ( g)) = dim V G
#G g∑
∈G
Démonstration :
1
On pose pG =
#G
∑
ϕ( g). On a : ∀h ∈ G, ϕ(h) ◦ pG =
g∈ G
1
#G
Donc ∀v ∈ V, ∀h ∈ G, ϕ(h) ( pG (v)) = pG (v), donc pG (V )
1
Soit v ∈ V G , pG (v) =
v = v et donc pG (V ) = V G .
#G g∑
∈G
∑
ϕ(h) ◦ ϕ( g) =
g∈ G
⊂ VG.
1
#G
∑
ϕ(hg) = pG .
g∈ G
Soit v ∈ V, pG ( pG (v)) = pG (v), car pG (v) ∈ pG (V ) = V G et donc pG est un projecteur.
1
tr( ϕ( g)).
Dès lors : dim V G = rg pG = tr pG =
#G g∑
∈G
→ GL ( Mk )
est un morphisme de groupes.
7→ σg M
k
1
Par le lemme, on a : dim MkG = mk ( G ) =
tr
σ
.
g
Mk
#G g∑
∈G
Par conséquent :
Ici, ∀k ∈
1
#G
N, σ(k)
∑
g∈ G
G
: g
1
1
=
det(Id − gZ )
#G
∞
∑ ∑ tr
g ∈ G k =0
σg
Mk
k
Z =
∞
∑
k =0
1
#G
∑ tr
g∈ G
σg
Mk
∞
!
Z
k
=
∑ mk ( G ) Z k
k =0
Références
[Lei] É. L EICHTNAM – Exercices corrigés de mathématiques Polytechnique-ENS (Tome algèbre et géométrie),
Ellipses, 1999.
Florian L EMONNIER
2
Diffusion à titre gratuit uniquement.
ENS Rennes – Université Rennes 1